Math 121 - Calculus for Biology I
Spring Semester, 2004
Logistic Growth - Worked Examples
San Diego State University -- This page last updated 18-Mar-04
|
|
Math 121 - Calculus for Biology I |
|
|---|---|---|
|
San Diego State University -- This page last updated 18-Mar-04 |
![]()
Logistic Growth - Worked Examples
These examples expand on the qualitative techniques for analyzing the logistic growth model
Examples for Analysis of the Logistic Growth Model
Example 1:
Consider the discrete logistic growth model
Solution:
For equilibria, substitute Pe for Pn and Pn+1 into the discrete logistic growth model
Pe = 1.3Pe - 0.0001Pe2
0 = 0.3Pe - 0.0001Pe2 = Pe (0.3 - 0.0001Pe)
Pe = 0 and
0.3 - 0.0001Pe = 0 or Pe = 3000
f1'(0) = 1.3 > 1
f1'(3000) = 1.3 - 0.6 = 0.7 < 1
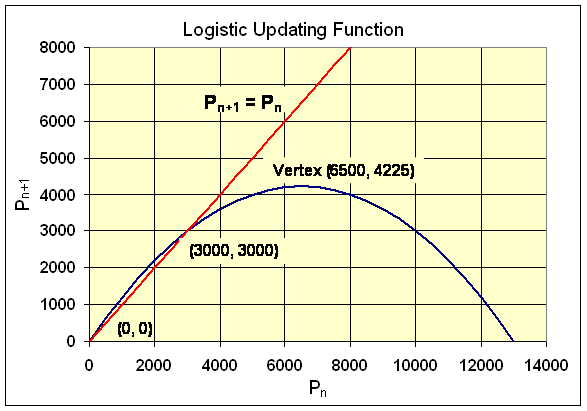
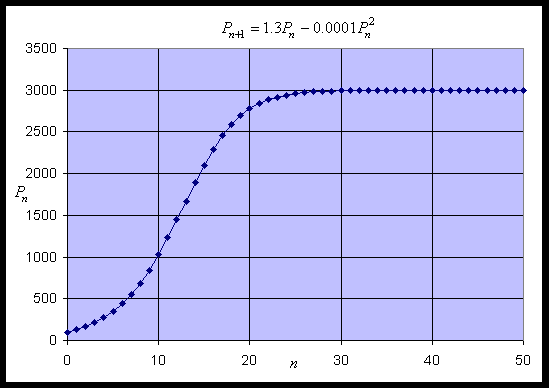
Example 2: Modify the example above and consider the discrete logistic growth model
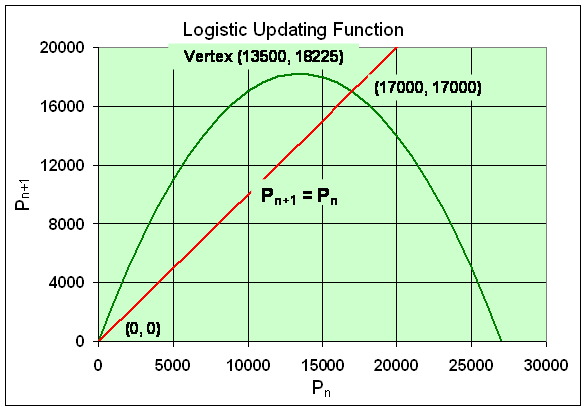
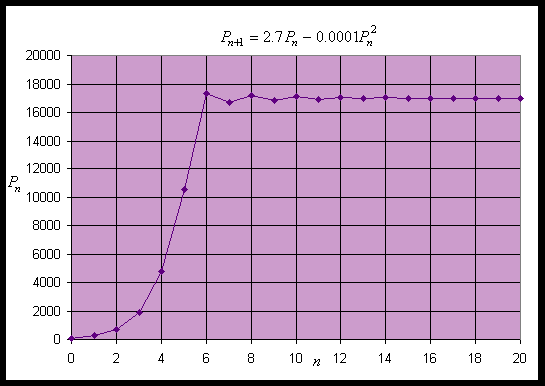
Solution: Substitute Pe for Pn and Pn+1 into the discrete logistic growth model
Pe = 2.7Pe - 0.0001Pe2
0 = 1.7Pe - 0.0001Pe2 = Pe (1.7 - 0.0001Pe)
Pe = 0
Pe = 17000
f2'(0) = 2.7 > 1
f2'(17000) = 2.7 - 3.4 = -0.7
Simulation of this model with an initial value of P0 = 100 and 20 iterations
Example 3: Another change in the discrete logistic growth model gives
Solution: Substitute Pe for Pn and Pn+1 into the discrete logistic growth model
Pe = 3.2Pe - 0.0001Pe2
0 = 2.2Pe - 0.0001Pe2 = Pe (2.2 - 0.0001Pe)
Pe = 0
Pe = 22000
f3'(0) = 3.2 > 1
f3'(22000) = 3.2 - 4.4 = -1.2
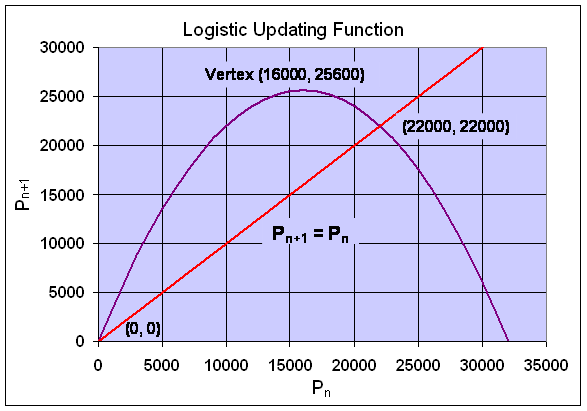
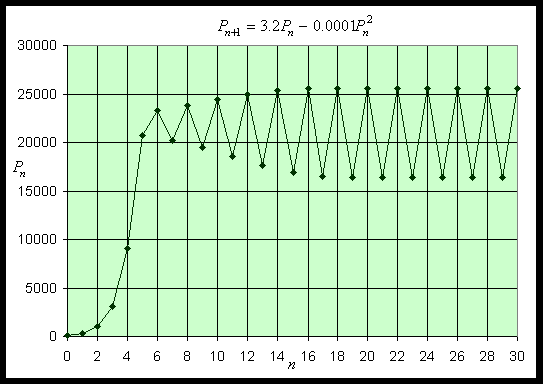
Example 4 (Growth Rate Function for Logistic Model):
where n is measured in hours
a. Assume that p0 = 500 and find the population for the next three hours, p1, p2, and p3.
b. Find the p-intercepts and the vertex for
Sketch a graph of g(p).
c. By finding when the growth rate is zero, determine all equilibria for this model and find the stability of the equilibria.
Solution:
a. The first three iterations are
p2 = 524 + 0.05(524)(1 - 0.0001(524)) = 549,
p3 = 549 + 0.05(549)(1 - 0.0001(549)) = 574.
b. The p-intercepts are found by solving
g(p) = 0.05 p(1 - 0.0001p) = 0,
Thus,
p = 0 or
p = 10,000.
p = 5,000
g(5000) = 0.05(5000)(1 - 0.0001(5000)) = 125
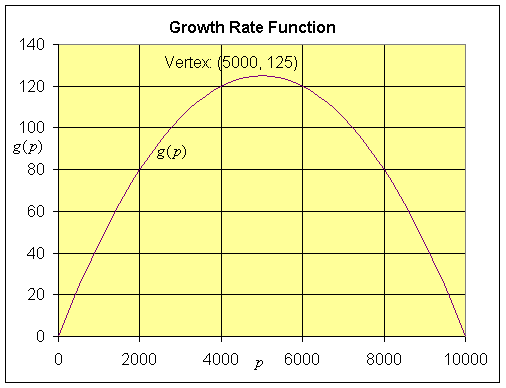
c. From the graph above, it is clear that the growth rate is zero at 0 and 10,000, so the equilibria occur at
pe = 0 and 10,000.
pn+1 = f(pn) = 1.05 pn - 0.00005pn2.
f '(pn) = 1.05 - 0.0001pn.
Example 5 (Stability of the Malthusian Growth Model):
Solution:
Pe = (1 + r)Pe
rPe = 0 or Pe = 0
The discrete dynamical model for this population model is
where n is measured in generations.
a. Assume that p0 = 100 and find the population for the next three generations, p1, p2, and p3.
b. Find the p-intercepts and the vertex for g(p) and sketch a graph of g(p).
c. By finding when the growth rate is zero, determine all equilibria for this model.
Solution:
a. The next three generations are
p2 = 154 + 0.71(154) - 0.001(154)2 - 7 = 233,
p3 = 233 + 0.71(233) - 0.001(233)2 - 7 = 337.
b. The growth function satisfies
g(p) = 0.71 p - 0.001p2 - 7
g(p) = -0.001(p2 - 710p + 7000)
g(p) = -0.001(p - 10)(p - 700).
The p-intercepts satisfy g(p) = 0, so
p = 10 or p = 700.
The vertex occurs halfway between the p-intercepts, so p = 355 and
g(355) = -0.001(345)(-345) = 119.
The maximum growth occurs when the population is 355 with a maximum growth of 119 individuals/generation.
The graph of g(p) is shown below showing the p-intercepts at p = 10 and 700 and the vertex.
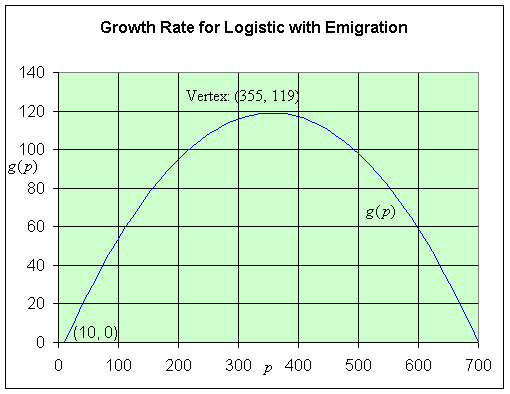
c. From the graph above, it is clear that the growth rate is zero at p = 10 and 700, so the equilibria occur at pe = 10 and 700.
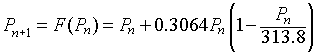
Pn+1 = (1.3835 - 0.0155n)Pn.
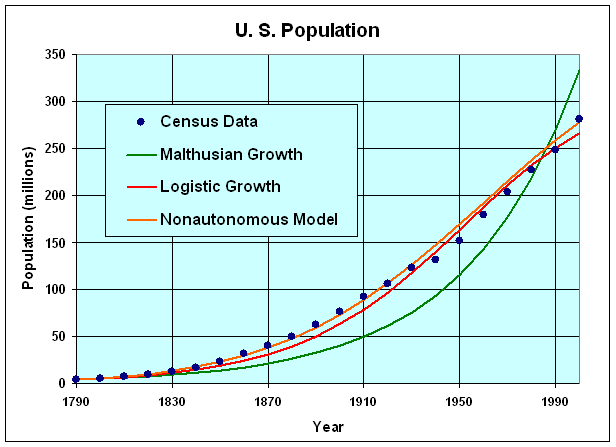
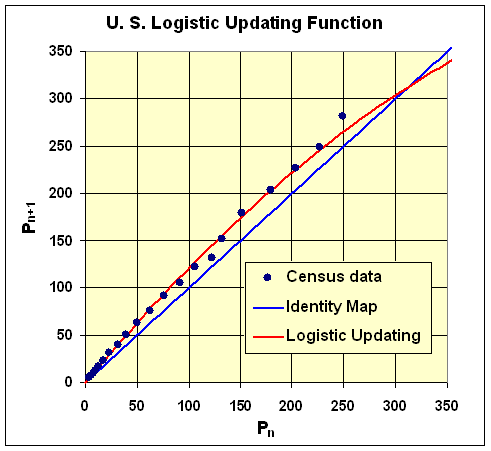
F '(P) = 1.3064 - 0.00195P.