Math 121 - Calculus for Biology I Fall Semester, 2003 Discrete Malthusian Growth
	© 2001, All Rights Reserved, SDSU & Joseph M. Mahaffy San Diego State University -- This page last updated 14-Oct-03

 Discrete Malthusian Growth

Outline of Chapter

1. Population of the United States
2. Discrete Malthusian Growth
3. Applet for U. S. Population Growth
4. Example of Malthusian Growth
5. Worked Examples
6. Improved Malthusian Growth Model
7. References

Discrete Dynamical systems examine events at regular time intervals.

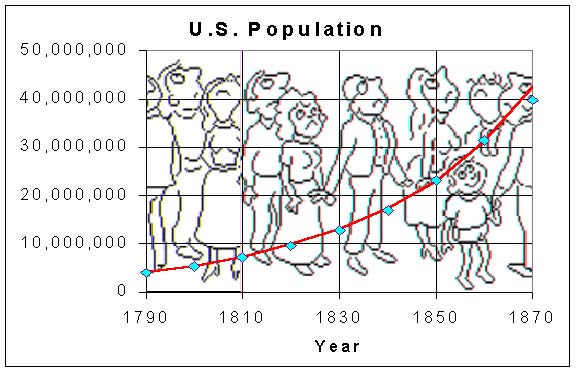
Population of the United States

• United States census occurs every 10 years
• The census is used for budgeting federal payments and representation in Congress
• Controversy landed in the Supreme Court
  • Republicans wanted a strict interpretation of the Constitution, knowing that a direct head count always undercounts minorities and the poor, who vote predominantly Democratic
  • Democrats claimed that the Constitution framers wanted an accurate count of the populace, so that modern statistical methods should be employed, giving them the advantage
  • The Supreme Court came down in the middle pleasing neither party and saying that the Constitution requires a head count, which will be used for allocating Congressional seats and districting, while the more accurate statistical count may be used for apportioning the money for Federal funding
• Accurately predicting demographic data are important for planning communities in the future
• Calculations for the future populations uses a mathematical model
• Current models are quite sophisticated, but we begin with the basic models

The growth rate for the decade of 1790-1800

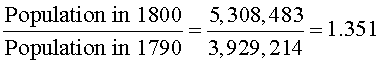
Thus, the growth rate for this decade is 35.1%

The javascript below finds the growth rate for any decade in the history of the U. S.

• The growth rates for decades following 1790, 1800, and 1810 are 35.1%, 36.4%, and 33.1%, respectively
• This averages 34.9% per decade
• This growth rate remains almost constant until 1860
• Suggests using a model with a constant growth

• Simplest mathematical model says that the population in the next decade is equal to the current population plus the current population times the average growth rate, r
• Begin with some starting population, say in 1790
• Future populations are predicted at each decade (discrete time intervals) by starting with this initial given population, then finding the next population from the previous population by multiplying by (1 + r)
• This sequence of predicted populations is based solely on the population from the preceding decade
• With the population of 3,929,214 in 1790, an estimate of the population in 1800 is

• Notice that this prediction is less than 8,000 off the actual census value or a 0.15% error

• Repeat this process to predict each of the succeeding census populations up until 1860 (a period where the growth rate remains fairly constant).
• Below is a table of this constant growth model applied to the census up until 1870

• The error remains small until 1870 because of the fairly constant rate of growth
• Most of the predicted populations are a little high, especially in 1870, suggesting that throughout the 19^th century the growth rate declined
• The declining growth rate is a general trend that we observe for the U. S. (This is studied in the next improved model below.)

• Between 1860 and 1870, the Civil War occurred, which is one cause of the dramatic decline in the rate of growth of the population in the U. S
• The shift from the primarily agricultural society to the industrial revolution is more significant in causing the decline in the rate of growth
• We will study more about crowding effects in the next lecture section
• Below is a graph of the population model and the data from the table above

• This model is limited to a range of dates where the growth rate remains relatively constant
• Extending this model until 1920 or 1970 produces the census values of 192,365,343 and 859,382,645, respectively. (These estimates are 82% and 323% too high.)
• The growth rate in 1920 is 15% and drops to only 13% in 1970
• The lowest growth rate of 7.2% occurred during the Great Depression (between 1930 and 1940)
• This simple model is clearly limited

Discrete Malthusian Growth

• Let the integer n represent the number of decades after 1790
• Define P_n to be the population for the n^th decade after 1790 (with P₀ again representing the population in 1790)
• The population for one decade is estimated by using the population from the previous decade and adding to it the average percent growth multiplied by the population from the previous decade
• The mathematical model based on this description is given by:

where r is the average growth rate

• This equation is the Discrete Malthusian Growth model (named after the work of Thomas Malthus (1766-1834))
• This is a special example of Discrete Dynamical systems or Difference equations
• Population models using difference equations are commonly used in Ecological modeling
• The Malthusian growth model states that the population of the next generation is simply proportional to the population in the current generation, which is what is written in the equation above.

Solution of Discrete Malthusian Growth Model

• Few discrete models that have an explicit solution
• It is easy to solve the discrete Malthusian growth model

• The general solution of this model is given by

• This shows why Malthusian growth is also known as exponential growth
• The solution to the model is an exponential function with a base of 1+ r and power n representing the number of iterations after the initial population is given

Applet for Malthusian Growth for the U. S. population

• The Malthusian growth model assumes a constant growth rate, so is unlikely to do well predicting the population over long periods of time where growth rate varies
• Because of the exponential nature of the Malthusian growth model, this model can rapidly diverge from the actual population

 sourcecode for growth6g - Alternate link

• If you choose the interval from 1790 to 1860 with a growth rate of r = 0.349, then the Malthusian growth model matches quite well
• If you try to fit the entire range of data from 1790 to 1990, then you will find no value of r that allows the Malthusian growth model to fit the data
• The average growth rate of 23.5% has the Malthusian growth model match the data at 1790 and 1990, but fails to do well for the intermediate data points
• By making r into a function which depends on either time or population or both, then we can see how this model can be improved
• For more information on human population growth visit the UN website on population

Example of Malthusian Growth

Suppose that a population of yeast, satisfying Malthusian growth, grows 10% in an hour. If the population begins with 100,000 yeast, then find the population at the end of 4 hours. How long does it take for this population to double?

Solution:

• The population of yeast satisfies the equation

• The population after one hour is P₁ = 1.1P₀ = 110,000
• After two hours, P₂ = 1.1P₁ = (1.1)²P₀ = 121,000
• After 4 hours,

• For the population to double, it must reach 2P₀ = 200,000
• Solve

• By taking the logarithms of both sides we have

Worked Examples for Malthusian Growth.

Improved Malthusian Growth Model

• We extend the Malthusian Growth model to include time varying reproduction rates
• Compare the two models on how they do in predicting the 2000 census
  • The discrete Malthusian growth model using the average growth rate over all the data
  • An improved modified model that uses a time dependent growth rate, which is acquired by fitting a straight line through the growth rate data

• The general discrete dynamical population model is given by

where f is a function depending only on the population P at time t_n

• This difference equation is said to be autonomous as it does not have a temporal or time dependence
• A more general difference equation is given by

which is a nonautonomous difference equation.

• The average growth rate over all the census dates from 1790 to 1990 is

• The discrete Malthusian growth model is

• This growth rate is too low for the early years, and too high for later years
• If we use this model to predict the population in the year 2000 starting with the population in 1790, then from the solution of the Malthusian Growth model above we have that the year 2000 is 21 decades after 1790, so with P₀ = 3,929,214, then

• This prediction is clearly too high (about 16% too high).

• A modified time dependent growth rate is found by fitting a line through the data from 1790 to 1990
• The best fit to these growth rate data, along with the average growth rate, is seen in the graph below:

• The best fit to the growth rate data from 1790 to 1990 is given by the equation

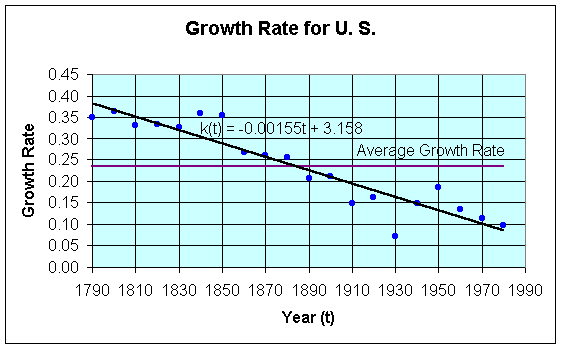
where t is the date of the census.

• The resulting modified nonautonomous difference equation is

where t_n = 1790 + 10n and n is the number of decades after 1790

• The model can be written

  P_n+1 = (1.3835 - 0.0155n)P_n

• The graph below gives a comparative study of these two models
• The Malthusian Growth model performs poorly as noted above because the growth rate varies too much over the time interval being considered
• The Nonautonomous Discrete Malthusian Growth model matches the data quite well though runs a bit high after the severely depressed population growth during the Great Depression

• Note that computing the population using the Nonautonomous Malthusian Growth model is more complicated than the simpler Discrete Malthusian Growth model
• We have the general solution for the simpler model as shown by the computation above where obtaining the population in 2000 requires only knowing the population in 1790, then raising 1.2342 to the 21^st power
• The computation for the Nonautonomous Malthusian Growth model requires finding the solution at each decade to proceed to the next decade

• The Nonautonomous Malthusian Growth model starts with the population in 1790 (= 3,929,214), then (1 + k(1790)) is computed (=1.3835) and multiplied by the population in 1790 (=3,929,214) to give the population for 1800 (= 1.3835 x 3,929,214 = 5,436,068)
• For the second decade, the predicted population in 1800 (= 5,436,068 ) is multiplied by the computed value for 1 + k(1800) (=1.3680), to arrive at the new prediction for the population of 1810 (= 1.3680 x 5,436,068 = 7,436,540 )
• Below is a table showing the calculations needed to get the predicted 2000 census, along with the errors as the model iterates

• We see that the Nonautonomous Malthusian Growth model predicts a 2000 census of 278,244,477, which is only slightly lower than the actual value found by the U. S. census bureau
• However, you can see that generating these numbers required significantly more effort than the simple Discrete Malthusian Growth model

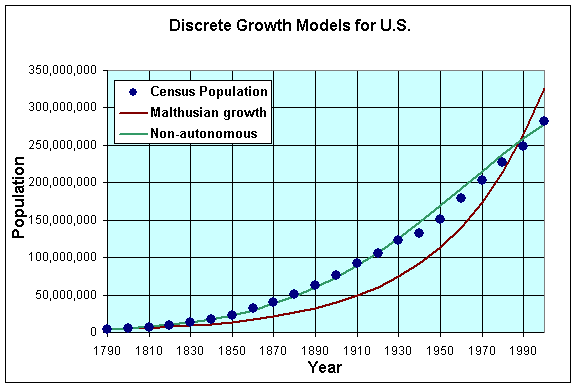
[1] Statistical Abstracts of the United States (1993) 113 ^th ed., U. S. Department of Commerce, Bureau of the Census, Washington, DC.