The most common technique for fitting a straight line to data is the linear least squares best fit or linear regression. (The term regression comes from a pioneer in the field of applied statistics who gave the least squares line this name because his studies indicated that the stature of sons of tall parents reverts or regresses toward the mean stature of the population.)

Finding the C period for E. coli

• Escherichia coli can divide every 20 minutes
• Genetic material is organized on a large loop of DNA (3,800,000 base pairs)
• Replicates in both directions, starting at oriC and terminating about halfway around the loop
• Figure above right shows DNA
• Bacteria (prokaryotes) cell cycle differs from eukaryotic organisms
• Time for the DNA to replicate is the C period
• Time for the two loops of DNA to split apart, segregate, and form two new daughter cells is the D period
• The C period is 35-50 min, and the D period is over 25 min - longer than the 20 min cell cycle
• Up to 8 oriCs in a single E. coli

Pulse Labeling Experiment

• In E. coli, a pulse label of radioactive thymidine is given to determine the length of the C period
• Below are data from the laboratory of Professor Judith Zyskind (SDSU)
• E. coli are treated with drugs at t = 0 stopping replication and division
• Radioactive emissions, c in counts/min (cpm) measured after pulse labels given at various times following the treatment

 
• Estimate the C period using a simple linear model,

 
• Actual modeling process uses integral Calculus
• The t-intercept gives an approximate value to the C period
• Find the slope, a, and the intercept, b, that minimizes value of J(a,b), giving the least squares best fit to the data. The t-intercept (when c = 0) occurs at t = -b/a.

The least squares best fit to the data is given by the line

The t-intercept is 42.7, so this model estimates the C period as 42.7 min.

Least Squares Best Fit

• The least squares best fit of a line to data (also called linear regression) is the best line through a set of data.
• Consider a set of n data points: (x₁, y₁), (x₂, y₂), ... , (x_n, y_n).
• Select a slope, a, and an intercept, b, that results in a line that in some sense best fits the data

• The least squares best fit minimizes the square of the error in the distance between the y_i values of the data points and the y value of the line.
• It depends on selection of the slope, a, and the intercept, b.
• The error between each of the data points and the line is

  e_i = y_i - y(x_i) = y_i - (ax_i + b), i = 1,...n.

• Define the absolute error between each of the data points and the line as

• The error e_i varies as a and b vary.

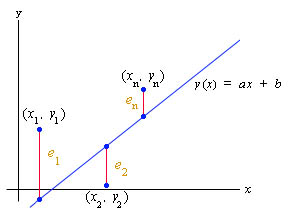
The least squares best fit is found by finding the minimum value of the function

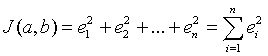
The technique for finding the exact values of a and b uses Calculus of two variables. The formulae for finding a and b can be found in any book on statistics. A hyperlinked appendix is provided to give you these formulae, but this is only provided for completeness and not as part of this course. You will learn much more about this topic in your Biostatistics course (Biology 215).

Worked Example:

• The line, which minimizes the error for the C period in the data above, is given by the formula:

• The first datum point is t = 10 and c = 7130.
• The model predicts c(10) = 6900, so the error between the experimental and the theoretical value is

• Similarly,

• The sum of the squares of these errors is

Hyperlinked section to Worked Examples related to the homework problems.

Juvenile Height Revisited

• Recall the example from the linear lecture notes on the average height of a child.
• In the applet below, adjust the slope, m, and the intercept, b, to find the minimum value of J(m,b).
• This is the least squares best fit to the data.

Alternate Image - Alternate link

The resulting least squares best fit to the data is given by the line

The square of the error is found to be

Calculating Percent and Relative Error

There are a number of techniques for computing the error in a measurement. Let X_e be an experimental measurement and X_t be the theoretical value. In this course, most often X_e will be the value from a model that we want to test, while X_t will be results from actual data that we acquire and assume is true. The actual error is simply the difference between the experimental (or model) value and the theoretical (or actual data) value. So the actual error is given by

Often we only need the magnitude of the error or as in the case of the least squares best fit the error is squared making the sign of the error irrelevant. In this case, we use the absolute error, which is simply the absolute value of the difference between the experimental (or model) value and the theoretical (or actual data) value. So the absolute error is given by

More often the error is presented as either the relative error or percent error. This error allows a better comparison of the error between data sets or within a data set with large differences in the numerical values. The relative error is the difference between the experimental (or model) value and the theoretical (or actual data) value divided by the theoretical (or actual data) value, so

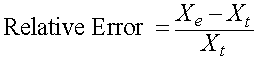
The percent error is closely related to the relative error, except that the value is multiplied by 100% to change the fractional value to a percent, so

References:

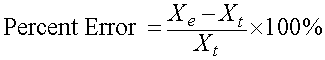
[1] J. L. Ingraham, O. Maaloe, and F. C. Neidhardt, Growth of the Bacterial Cell, Sinauer Assoc., Inc., Sunderland, MA, 1983.

[2] Ruth Kavenoff and Brian Bowen, Bluegenes #1, Designergenes Posters, ltd., 1989.

[3] F. C. Neidhardt, Escherichia coli and Salmonella typhimurium: Cellular and Molecular Biology, American Society of Microbiology, Washington, D.C., 1987.