Math 121 - Calculus for Biology I
Spring Semester, 2009
Logistic Growth and Nonlinear Dynamical Systems
San Diego State University -- This page last updated 11-May-09
|
|
Math 121 - Calculus for Biology I |
|
|---|---|---|
|
|
San Diego State University -- This page last updated 11-May-09 |
|
Discrete Logistic Growth Model
In an earlier section we studied the Discrete Malthusian growth model, which showed exponential growth. This model is appropriate for early phases of population growth for most animal populations. However, as a population grows, it encounters crowding pressure due to many factors such as toxic build up or space and resource limitation.
In 1913, Carlson [1] studied a growing culture of yeast.
Below is a table of the population for these yeast at one hour intervals. We
would like to develop a mathematical model to describe the growth of this culture.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
There are two standard forms of the discrete population models. The first form uses a growth function, G(pn).
pn+1 = pn + G(pn).
This form is stating that the population at the next time interval (n+1) is equal to the population at the current time interval (n) plus whatever net growth occurred because of the current population, G(pn), during the specific tiime interval.
An alternate form, which gives the general discrete dynamical system, is given by the
This is an iterative map where the population at the (n + 1)st time depends on the population at the nth time. The function F(p) is called the updating function as it produces the next population in an iterative scheme. A graph of the updating function has the (n + 1)st generation on the vertical axis, while the nth generation is on the horizontal axis.
It is clear that the population of yeast in the table above does not satisfy a Malthusian growth, which has a linear updating function and grows exponentially without bound. The next obvious addition to the updating function is the addition of a quadratic term, which should be negative to reflect a decrease in the growth of a population due to crowding effects. This is the Logistic Growth model and can be written:
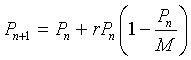
This equation has the Malthusian growth model as seen before with the additional term -rPn2/M. The parameter M is called the carrying capacity of the population.
The behavior of the Logistic growth model is substantially more complicated than that of the Malthusian growth model. There is no exact solution to this discrete dynamical system. The ecologist Robert May (1974) studied this equation for populations and discovered that it could produce very complicated dynamics. In its simplest form the Logistic growth model can be written:
where the parameter m varies between 0 and 4. For a good description of this model complete with Java applet simulations see the website of B. Fraser.
The graph below shows a plot of pn+1 vs. pn
from the table above. (This is accomplished by plotting the population from
one time against the population from the previous time. For example, the first
two points are (9.6, 18.3) and (18.3, 29.0).) The graph of the
data is fit applying Excel's polynomial fit with trendline, using a quadratic
passing through the origin, and is shown below. The graph of the line
pn+1 = pn (the
identity map) is also shown, and
its importance for studying discrete dynamical models will be discussed later.
This equation becomes the updating function.
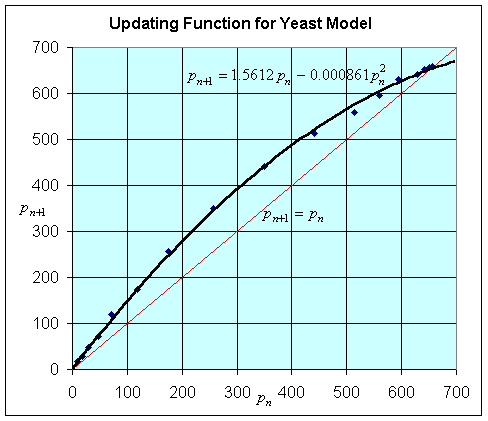
Our discrete logistic growth model for the yeast experiment above is given by
Below is a simulation showing both the data and the model, assuming that we begin with p0 = 9.6. As we can see, the model does a fairly reasonable job of simulating the data from this fairly simplistic model.
Qualitatively, we see the same initial roughly exponential growth, then both models seem to level off at approximately the same value. This is the carrying capacity of the population. The equation above shows r = 0.56 and r/M = 0.000861, so M = 650.4. This is clearly a little low based on the original table. Furthermore, the model is shifted in time, not rising as soon as the original data.
This section extends our study of discrete dynamical equations to nonlinear functions in order to find what can be learned about their qualitative behavior. The linear discrete dynamical models were introduced before the sections on differentiation showing the modeling of populations with Malthusian growth and other linear models, such as one for breathing. As noted above, there is no general solution for the logistic growth model. However, we would like to learn more about this very important model from population biology. Here we introduce the key steps for studying the qualitative behavior of discrete dynamical equations.
Consider the general discrete dynamical equation:
The first step in any analysis of a discrete dynamical equation is finding equilibria, which is simply solving an algebraic equation. An equilibrium point of a discrete dynamical system is a point where there is no change in the variable from one iteration to the next. Mathematically, this occurs whenever there is a solution to
Graphically, this is when f(Pn) crosses the line Pn+1 = Pn, the identity map, which is one reason why this line was shown above.
Consider the original discrete Logistic equation listed above with r > 0. The equilibria are found by solving:
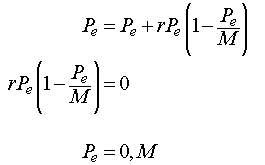
Thus, the equilibria for the Logistic growth model are either the trivial solution 0 (no population) or the carrying capacity M.
Other Behavior of the Logistic Growth Model
Before learning more mathematical tools for studying the discrete logistic growth model, it is useful to examine some of the wealth of behaviors that are possible for this model. Below we present an applet that shows simulations of the logistic growth model for various choices of r and M. You can vary the values of these parameters and see how the simulation changes over the first 50 iterations.
Robert May (1974) demonstrated that the discrete Logistic growth model could display very complicated dynamics.Watch what happens in the applet above as we choose different values of r. For example, try the values r = 0.5, 1.8, 2.3, and 2.65. (Note that the solution of the discrete Logistic equation only gives solutions at the integer values of n, so the connecting lines are only drawn to help visualize the behavior of the system.) The first value of r shows the curve smoothly ascending to carrying capacity of 1000. The second value of r has the population ascend and actually overshoot 1000, then oscillates about 1000, getting closer to the carrying capacity as n increases. In both of these cases, the equilibrium population of 1000 is said to be stable. When r = 2.3, the solution oscillates about 1000, taking on the values of approximately 690 and 1180. This solution is said to have a period of 2. The last case shows the population oscillating almost randomly about 1000. This last situation could have either a very high period of oscillation or actually be chaotic. See what happens when you change the value of M.
Stability of the Logistic Growth Model
The applet above showed that the behavior of the discrete logistic model changes very dramatically as the parameter r varies. We would like to have some mathematical tools that help us predict some of these behaviors. If we write the discrete logistic growth model
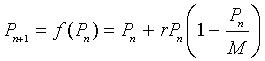
then the derivative of the function f(P) proves to be a valuable tool for determining the behavior of the discrete dynamical system near an equilibrium point.
The discrete logistic growth model, as given by the equation above, has two equilibria,
It is easy to see that the derivative of f(P) is given by
At Pe = 0, the derivative satisfies
which for r positive always results in solutions growing away from this equilibrium. (If r is a negative number between -1 and 0, then the solution of the discrete logistic growth model decays to 0 or the population goes to extinction.)
The more interesting behavior occurs around the second equilibrium, Pe = M. Below is a summary of the types of behavior that are observed for a discrete dynamical system near an equilibrium, Pe. (In all of the descriptions below, we are assuming that the simulation begins "near" the equilibrium value.)
Behavior of the Discrete Dynamical Model near an Equilibrium
Returning to the logistic growth model, we can evaluate the derivative at the larger equilibrium, Pe = M. From the formula for the derivative, it is easy to see that
From our list of behaviors above, it is follows that
There are Worked Examples available to help you understand the material.
In the section on linear discrete dynamical models, we introduced a more geometric way to visualize these dynamical systems, cobwebbing. The website of B. Fraser shows this cobwebbing for the logistic growth model in a nice applet. The updating function, f(pn), is graphed with the identity map, pn+1 = pn on a single graph with the vertical axis being pn+1 and the horizontal axis being pn. The idea is that you start at any p0, then go vertically to p1 = f(p0). Next you go horizontally to the identity map to locate p1 on the horizontal axis. From there you find p2 by going vertically to p2 = f(p1). This process is repeated to generate the cobweb of points by this discrete dynamical system. The sequence of points on the horizontal axis form the solution set generated by the discrete dynamical system. The graphical representation allows you make some projections of the behavior of the system. Below is a diagram showing several steps in the cobwebbing scheme for the quadratic map
[1] T. Carlson Über Geschwindigkeit und Grösse der Hefevermehrung in Würze. Biochem. Z. 57: 313-334, 1913.