1. Logistic Growth Model
2. Bernoulli's Method
3. References

This section provides an analytical solution to the Logistic growth model. The analytical solution makes fitting parameters to the model easier to the data in the Gause experiments. Details on fitting this solution to the data along with a qualitative analysis of the Logistic growth model are developed on the webpage found through this hyperlink.

Logistic Growth Model

Our study of competition models were motivated by some classical experiments on yeast by Gause [1]. The initial growth was exponential and followed a model for Malthusian growth. A closer analysis of the data on the monocultures showed that the growth slowed as the population density increased until the populations leveled off at a carrying capacity of the culture. This behavior required the addition of another term to the Malthusian growth model, which resulted in the Logistic growth model. The qualitative analysis of the this equation provided relatively easy techniques for determining the equilibria and the general behavior of the model. However, the qualitative analysis falls short on helping determine the best fitting parameters to match the model to the data. An analytical solution makes fitting the parameters in the differential equation simpler.

The logistic growth model is given by the following differential equation:

In this section, we show one method for solving this differential equation. The logistic growth model is clearly a separable differential equation, but separating variables leaves you with an integral that requires integration using partial fractions decomposition and then still requires a messy amount of algebra. (The use of integral tables or Maple makes solving the integral easy.) This example is usually analyzed using this separation of variables method for students in Calculus and Differential Equation books.

Bernoulli's Method

However, there is a simpler method for solving this problem developed by Jakob Bernoulli in the late 1600's. This is simply a substitution technique that reduces the problem to a linear problem. Consider the logistic growth model with the substitution

If we differentiate this substitution, then the chain rule gives

Multiply the logistic growth model by - P ^-2. The resulting equation is 

or

This is converted into our variable z(t), and gives the differential equation 

or

If we make another substitution, say w(t) = z(t) - 1/M, then the problem above reduces to the simple form of the Malthusian growth model, which is very easily solved. Note that z(0) = 1/P₀, so w(0) = 1/P₀ - 1/M. Thus, we are solving the initial value problem

This has the solution

so

However, P(t) = z ^-1(t), so with a little algebra, we can write the solution of the logistic growth model as

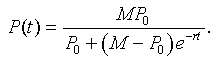
This analytical form provides a nonlinear equation that can be readily fit to the data.

References

[1] G. F. Gause, Struggle for Existence, Hafner, New York, 1934.

[2] G. F. Gause (1932), Experimental studies on the struggle for existence. I. Mixed populations of two species of yeast, J. Exp. Biol. 9, p. 389.