1. Monoculture Experiments with Two Yeast Populations
2. Logistic Growth Model
3. Qualitative Analysis of the Logistic Growth Model
   1. Equilibria
   2. Linearization
   3. Phase Portrait
4. Fitting the Logistic Growth Model - Yeast 
5. References

The last section introduced a series of experiments by Gause from the 1930s on populations of yeast competing for a limited source of nutrients. That section introduced the most basic of population models, the Malthusian growth models. However, the Malthusian growth model is limited in its scope for handling population growth and fails when populations become sufficiently large to interact with their environment in a significant manner. This section begins with a quick review of the Gause yeast experiments, where only a monoculture of the yeast is followed. We use these experiments to study the more complicated mathematical model for population growth, the logistic growth model. This model is fit to the data, then a discussion of the qualitative behavior of the model is presented.

Monoculture Experiments with Two Yeast Populations

We begin this section by reviewing the monoculture experiments by G. F. Gause [1] that were described in the previous section. His experiments examined the standard brewers yeast, Saccharomyces cerevisiae, and a slower growing yeast, Schizosaccharomyces kephir, in a closed environment with a fairly constant supply of nutrient. Clearly, the Malthusian growth models from the previous section would rapidly have the populations of yeast outstripping the food supply, so a better model is needed.

In this section, we examine only the two Gause experiments with the monocultures of yeast. The first table combines two experiments of Gause using only S. cerevisiae in the culture. As noted in the previous section, these data are shifted by 6 hours from the original experiment because no data were collected until 6 hours from innoculation of the yeast culture. The innoculation is said to be a single drop from a culture that had been growing for 72 hours and assumed to be at carrying capacity. Gause measured the volume of the yeast in a centrifuge tube with markings that were not specified to their exact volume. The volume of yeast gives a better understanding of the growth potential of these organisms instead of the actual population of the yeast.

Table for Single Species Culture of Saccharomyces cerevisiae

The second table combines the two experiments of Gause using only S. kephir in the culture. To match with the data for the experiment with S. cerevisiae, these data are also shifted by 6 hours from the original (which had the first measurement at 15 hours after innoculation). These data are collected over a much longer time period because of the slow growing nature of S. kephir.

Table for Single Species Culture of Schizosaccharomyces kephir

Below we show the graphs of the two monocultures. It is easy to see the early exponential rise of the population followed by a leveling off of the two monocultures. Clearly, these two species have significantly different growth rates and carrying capacities though they are grown under identical experimental conditions.

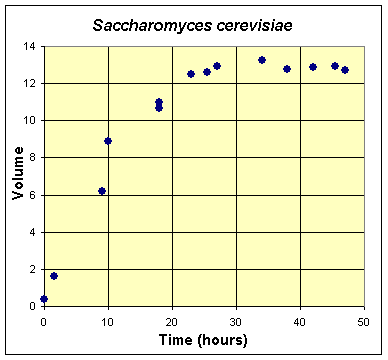
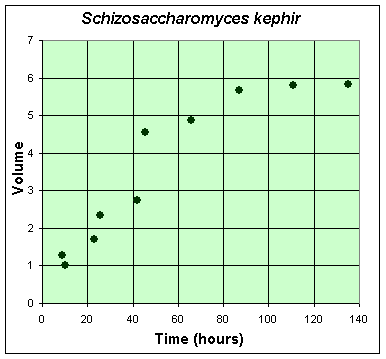
In the previous section we saw that the Malthusian growth could only fit the first few data points, so is an inadequate mathematical model to describe the dynamics of these experiments.

How do we improve on the Malthusian Growth model to fit these data?

Logistic Growth Model

For the most part, yeast are continually growing organisms, which implies that using differential equation models are the most appropriate. For an individual species with a population at time t given by P(t), we can write a general model using a differential equation of the form

P '(t) = f(t, P(t)),

for a general function f(t, P), representing the growth rate of the population. (Of course, this is the way that we can write any first order differential equation.) The Malthusian growth model has the form

P '(t) = rP(t).

This equation is classified as a linear constant coefficient differential equation, which given the initial condition P(0) = P₀, has the unique solution

The general differential equation above does not have a solution, so we need to determine what simplifications make sense for the experiments described above.

The Gause yeast experiments are closed systems with a careful design that ideally allows reproducibility. The experimental design with a continuous flow of nutrients and constant environmental conditions indicates the growth rate (reflected in the function f(t, P)) should only depend on the population variable P and not the time t. This implies that our growth model should be an autonomous differential equation of the form

P ' = f(P).

Note that the Malthusian growth model is autonomous and linear.

Consider a Maclaurin series expansion of the function f(P). If we write the first few terms of the series expansion, then

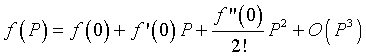
where O(P³) means order of P³. Since the system is closed, when the population is zero, then the population stays at zero (no growth), so

f(0) = 0.

The linear term comes from the Malthusian growth, so

f '(0) = r.

From the data, we know that the population growth rate declines for larger population. In biology, this is known as intraspecies competition. Mathematically, this implies that the next most significant term in the Maclaurin series expansion after the linear growth term must be negative. For reasons that will soon become apparent, we define

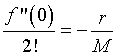
If the higher order terms can be ignored, then we have the differential equation given by

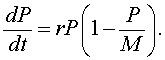
This is the logistic growth model.

The development above uses basic mathematical principles, but one can readily argue a similar term from an ecological perspective. In an environment with limited resources, then interactions between individuals results in fighting for those resources. The interaction between two individuals is modeled by the random contact, which is proportional to the product of their density (P²). This interaction is detrimental (or negative) because of the limited resources, so is given by a term of the form -rP²/M, which is the same as listed above from the Maclaurin series approach.

Qualitative Analysis of the Logistic Growth Model

The logistic growth model is a nonlinear differential equation. Most nonlinear differential equations cannot be solved, so we introduce you to the techniques of qualitative analysis of differential equations. However, since the logistic growth equation is solvable, we will also show how to solve this particular equation.

Equilibria

The first step in any qualitative analysis of a differential equation is to find all equilibria (if they exist). Equilibria are found by setting the right hand side of the differential equation equal to zero. Thus,

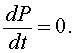
This means that there is no change in the growth of the population or the population is at equilibrium. In closed population models, one equilibrium is always the zero or trivial equilibrium. If we consider the logistic growth model, then the equilibria, P_e, satisfy

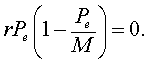
It is easily seen that

P_e = 0 or M.

The value M is the carrying capacity of the logistic growth model. The Gause experiments do provide good data for the carrying capacity of the yeast. An estimate of the carrying capacity is readily found by averaging the data points after growth of the yeast has leveled off. We can see that the growth has leveled off after about 24 hours, so if we average these data points, we obtain

Thus, the carrying capacity is about 12.9, which matches well with the value of 13.0 reported by Gause.

Linearization

The next step in qualitative analysis is to look at the behavior of the solution near the equilibria. This requires looking at the linearization of the differential equation near the equilibria. We begin with the linearization of the Logistic growth model at P_e = 0. It is easy to see that the linearization of this model is simply the Malthusian growth model or

P '(t) = rP(t).

As we have seen, this model grows away from P_e = 0, which gives this equilibrium as being unstable. (Its eigenvalue is r > 0.)

Next we linearize about P_e = M. We perform a Taylor series expansion about this equilibrium.

f(P) = f(M) + f '(M)(P - M) + O((P - M)²)

Because of the equilibrium, f(M) = 0. Since f '(P) = r - 2rP/M, it follows that

f '(M) = - r,

which implies that locally (near P_e = M) the solutions of the Logistic growth model exponentially approach the equilibrium. Thus, the equilibrium P_e = M is stable (with an eigenvalue - r < 0). This information suggests that all solutions for the monoculture of S. cerevisiae approach the carrying capacity near 12.9.

Phase Portrait

The computations from the previous section on Malthusian growth of S. cerevisiae in the Gause experiments gave an estimated initial volume and growth rate of about

P₀ = 0.7 and r = 0.25,

while the computation above gave the carrying capacity of

M = 12.9.

Since r/M = 0.0194, an reasonable approximation for the logistic growth model is given by the following initial value problem

P ' = f(P) = 0.25P - 0.0194P², with P(0) = 0.7.

The graph of f(P) gives more information about the behavior of the logistic growth model. As noted above, the equilibria occur at P_e = 0 and P_e = 12.9. Notice that to the left of P_e = 0, f(P) < 0, while to the right of P_e = 0, f(P) > 0. (The slope of the tangent line at P_e = 0 is the eigenvalue, r.) Thus, when P < 0, dP/dt < 0 and P is decreasing. (Note that this region is outside the region of biological significance.) When 0 < P < 12.9, then dP/dt > 0 and P is increasing. Furthermore, we can see that the greatest increase in the growth of the population occurs at P = 6.45, where the vertex of the parabola occurs.When P > 12.9, then again dP/dt < 0 and P is decreasing. (The slope of the tangent line at P_e = 12.9 is the eigenvalue, - r.)

This information allows us to draw what is called a Phase Portrait of the behavior of this differential equation along the P-axis. The behavior of the differential equation is denoted by arrows along the P-axis, which are easily directed by whether the function f(P) is positive or negative. This is diagrammed below using the graph of f(P). The open circle on the P-axis represents the unstable equilibrium, while the full circle on the P-axis represents the stable equilibrium.

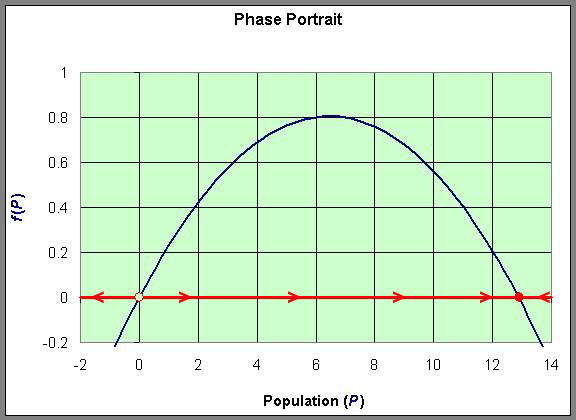
We can easily sketch the behavior of the solutions as functions of time using this phase portrait. Below is a graph of the solutions P(t) with t being the independent variable. The equilibria give rise to horizontal lines (meaning that P(t) does not change with time). When the initial values of P have the phase portrait pointing to the left, then the solution is decreasing, while arrows to the right on the phase portrait have the solutions increasing. The solutions are not allowed to cross paths in the time-varying diagram shown below (uniqueness of the solutions of the differential equation).

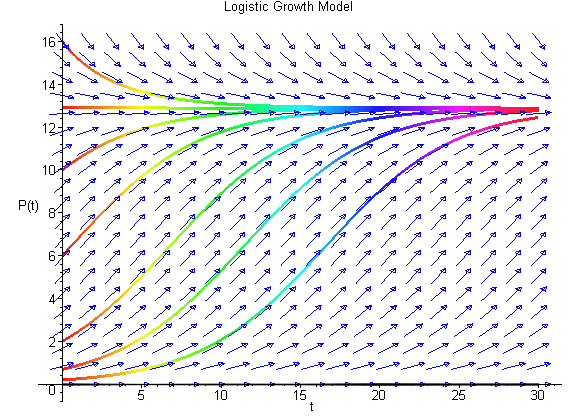
The solutions above show that all positive initial conditions result in solutions eventually tending towards the equilibirum at 12.9. Note that the third curve from the bottom solves the initial value problem listed above. The slope of the solution at any time can be seen in the figure above with the slope matching the value of f(P). The Maple commands to generate the figure above are given by

> with(DEtools):

> de := diff(P(t),t) = 0.25*P(t) - 0.0194*P(t)^2;

> DEplot(de, P(t), t=0..30, [[P(0)=0], [P(0)=0.2], [P(0)=0.7], [P(0)=2], [P(0)=6], [P(0)=10], [P(0)=16], [P(0)=12.9]],stepsize=.2, title=`Logistic Growth Model`,color=[.3*y(t)*(x(t)-1),x(t)*(1-y(t)),.1], linecolor=t/2,arrows=MEDIUM,color=blue,method=rkf45);

These experiments illustrate a problem when the experimentation does not use the feedback (shown in the introduction to the lectures). The experiments are meant to verify the logistic growth model, yet they were not redesigned after testing against the mathematical model. These experiments lack the very important initial values, which we will see are very important, and there are a paucity of data through the primary growth phase of the yeast. This leads to large margins of error in the choice of some of the parameters.

There is a special hyperlink to a section showing the solution of the logistic growth model. The section below examines how we find the growth parameters for these experiments.

Fitting the Logistic Growth Model - Yeast 

The best technique to fit the experimental data uses a nonlinear least squares method. This section will show how we can fit the data using either an Excel spreadsheet with Solver or MatLab's fminsearch routine.

A nonlinear least squares methods need some reasonable initial estimate before they are likely to converge. From our nonlinear least squares analysis of the Malthusian growth model and the estimate above of the carrying capacity, we obtain a reasonable initial guess using

P₀ = 0.7, r = 0.25, and M = 12.9.

The solution to the logistic growth equation is given by the formula

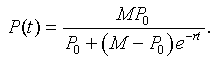
After a little algebra with the parameters listed above, our initial approximation to the logistic growth model is given by

The model reported by Gause [2] is

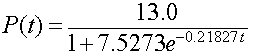
Below we will show this model, Gause's reported model, and the least squares best fit model that is presented in the next subsection.

Least Squares Fit to the Yeast Data

The computations above provide a reasonable fit to the data, but the initial condition will turn out to have too low a value, shifting the curve the the right of the best fit model. As we did when fitting the first four points to the Malthusian growth model, we want to apply a nonlinear least squares best fit to the data found at the beginning of this section. We will illustrate two computer methods for finding this best fit to the data, Excel's Solver routine and MatLab's fminsearch routine.

An Excel spreadsheet can be downloaded to view how to use Excel's Solver routine to best fit the logistic growth model to the data in the table at the beginning of this section. The method of finding this "best" model to fit the data is computed by minimizing the expression given by the formula

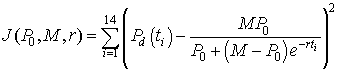
There are 14 data points with the volume of yeast at the different times (t_i) are denoted P_d(t_i). The model depends on the three parameters P₀, M, and r. The model volume of yeast given by the solution of the logistic growth equation with the three values inserted (starting with the values given above, P₀ = 0.7, M = 12.9, r = 0.25) at each of the times for the data points is subtracted from the value of the data at these times. This gives the error between the model and the data for a given set of parameters. Each of these error values is squared, and the sum of the squared errors is computed. Next Excel's Solver routine that can be found under the Tools heading is using to minimize this sum of squares error. (If the reader downloads the Excel spreadsheet, then the parameter values are found in the cells H2-H4 and the sum of square errors is in cell E17. The data are in columns B and C, while the model simulations are found in columns I-P.) The least squares best fit to the data, which is found by Excel gives the parameter values

which gives the best fit model to the yeast data as

This minimization process is very computationally intensive! Note that this model differs from the model presented by Gause in the literature. Most likely, Gause fixed the values of P₀ and M, then only minimized r, which can be done with a simple Newton's method. Recall that he did not have powerful computers in the early 1930s, so this was his most reasonable approach to finding a best fit model.

Next we present how you would approach this problem in MatLab. A major advantage of using MatLab is that MatLab's fminsearch routine has information on the numerical method that is being employed and gives you access to the code. This is especially important when the minimization fails (allowing improved numerical techniques to be employed).

In MatLab, we first create the logistic growth function as a function of time, t, and with the vector of parameters, p = [P₀, r, M]. Our function is called logrow and is given by:

function pop = logrow(t,p)
pop = p(3)*p(1)/(p(1)+(p(3)-p(1))*exp(-p(2)*t));

Next we need the nonlinear sum of square error functional J(p) that will be used to minimize the logistic growth model parameters p to fit the data in the table above. (Time data is tdata, and population/volume data is pdata.) Our function is called leastgrow and is given by:

function J = leastgrow(p,tdata,pdata)
n = length(tdata);
Jtemp = 0;
for i=1:n,
Jtemp = Jtemp + (pdata(i)-logrow(tdata(i),p))^2;
end
J = Jtemp;

Finally, we call on the fminsearch routine in MatLab to find the minimum vector p. We create vectors td from the time data and pd from the population/volume data. The command in MatLab to execute our program is given by

>> [p,fval,exitflag] = fminsearch(@leastgrow,[0.7 0.25 12.9],[],td,pd)

The resulting values agree with the ones listed above by Excel.

Below we graph the solutions presented above

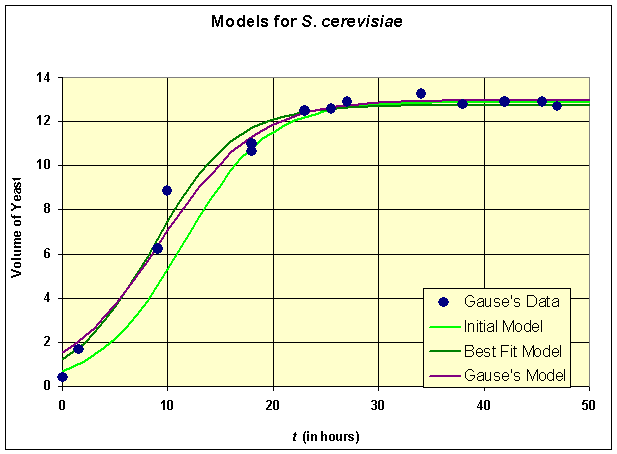
All three models provide reasonable estimates to the data though our initial model appears to be shifted a little to the right of the data. The carrying capacities of all three models are very close, which is what we would expect from the qualitative behavior analysis. There is a fair discrepancy in the growth rates, which is largely due to the fact that there needed to be more data points acquired in the experiments during the primary growth period. This is where experimenters and modelers need to develop better communication links to improve both the models and the experimental design. Review the original cartoon introducing this course of how experiments and models can be refined.

References

[1] G. F. Gause, Struggle for Existence, Hafner, New York, 1934.

[2] G. F. Gause (1932), Experimental studies on the struggle for existence. I. Mixed populations of two species of yeast, J. Exp. Biol. 9, p. 389.