1. Chemostat with Two Yeast Populations
2. Malthusian Growth Model
   1. Discrete Malthusian Growth Model
   2. Solution of the Discrete Malthusian Growth Model
   3. Fitting the Discrete Malthusian Growth Model
   4. Continuous Malthusian
   5. Solution of the Continuous Malthusian Growth Model
   6. Fitting the Continuous Malthusian Growth Model
3. References

This course begins with a study of yeast competing for a limited source of nutrient. (Population models are covered in the second section of the text.) This section starts with a description of the Gause yeast experiments. Based on the experiments, several mathematical models are discusssed with the techniques required to study them. The models are fit to the data, then a discussion of the qualitative behavior of the models is presented.

Chemostat with Two Yeast Populations

One method for maintaining a culture of yeast used in brewing beer is to create a chemostat. A chemostat is a large vat, where nutrients are pumped into the vat with a constant flow rate, then the growing culture is removed at the same flow rate. Under ideal conditions, a monoculture of yeast grows exponentially at first, then as the population becomes sufficiently large, the concentration of yeast levels off. At a certain level, known as the carrying capacity, the population of yeast balances the supply of nutrient entering the vat. At this stage, the the population (or concentration) of yeast remains constant with as many yeast being born in each unit of time as are flushed out from the chemostat per unit time. These conditions guarantee a constant supply of uniform concentration of the yeast flowing from the chemostat. This allows the brewmaster a consistent supply of the yeast culture, which ensures a uniform product with the desired characteristics. Unfortunately, it is almost impossible to keep a consistent monoculture of the yeast. The vat often gets infected with a competing yeast or bacteria that destroys the uniformity and lowers the quality of the beer. Below is a cartoon illustrating the idea of a yeast culture growing in a chemostat.

Ideally, we would like to develop a mathematical model for the chemostat described above, especially when a contaminating species invades the culture. We begin with an analysis of some classical studies from the 1930s that carefully examine cultures of yeast that have a fixed supply of nutrient. In the book Struggle for Existence, G. F. Gause [1] describes his experiments, which do not use an actual chemostat, but rather changed the nutrient in a closed vessel regularly (every 3 hours). This is roughly equivalent to a chemostat. He performed a number of experiments to test competition of microbial species. One set of experiments examined the standard brewers yeast, Saccharomyces cerevisiae, and a slower growing yeast, Schizosaccharomyces kephir. He tested these organisms in monocultures to find their growth parameters with his experimental set up, then he mixed the cultures to determine how the organisms reacted when they competed in the same nutrient medium. He notes that though he used a standard medium, he was not certain of all the concentrations of the different components in the medium, which complicates the ecological model since the species could be utilizing different components of the medium.

Below we present a series of tables showing the two yeast species competing in the Gause experiments. The first table combines two experiments of Gause using only S. cerevisiae in the culture. These data are shifted by 6 hours from the original experiment because no data were collected until 6 hours from innoculation of the yeast culture. The innoculation is said to be a single drop from a culture that had been growing for 72 hours and assumed to be at carrying capacity. Notice that Gause measured the volume of the yeast rather than the population, which is probably a better measure of the organism's ability to absorb the nutrients. The volume quoted in the papers only indicated units marked on a centrifuge tube after spinning the culture down, so absolute units are not available.

Time (hr)	0	1.5	9	10	18	18	23	25.5	27	34	38	42	45.5	47
Volume	0.37	1.63	6.2	8.87	10.66	10.97	12.5	12.6	12.9	13.27	12.77	12.87	12.9	12.7

The second table combines two experiments of Gause using only S. kephir in the culture. To match with the data for the experiment with S. cerevisiae, these data are also shifted by 6 hours from the original (which had the first measurement at 15 hours after innoculation). These data are collected over a much longer time period because of the slow growing nature of S. kephir.

Time (hr)	9	10	23	25.5	42	45.5	66	87	111	135
Volume	1.27	1.0	1.7	2.33	2.73	4.56	4.87	5.67	5.8	5.83

Finally, we present a table that shows the competition of S. cerevisiae and the slower growing S. kephir that Gause performed in two experiments. Once again the data are shifted by 6 hours from the original experiment to match the first time when data was actually collected after innoculation of the yeast cultures.

Time (hr)	0	1.5	9	10	18	18	23	25.5	27	38	42	45.5	47
Volume (S. cerevisiae)	0.375	0.92	3.08	3.99	4.69	5.78	6.15	9.91	9.47	10.57	7.27	9.88	8.3
Volume (S. kephir)	0.29	0.37	0.63	0.98	1.47	1.22	1.46	1.11	1.225	1.1	1.71	0.96	1.84

We are now presented with a collection of raw data and would like to explain these data with a mathematical model for the growth of yeast.

How do we create a mathematical model from these data?

We should probably begin this study by finding and analyzing the simplest of population models.

Brewer's yeast, S. cerevisiae, is a simple eukaryotic organism (cells with nuclei) that reproduces asexually by a process of budding. Given an unlimited supply of nutrients (which is the case for lower densities of the yeast), then during any fixed period of time, there is a certain probability that any particular yeast will produce a new bud that will eventually grow to become a mature yeast. There is also a certain probability that a grown yeast will die. From the data on the time, a natural unit of time might be 1/2 hour (though one could argue for minutes or hours equally well). Under conditions where the yeast populations are low relative to the supply of nutrients, then the rate of budding and death should be fairly constant.

Let Dt = 1/2 hour be our unit of time. Let b be the budding rate per unit volume of yeast (recall that our yeast data above are in volume of cells measured in a centrifuge tube) per unit time Dt. This budding rate will again be in volume units of yeast. Let d be the death rate per unit volume of yeast per unit time Dt. Then the total rate of increase in volume of yeast per unit time, Dt, per unit volume of yeast (or decrease should the death rate exceed the rate of budding) is given by

Let P(t) be the volume of yeast at time t, then from our discussion above, when the population of the yeast is low relative to the concentration of nutrients, it follows that on average

This says that the difference between the populations of yeast at t and t + Dt is the rate of growth of the yeast volume times the amount of yeast present in the culture. This equation is readily rearranged into the equation

Let the integer n represent the number of half hour intervals after the initial collection of data at t = 0 and define P_n to be the population for the n^th half hour after t = 0 (with P₀ representing the volume of yeast at t = 0 ). The equation above can be written

where n is the number of half hour periods after the initial collection of data.

This equation is the Discrete Malthusian Growth model (named after the work of Thomas Malthus (1766-1834)). The Discrete Malthusian Growth model is a special example of Discrete Dynamical systems or Difference equations, which provide the best modeling setting for describing deterministic systems that are given only at discrete times. We will probably study more of these models as the semester progresses (or at least use this discrete set up as the staging ground to develop the more easily handled continuous models). Population models using difference equations are commonly used in Ecological modeling as one can often determine the population of a species or collection of species knowing the population of the previous generation of the species being studied. The Malthusian growth model states that the population of the next generation is simply proportional to the population in the current generation, which is what is written in the equation above.

Solution of Discrete Malthusian Growth Model

There are not many discrete models that have an explicit solution. However, it is easy to solve the discrete Malthusian growth model. From the model above, we see that

Thus, the general solution of this model is given by

This shows why Malthusian growth is also known as exponential growth. The solution to the model that is given by the equation above is an exponential function with a base of 1+ r and power n representing the number of iterations after the initial population is given.

Fitting the Discrete Malthusian Growth Model to the Yeast Study

Recall that the assumptions on this model are that the yeast volume is relatively small compared to the amount of nutrient available. Thus, we predict that the Malthusian growth model will only approximate the early phases of the data. So how do we fit the early data?

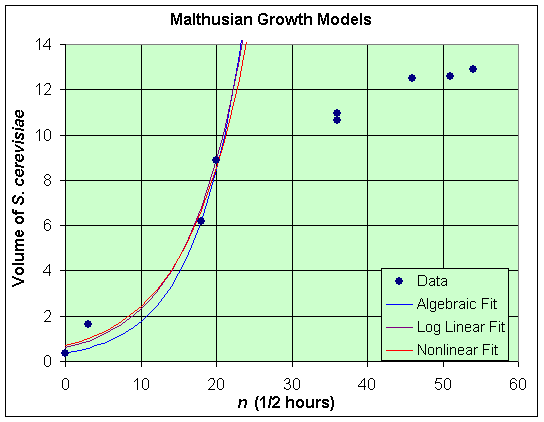
Based on the assumption for the discrete Malthusian growth model,  we can assume that this exponential growth will only be valid for populations below half the carrying capacity. In the data for S. cerevisiae, we see that the carrying capacity is approximately 13, so only the first 3 (or possibly 4) data points are in the range where we expect Malthusian growth.

What techniques can be employed to find the best fit to these data?

This question is one of the most important aspects of modeling, yet is not regularly studied in a mathematics curriculum. This is the inverse problem or parameter identification problem for dynamical systems. The experiments have several sources of error in measurement, including the amount of culture transferred initially. From the solution of the Malthusian growth model, we see that there are two unknown parameters to identify, P₀ and r. Below we list 3 techniques for finding these parameters.

1. Algebraic fit to the data
2. Exponential fit (Linear least squares best fit to logarithm of data)
3. Nonlinear least squares best fit

Each of these techniques has its strengths and weaknesses. After the discussion of each of these, we present a graph showing each of these techniques. An Excel worksheet is provided to show the second two methods described above.

Algebraic fit to the data

A quick and easy method for fitting the data to the Malthusian growth model is to examine the graph of the data, then choosing two of the most representative data points and finding the parameters P₀ and r that fit these two data points. For our data on S. cerevisiae, we choose the first and third data points, (n, P) = (0, 0.37) and (n, P) = (18, 6.2). (Note that because Dt = 1/2 hour, this third data point occurs at 9 hours with n = 18.) From the Malthusian growth model, the first data point states that

The third data point gives

It follows that

Thus, using these two data points, we have the Malthusian growth model

Exponential fit (Linear least squares best fit to logarithm of data)

Suppose we want to find the best fit through the first 4 data points from the data on S. cerevisiae. Notice that if we take the logarithm of the Malthusian growth model, then we have

By taking the logarithm of the volume of S. cerevisiae in the culture, then the equation above shows that we are trying to find the best straight line fit through the logarithm of the volume data, ln(P_n), and iteration, n. The slope of this best fit line, ln(1 + r), and intercept, ln(P₀), give the best Malthusian growth model. A basic course in Statistics shows how to find best straight lines through data. (This best fit can be found in Excel using its special Exponential fit under the Trendline feature with the Chart option.) The best straight line fit to the logarithm of the volume data is given by

It follows that

Thus, the best Malthusian growth model is given by

Nonlinear least squares best fit

The most direct method is to minimize the sum of the square error between the data and the Malthusian growth model. However, this is actually the most difficult calculation. It requires finding the minimum of a nonlinear function of two variables. For the data on S. cerevisiae, the least squares functional is given by

where

Solving this type of problem is common in Numerical Analysis courses. This nonlinear functional can be readily solved using Excel's Solver or MatLab's fminsearch function. (The former is shown on the hyperlinked Excel spreadsheet, and details on how Excel's Solver works are provided through this hyperlink. MatLab help can be used to find information on its nonlinear routine that is employed, the Nelder-Mead simplex (direct search) method. MatLab has an advantage in that its programming code is readily accessible.) In both of these cases, an initial guess is required to initiate the routine. Because this is a nonlinear problem, then the initial guess can have a significant effect on whether the solution converges. Recall the sensitivity on Newton's method from your earlier courses. (We will review Newton's method later in this course for those of you who have forgotten this very important mathematical technique.) The first method described above (the algebraic solution using two data points) gives a good initial guess.

The solution to this minimization problem give the parameters

Thus, the best Malthusian growth model is given by

A graph of each of these models is shown below with the first 30 hours of data. We see that the 3 methods given above give very similar qualitative behavior (typical exponential growth) with all models fitting the first 4 data points reasonably well, but failing after that as we would expect from both the techniques employed and from the discussion of the experiment. Notably, there is very little difference between the exponential fit to the data and the nonlinear least squares best fit.

 

The discrete Malthusian growth model given above had the form

P_n+1 = (1 + r)P_n,

where P_n is the volume of the yeast at time n (with this time being 1/2 hour units) and r is the rate of growth (per 1/2 hour). This equation can be rearranged to give

which says that the change in volume of the yeast between the (n + 1)^st time period and the n^th time period is proportional to the volume of the yeast at the n^th time period.

Now we want to write this model in terms of continuous time variables. Define P(t) to be the volume of the yeast at any time t. Assume that r is the rate of change of the volume of the yeast per unit time per unit volume of the yeast. If we let Dt be a small interval of time, then the change in volume of the yeast between t and t + Dt, satisfies the equation

Biologically, this equation says that the change (difference) in the volume of the yeast over a small period of time is found by taking the rate of growth times the volume of the yeast times the interval of time Dt. The equation above can be rearranged to give

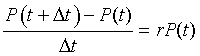
The right hand side of the equation readily transforms into a derivative as we take the limit of Dt tending toward zero. Thus, in the limit this model reduces to the differential equation

This is the continuous Malthusian growth model.

Solution to the Malthusian Growth Model

The differential equation describing the continuous Malthusian growth model says that the derivative of an unknown Population function P(t) is equal to a constant times the unknown Population function. (The rate of change of a population is proportional to the population.) The only function that we know that is a derivative of itself is the exponential function. We try a solution of the form

where c is an arbitrary constant. But P '(t) is cre^rt, which is rP(t), so satisfies the differential equation. If we add an initial condition P(0) = P₀, then the unique solution becomes

This is another reason why Malthusian growth is often called exponential growth. This solution is equivalent to the solution of the discrete Malthusian growth model with the exception that the time is in units of hours, which corresponding affects the growth rate ^r.

Fitting the Continuous Malthusian Growth Model

The fitting of this model is equivalent to the fitting of the discrete Malthusian growth model with the only change being the units of time and the formula that is used. If we repeat the curve fits above, then we obtain the following continuous Malthusian growth models.

Algebraic fit to the data

We use the first and third data points for S. cerevisiae, (t, P) = (0, 0.37) and (t, P) = (9, 6.2) to fit the continuous Malthusian growth model and find the parameters P₀ and r. From the model, the first data point gives

The third data point gives

It follows that

so the continuous Malthusian growth model satisfies

Exponential fit (Linear least squares best fit to logarithm of data)

Again we take the first 4 data points from the data on S. cerevisiae, then fit the best straight line through the logarithm of the data. The best straight line fit to the logarithm of the volume data is given by

It follows that

Thus, the best continuous Malthusian growth model is given by

Nonlinear least squares best fit

Finally, we again minimize the sum of the square error between the data and the continuous Malthusian growth model. For the first data points on S. cerevisiae, the least squares functional is given by

where

The solution to this minimization problem give the parameters

Thus, the best Malthusian growth model for this nonlinear least squares fit is given by

These solutions are completely equivalent to the discrete cases above. Another Excel worksheet is provided by a hyperlink to see the computations. A graph of these models with the data would match the graph above for the discrete Malthusian growth model, except that scale on the horizontal axis would have a factor of 1/2.

References

[1] G. F. Gause, Struggle for Existence, Hafner, New York, 1934.

[2] G. F. Gause (1932), Experimental studies on the struggle for existence. I. Mixed populations of two species of yeast, J. Exp. Biol. 9, p. 389.