|
|
Math 122 - Calculus for Biology II |
|
|---|---|---|
|
|
San Diego State University -- This page last updated 09-Apr-03 |
|
|
|
Math 122 - Calculus for Biology II |
|
|---|---|---|
|
|
San Diego State University -- This page last updated 09-Apr-03 |
|
This section introduces a new integration technique, integration by substitution. When an integral is not easily recognizable as one of the basic forms seen in earlier sections, then we first attempt to find a substitution that reduces the integral to a simpler form, allowing integration. This technique is applied to solving the logistic growth model and a differential equation describing the motion of an object subject to gravity.
Logistic Growth Model for Yeast
One of the principle models discussed in biological literature is the Model of Logistic Growth. Most organisms when grown in an environment with a constant amount of food will begin after a lag period to grow according to Malthusian growth, as we studied at the beginning of this section on differential equations. However, as the food source becomes limiting or waste products create a toxic environment, the growth of the organism slows and the population levels off or even starts to decline. This behavior is modeled by adding a negative quadratic term to the Malthusian growth model, giving the logistic growth model, which has the following form:
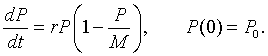
G. F. Gause [1] in his book Struggle for Existence created a series of experiments to study this phenomenon and other issues of competition between microbial organisms. We will examine the combined results from two of his experiments performed on standard brewers yeast, Saccharomyces cerevisiae. His experiments took a culture of S. cerevisiae and placed them in a closed vessel, where the nutrient was changed regularly (every 3 hours). This simulates the condition of the equation above where there is a constant source of nutrient. He measured the volume of these organisms (rather than direct population counts) to find the growth parameters for the logistic growth model given above.
Below we present a table of his results and give the best logistic growth model from the data. These data are shifted by 6 hours from the original experiment because no data were collected until 6 hours after innoculation of the yeast culture.
Table for Single Species Culture of Saccharomyces cerevisiae
|
Time (hr) |
0
|
1.5
|
9
|
10
|
18
|
18
|
23
|
25.5
|
27
|
34
|
38
|
42
|
45.5
|
47
|
|
Volume |
0.37
|
1.63
|
6.2
|
8.87
|
10.66
|
10.97
|
12.5
|
12.6
|
12.9
|
13.27
|
12.77
|
12.87
|
12.9
|
12.7
|
If we let P(t) be the population for S. cerevisiae, then the differential equation for this yeast population that best fits these data is given by
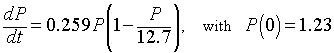
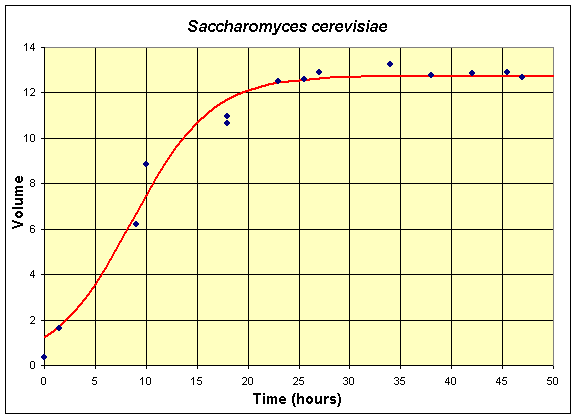
The graph below shows the Gause experimental data and the solution to the logistic growth model that best fits these data.
How do we find the solution to this nonlinear differential equation? This is clearly a separable equation, but the integral for P is not one of the easily recognizable forms. The solution of the integral for P actually involves two integration techniques, but we'll concentrate on the the integration by substitution.
Integration is an operation that is the inverse of differentiation. Though we can usually find the derivative of any differentiable function, there are many functions that do not have an antiderivative. However, we would like to extend our integration techniques beyond the basic integrals learned earlier. Integration by substitution provides another means of evaluating integrals. This technique is the inverse of the chain rule of differentiation. The idea behind the substitution technique is to find a function that reduces an integral to one of the basic integrals already solved.
Examples: Below we demonstrate the substitution technique through example.
1. In the first example we consider the function (x + a)n, where a is constant. The substitution that we make is u = x + a. The derivative of this gives du = dx. Thus, we see that
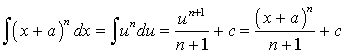
2. Our next example uses the substitution u = -x2, so du = -2x dx.
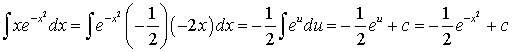
3. In this example, let u = x2 + 2x + 4, so du = (2x + 2)dx.
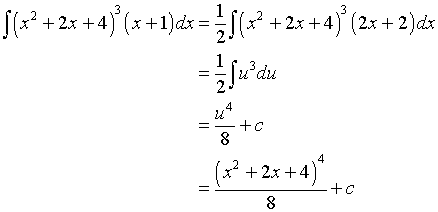
Note that in all of the examples above we chose u such that when u and du are substituted for the expression of x under the integrand, the remaining integral became of one of the basic integrals we have solved earlier. The hard part of this technique is recognizing what makes a good substitution.
There are a few choices that are very natural for a substitution. We have demonstrated in the examples above a couple of the natural substitutions are:
1. Let u be any expression of x in the exponent of the exponential function e or the argument of any trigonometric functions or the logarithm function. (See Example 2.)
2. Let u be an expression of x inside parentheses raised to a power, where you should be able to see the derivative of that expression multiplying this expression to a power. (See Examples 1 and 3.)
Return to the Logistic Growth Model
The general model for Logistic Growth is given by the differential equation
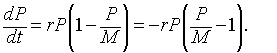
We apply the separation of variables technique to this differential equation and obtain the following integrals to solve:
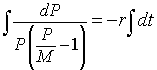
The integral on the right is very easy to solve, but the one on the left is more complicated. An advanced technique from algebra allows the fraction in the integral above to be split into two simple fractions. Algebraically, it can be easily shown that
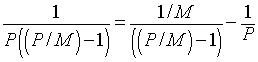
It follows that the left integral above can be written
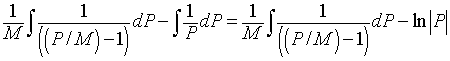
To evaluate the other integral, we make the substitution
u = P/M - 1, so du = dP/M.
Thus,
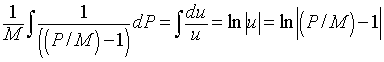
With this information, the implicit solution to the logistic growth equation is
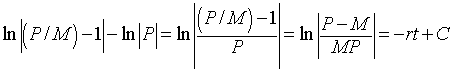
By exponentiating this result, we find
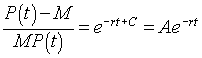
Solving this for P(t) gives
![]()
With the initial condition P(0) = P0 and some algebra, the general solution to the logistic equation is given by
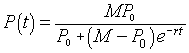
For the Gause yeast experiments, the best fit model shown in the graph above is given by the expression
![]()
This function creates the standard S-shaped curve of logistic growth and has the carrying capacity of 12.7.
There is an alternate way to solve the logistic growth equation using Bernoulli's method of substitution. Most students find this alternate method simpler to understand.

A classic problem from physics is the study of an object shot away from a planet that is acted upon by only gravitational forces. We would like to study the velocity of this object as it moves away from the surface of a planet using Newton's law of gravitational attraction, but ignoring any air resistence. Newton's law of gravitational attraction states that the force of attraction is inversely proportional to the square of the distance between the masses. The fundamental law to study the velocity of this object is Newton's law of motion, which states that the mass of the object times the acceleration is equal to the sum of all the forces acting on the object.
Suppose that an object of mass m is projected upward from Earth's surface with an initial velocity V0. If x is the distance from the surface of the Earth, then ignoring air resistence, but accounting for the variation of the Earth's gravitional field, Newton's law of motion gives the acceleration of the object, a, as follows
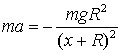
where g is the acceleration of gravity at the surface of the Earth and R is the radius of the Earth.
We know that acceleration is the time derivative of the velocity or a = dv/dt. However, we want to know the velocity as a function of the distance rather than time. Note that the velocity v = dx/dt, where x is the distance from the Earth. We can apply the chain rule of differentiation to give
If we substitute this information into the expression given by Newton's law of motion, then the differential equation describing the velocity as a function of the distance from the surface of the Earth for the object is given by
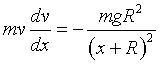
We would like to solve this differential equation and determine the smallest velocity required so that an object does not return to Earth.
In the equation above, the variables v and x are already separated. After dividing by m, the differential equation can be written in the integral form:
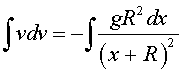
The left hand side is easy to integrate. However, the right hand side requires the technique of substitution. The integral on the right above for this problem of velocity in a gravitational field is very similar to our first Example in our discussion for substition techniques for integration. Let u = x + R, then du = dx. We see that
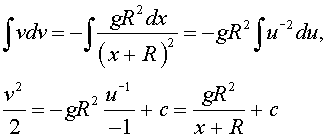
Thus, we can write the solution as either
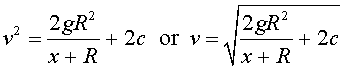
The initial condition gives v(0) = V0. This is substituted into the expressions above to give
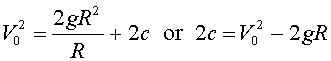
Therefore, the solution is given by
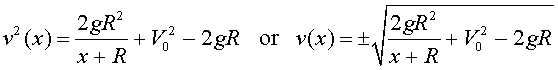
The escape velocity is the velocity at the surface of the planet, V0, required for an object to escape the gravitational pull of a planet and not return. In other words, the velocity v(x) never reaches zero as x increases. The smallest such velocity would be if v(x) reaches zero as x increases to infinity. As x goes to infinity, the expression 2gR2/(x+R) goes to zero. Thus, we find the escape velocity by solving
For Earth, g = 9.8m/sec2 and R = 6,378 km, so the necessary V0 for escape velocity is V0 = (2*0.0098*6378)1/2 = 11.2 km/sec.
[1] G. F. Gause, Struggle for Existence, Hafner, New York, 1934.