1. Logistic Growth Model
2.  
3. Problems

Logistic Growth Model

Earlier we saw that the discrete logistic growth model is an improvement over the discrete Malthusian growth model because of the additional term that accounts for crowding of the population. This model was shown to work quite well for a yeast population and in the Labs for different populations of beetles. One major problem with the discrete logistic growth model is that it has no explicit solution. Furthermore, there are examples of the discrete logistic growth model that become chaotic in behavior.

At the beginning of the our study of differential equations, we saw that by taking smaller time steps in the discrete Malthusian growth model, the limiting model becomes the continuous Malthusian growth model given by a simple differential equation P' = kP, with the solution P(t) = P₀e^-kt. The discrete logistic growth model is given by

which can be written

As in the arguments made for going from the discrete Malthusian growth model to the continuous Malthusian growth model, where the time interval between n and n+1 become small, the continuous logistic growth model follows from the equation above and can be written

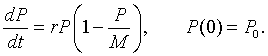
Can we solve this differential equation?

The continuous logistic growth model is clearly a separable differential equation, but separating variables leaves you with an integral that requires a technique of integration called partial fraction decomposition and then still requires a messy amount of algebra. (This is the usual way this problem is solved for students in Calculus books.) However, there is a simpler method for solving this problem developed by Jakob Bernoulli in the late 1600's. This is simply another substitution technique (which have been the topic of study in many of our previous sections).

Let us see what happens to the logistic growth model given above when we make the substitution

If we differentiate this substitution, then the chain rule gives

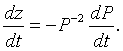
Let us multiply the logistic growth model by - P ^-2. The resulting equation is

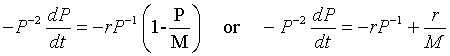
This is converted into our variable z(t), and gives the differential equation

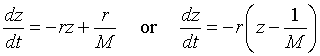
Notice that the last form of the differential equation in z(t) is basically the same problem that we encountered when solving the differential equations for Newton's law of cooling or pollution in a lake. Thus, we want another substitution, say w(t) = z(t) - 1/M. Note that z(0) = 1/P₀, so w(0) = 1/P₀ - 1/M. Thus, we are solving the initial value problem

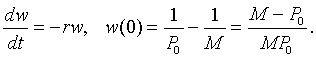
This has the solution

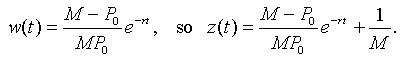
However, P(t) = z ^-1(t), so with a little algebra, we can write the solution of the logistic growth model as

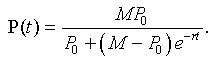
Example:

Problems: