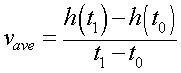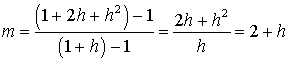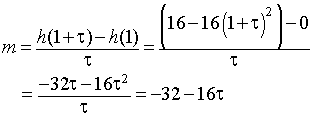Math 121 - Calculus for Biology I Spring Semester, 2009 Velocity and Tangent Lines
	© 1999, All Rights Reserved, SDSU & Joseph M. Mahaffy San Diego State University -- This page last updated 14-Mar-09

1. Cats and Gravity
2. Falling Ball Revisited
3. Flight of a Ball under Gravity
4. Tangent Line Interpretation
5. Worked Examples
6. Applet for Derivative as a Tangent Line
7. Velocity of the Cat
8. References

• An object falling under the influence of gravity is a classical study in differential Calculus

Cats and Gravity

 

• Cat have evolved to be one of the best mammalian predators
• Domestic cats have been shown to responsible for up to 60% of the deaths of songbirds in some communities
• They are adapted to hunting in trees
• Cats have a very flexible spine for hunting
• This flexibility allows them to rotate rapidly during a fall

• Humans have been fascinated by this ability of a cat to right itself
• Many scientific studies of cats falling
  • One study of cats falling out of New York apartments showed that paradoxically the cats falling from the highest apartments actually fared better than ones falling from an intermediate height
  • The cat remains tense early in the fall
  • With greater heights the falling cat relaxes and spreads its legs to form a parachute
  • This slows its velocity a little and results in a more even impact
  • From intermediate heights, the cat basically achieves terminal velocity, but the tension causes increased likelihood of severe or fatal injuries

• The early stages of the fall result from acceleration due to gravity
• Newton's law of motion says that mass times acceleration is equal to the sum of all the forces acting on an object
• Velocity is the derivative of position
• Acceleration is the derivative of velocity

• Suppose that a cat falls from a branch that is 16 feet high
• The height of the cat satisfies the equation

• How long does this cat fall and what is its velocity when it hits the ground?

• The first question is easily answered,

which occurs when t = 1

• However, the velocity at t = 1 requires more work
• We will show that the cat has a velocity, v(1) = -32 ft/sec (or about 21.8 mph)

• Below is an applet showing
  • The height of the ball as a function of time, h(t)
  • The average velocity of the ball as a function of time
• Recall that average velocity is the difference in positions divided by time

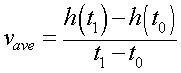
source for dropspeed4a
Alternate link

• The height of the ball as a function of time follows a parabolic path
• The distance of the ball between successive flashes increases with time
• The velocity becomes more negative and follows a straight line
• The derivative of a quadratic function will be a linear function

• Consider a ball thrown vertically under the influence of gravity, ignoring air resistance
• The ball begins at ground level (h(0) = 0 cm)
• It is thrown vertically with an initial velocity, v(0) = 1960 cm/sec
• The acceleration of gravity is g = 980 cm/sec²
• The height of the ball for any time t (0 < t < 4) is given by

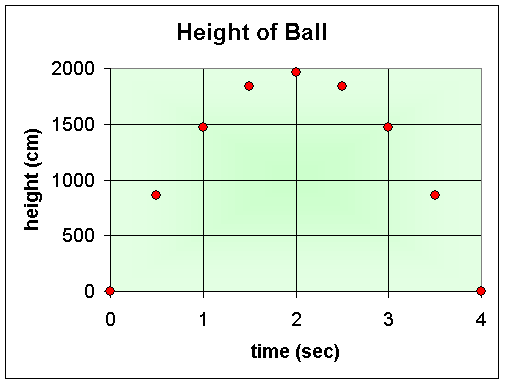
• The graph for the height of the ball h(t) over the first 4 seconds, showing the position of the ball at every 0.5 sec

 

• Compute the average velocity between each point on the graph
• The average velocity is the difference between the heights at two times divided by the length of the time period
• For convenience, associate the average velocity with the midpoint between each time interval considered

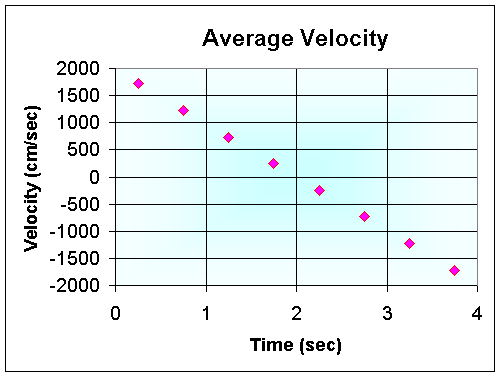
• A graph of the average velocities is below
• The graph of the average velocities is a straight line
• The average velocity is zero when the ball reaches its maximum height
• The velocity should be zero when the ball is at the top of its flight

 

• Consider the graph of the height with data every 0.1 sec

 

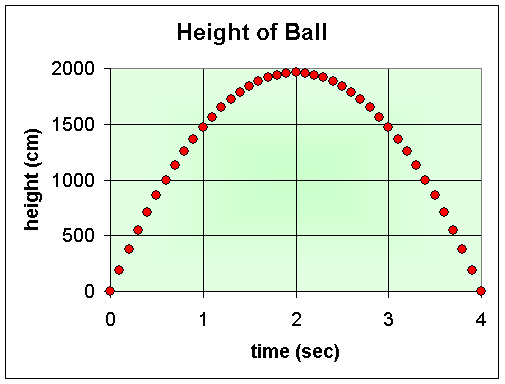
• How does this affect the average velocity computation?
  • The distance between successive heights is now closer
  • But then the intervening time interval is also closer together
• The average velocity between t₁ = 0.2 and t₂ = 0.3 has h(t₁) = 372.4 cm and h(t₂) = 543.9 cm, so v(0.25) = 1715 cm/sec, the same as before

 

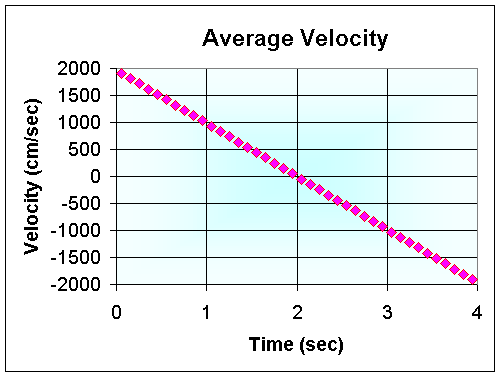
• The average velocity data lie on the same straight line as before

• This straight line function is the derivative of the quadratic height function h(t)
• The calculation suggests that the derivative function is independent of the length of the time interval chosen; however, this was specific to the quadratic nature of the height function
• We will learn in the coming sections how to take derivatives of more functions.

• The average velocity is the same calculation as the slope between the two data points of the height function
• The slope of the secant line between two points on a curve
• Geometrically, as the points on the curve get closer together, then the secant line approaches the tangent line
• The tangent line represents the best linear approximation to the curve near a given point
• Its slope is the derivative of the function at that point

Example: Consider the function

• Find the equation of the tangent line at the point (1,1) on the graph
• A secant line is found by taking two points on the curve and finding the equation of the line through those points
• The animated gif below shows a sequence of secant lines that converge to the tangent line by taking the two points closer and closer together

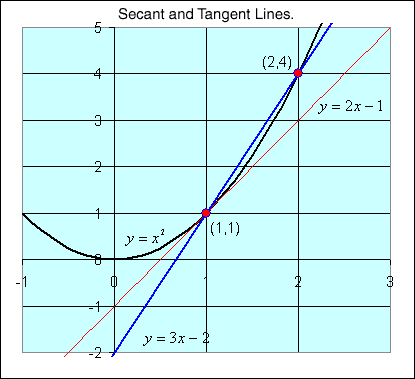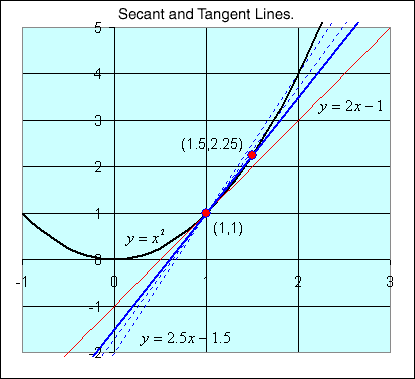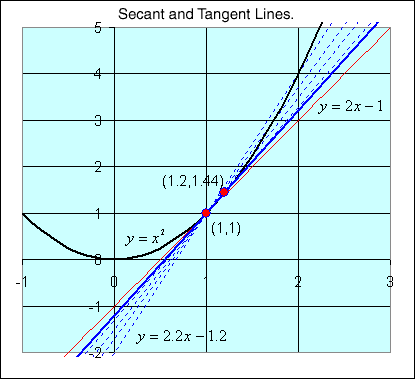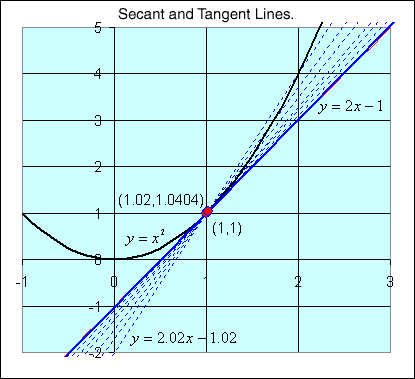
• Consider the secant line through the points (1,1) and (2,4)
• This line has a slope of m = 3, and its equation is

• Next consider the pair of points on the curve y = x², (1,1) and (1.5, 2.25)
• This line has a slope of m = 2.5, and its equation is

• The secant line through the points (1,1) and (1.1, 1.21) has a slope of m = 2.1
• Its equation is

• Consider the x value x = 1+ h for some small h
• The corresponding y value y = (1+ h)² = 1 + 2h + h²
• The slope of the secant line through this point and the point (1,1) is

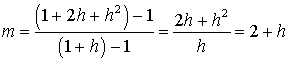
• The formula for this secant line is

• As h gets very small, the secant line gets very close to the tangent line
• Its not hard to see that the tangent line for y = x² at (1,1) is

• The slope of the tangent line, m = 2, is the value of the derivative of y = x² at x = 1.

• Worked Examples

• The tangent line can be found by taking a sequence of secant lines with the x values getting closer together
• These calculations are clearly very tedious
• The geometric view of the tangent line is very easy to visualize
• Our applications relate the derivative to growth rate and velocity and are simply the slope of the tangent line
• Below is an applet for exploring the derivative of a cubic function (left)
• Its derivative is on the right
• Click on the figure on the left and a point with the tangent line will appear on the graph
• The value of the slope of the tangent line appears in the graph on the right

source for slope3c
Alternate link

Several points of particular interest

• The graph on the left is a cubic function, while the graph of its derivative is a quadratic
• As you approach a maximum (or minimum) for the cubic function, the value of the derivative goes to zero and the sign of the derivative function changes
• This is an important application of the derivative

Velocity of the Cat

•  Our example of a cat falling from a branch that is 16 feet high satisfies the equation

• The cat hits the ground ofter only one second of falling
• To find the velocity of the cat, we need to determine its the slope of the tangent line for h(t) near t = 1.

• Find the height for a small increment of time after t = 1, say t = 1 + t
• The slope of the secant line between the heights at t = 1 and t = 1 + t is

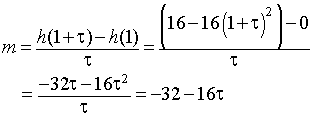
• The velocity at t = 1 is the slope of the tangent line
• Let t go to zero, then the velocity of the cat at t = 1 is

References:

[1] Jared M. Diamond (1988), Why cats have nine lives, Nature 332, pp 586-7.