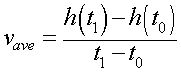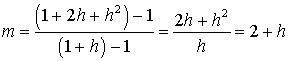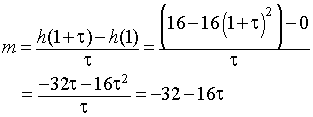|

|
Math 121 - Calculus for Biology I
Spring Semester, 2009
Velocity and Tangent Lines
|
|
|
|
© 1999, All Rights Reserved, SDSU &
Joseph M. Mahaffy
San Diego State University -- This page last updated
14-Mar-09
|
|

Velocity and Tangent
Lines
- Cats and
Gravity
- Falling Ball
Revisited
- Flight
of a Ball under Gravity
- Tangent
Line Interpretation
- Worked
Examples
- Applet for Derivative as
a Tangent Line
- Velocity of the Cat
- References
- An object falling under the influence of
gravity is a classical study in differential Calculus
Cats and Gravity


- Cat have evolved to be one of the best
mammalian predators
- Domestic cats have been shown to responsible
for up to 60% of the deaths of songbirds in some
communities
- They are adapted to hunting in
trees
- Cats have a very flexible spine for
hunting
- This flexibility allows them to rotate rapidly
during a fall
- Humans have been fascinated by this ability of
a cat to right itself
- Many scientific studies of cats falling
- One study of cats
falling out of New York apartments
showed that paradoxically the cats falling from the highest
apartments actually fared better than ones falling from an
intermediate height
- The cat remains tense early in the
fall
- With greater heights the falling cat
relaxes and spreads its legs to form a parachute
- This slows its velocity a little and
results in a more even impact
- From intermediate heights, the cat
basically achieves terminal velocity, but the tension causes
increased likelihood of severe or fatal injuries
- The early stages of the fall result from
acceleration due to gravity
- Newton's law of
motion says that
mass times
acceleration is equal to the sum of all the
forces acting on an
object
- Velocity is the derivative of
position
- Acceleration is the derivative of velocity
- Suppose that a cat falls from a branch that is
16 feet high
- The height of the cat satisfies the
equation
h(t) = 16 -
16t2.
- How long does this cat fall and what is its
velocity when it hits the ground?
- The first question is easily answered,
h(t) = 16 -
16t2 = 0,
which occurs when
t =
1
- However, the velocity at
t =
1 requires more work
- We will show that the cat has a velocity,
v(1) = -32
ft/sec (or about
21.8
mph)
Falling Ball Revisited
- Below is an applet showing
- The height of the ball as a function of
time,
h(t)
- The average velocity of the ball as a
function of time
- Recall that average velocity is the difference
in positions divided by time
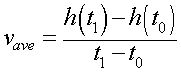
source
for dropspeed4a
Alternate link
- The height of the ball as a function of time
follows a parabolic path
- The distance of the ball between successive
flashes increases with time
- The velocity becomes more negative and follows
a straight line
- The derivative of a quadratic function will be
a linear function
Flight of a Ball under
Gravity
- Consider a ball thrown vertically under the
influence of gravity, ignoring air resistance
- The ball begins at ground level
(h(0) =
0 cm)
- It is thrown vertically with an initial
velocity, v(0) =
1960 cm/sec
- The acceleration of gravity is
g =
980 cm/sec2
- The height of the ball for any
time
t
(0 < t
<
4) is given by
h(t) = 1960
t - 490 t2
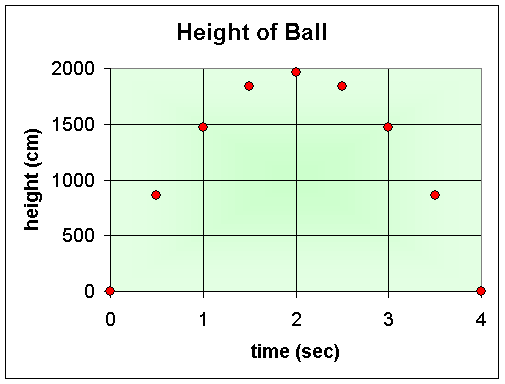
Height of the Ball
- The graph for the height of the ball
h(t)
over the first 4 seconds, showing the position of the ball at
every 0.5 sec
Velocity of the Ball
- Compute the average velocity between each
point on the graph
- The average velocity is the difference between
the heights at two times divided by the length of the time
period
- For convenience, associate the average
velocity with the midpoint between each time interval
considered
|
h(t1)
|
h(t2)
|
ta
= (t1+
t2)/2
|
Average Velocity
(h(t2)
- h(t1))/( t2 -
t1)
|
|
h(0) =
0
|
h(0.5) =
857.5
|
ta
= (0 + .5)/2 = 0.25
|
v(0.25) =
1715
|
|
h(1.5) =
1837.5
|
h(2) =
1960
|
ta
= 1.75
|
v(1.75) =
245
|
|
h(3) =
1470
|
h(3.5) =
857.5
|
ta
= 3.25
|
v(3.25) =
-1225
|
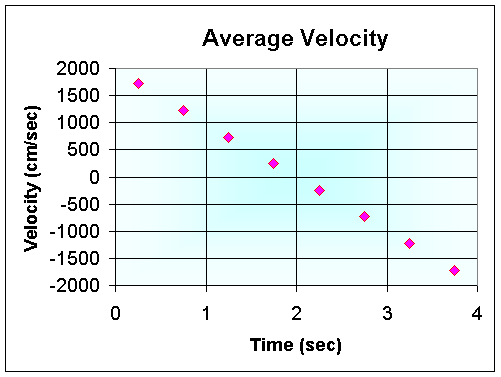
- A graph of the average velocities is
below
- The graph of the average velocities is a
straight line
- The average velocity is zero when the ball
reaches its maximum height
- The velocity should be zero when the ball is
at the top of its flight
- Consider the graph of the height with data
every 0.1 sec
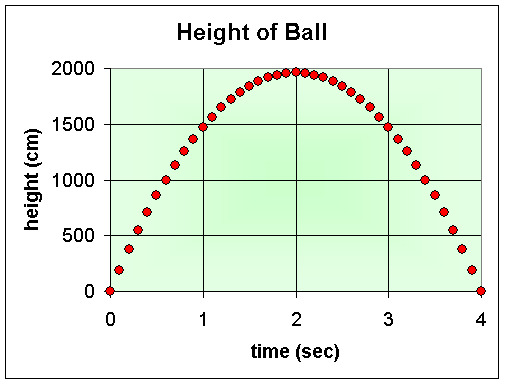
- How does this affect the average velocity
computation?
- The distance between successive heights is
now closer
- But then the intervening time interval is
also closer together
- The average velocity between
t1 = 0.2
and
t2 =
0.3 has
h(t1)
= 372.4 cm and
h(t2)
= 543.9 cm, so
v(0.25) =
1715 cm/sec, the same as before
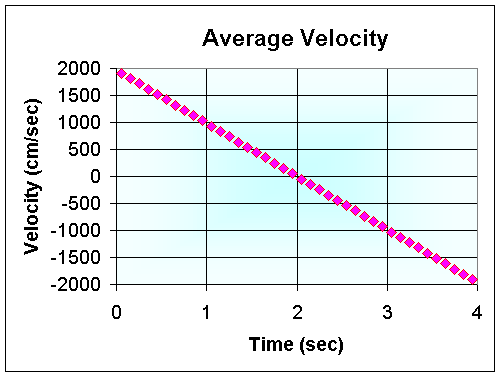
- The average velocity data lie on the same
straight line as before
v(t) = 1960 -
980 t
- This straight line function is the
derivative
of the quadratic height function
h(t)
- The calculation suggests that the derivative
function is independent of the length of the time interval chosen;
however, this was specific to the quadratic nature of the height
function
- We will learn in the coming sections how to
take derivatives of more functions.
Tangent Line
Interpretation
- The average velocity is the same calculation
as the slope between the two data points of the height
function
- The
slope of the secant
line between two points on a curve
- Geometrically, as the points on the curve get
closer together, then the secant line approaches the tangent
line
- The
tangent line represents the best
linear approximation to the curve near a given point
- Its slope is the derivative of the function at
that point
Example:
Consider the function
y =
x2
- Find the equation of the
tangent
line at the point
(1,1)
on the graph
- A
secant
line
is found by taking two points on the
curve and finding the equation of the line through those
points
- The animated gif below shows a
sequence of secant lines
that converge to the tangent line by taking
the two points closer and closer together
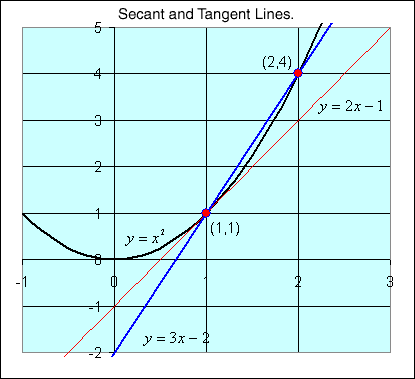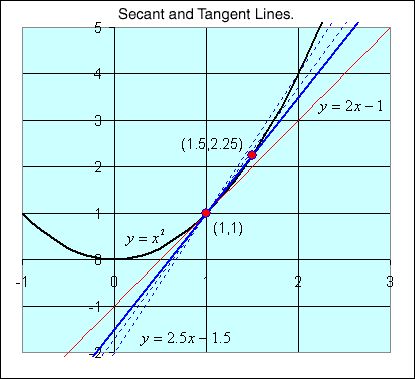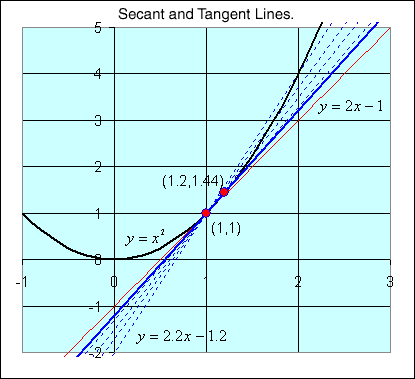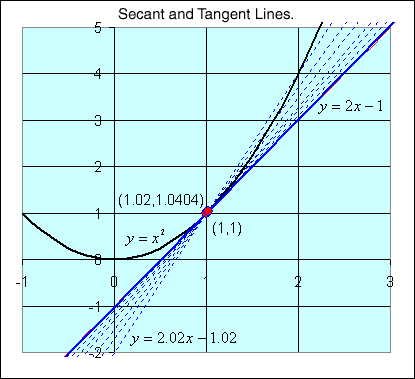
- Consider the secant line through the points
(1,1)
and
(2,4)
- This line has a slope of
m =
3, and its equation is
y = 3x -
2
- Next consider the pair of points on the curve
y =
x2,
(1,1)
and
(1.5, 2.25)
- This line has a slope of
m =
2.5, and its equation is
y = 2.5x -
1.5
- The secant line through the points
(1,1)
and
(1.1, 1.21) has a slope of
m = 2.1
- Its equation is
y = 2.1x -
1.1
General secant line for
y =
x2 at
(1,1)
- Consider the x
value x = 1+ h
for some small h
- The corresponding y
value y = (1+ h)2
= 1 + 2h
+ h2
- The slope of the secant line through this point and the
point (1,1) is
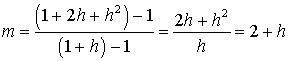
- The formula for this secant line
is
y = (2+h)x
- (1+h)
- As h gets
very small, the secant line gets very close to the tangent line
- Its not hard to see that the tangent line for y
= x2 at (1,1)
is
y = 2x -
1
- The slope of the tangent line,
m =
2, is the value of the derivative of
y =
x2 at
x =
1.
Applet for Interpreting the Derivative as
the Slope of the Tangent Line
- The tangent line can be found by taking a
sequence of secant lines with the
x
values getting closer together
- These calculations are clearly very
tedious
- The geometric view of the tangent line is very
easy to visualize
- Our applications relate the derivative to
growth rate and velocity and are simply the slope of the tangent
line
- Below is an applet for exploring the
derivative of a cubic function (left)
- Its derivative is on the right
- Click on the figure on the
left and a point with the tangent line will appear on the
graph
- The value of the slope of the
tangent line appears in the graph on the right
source
for slope3c
Alternate link
Several points of particular interest
- The graph on the left is a cubic function,
while the graph of its derivative is a quadratic
- As you approach a maximum (or minimum) for the
cubic function, the value of the derivative goes to zero and the
sign of the derivative function changes
- This is an important application of the
derivative
Velocity of the
Cat
- Our example of a cat falling from a
branch that is 16 feet high satisfies the equation
h(t) = 16 -
16t2.
- The cat hits the ground ofter only one second
of falling
- To find the velocity of the cat, we need to
determine its the slope of the tangent line for
h(t)
near t =
1.
- Find the height for a small increment of time after t
= 1, say t
= 1 + t
- The slope of the secant line between the heights at t
= 1 and t
= 1 + t
is
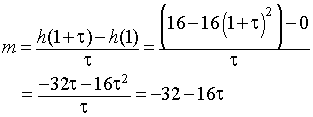
- The velocity at t
= 1 is the slope of the tangent line
- Let t
go to zero, then the velocity of the cat at t
= 1 is
v(1) = -32
ft/sec (or about
21.8
mph).
References:
[1] Jared M. Diamond (1988), Why cats have
nine lives, Nature 332, pp 586-7.