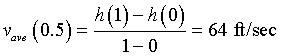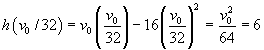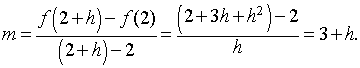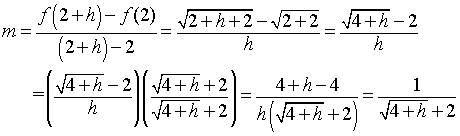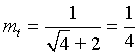|

|
Math 121 - Calculus for Biology I
Spring Semester, 2004
Velocity and Tangent Lines - Examples
|
|
|
|
© 1999, All Rights Reserved, SDSU &
Joseph M. Mahaffy
San Diego State University -- This page last updated
24-Apr-01
|
|

Velocity and Tangent Lines
- Examples
-
- Flight of a Ball
- Climbing a Salmon Ladder
- Sequence of Secant Lines
- Secant Line with h
- Another Secant Line with h
Example 1
(Flight of a
Ball):
- A ball, which is thrown vertically with an
initial velocity of 80 ft/sec and only the acceleration of gravity
acting on the ball, satisfies the equation:
h(t) =
80t - 16t2
a. Sketch a graph of the height of the ball (in
feet),
h(t),
showing clearly the maximum height and when the ball hits the
ground.
b. Find the average velocity of the ball between
t =
0 and
t =
1 and associate this velocity with
t =
0.5. Repeat this process for each second of
the flight of the ball, then sketch a graph of the average velocity
as a function of time,
t.
Solution:
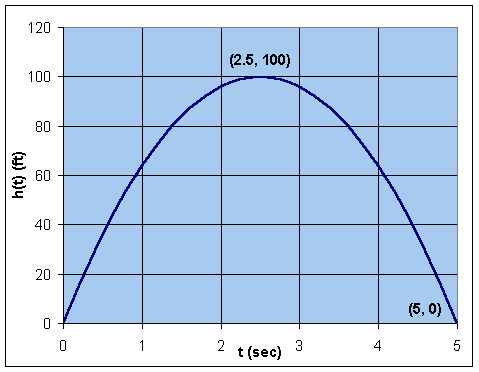
a.
- The graph of
h(t)
is a parabola with
t-intercepts
at t =
0 and
t = 5
- Thus, the ball hits the ground at
t = 5
- The vertex or maximum height of the ball
occurs at the midpoint between these intercepts or
t = 2.5
with
h(2.5) = 100
ft
- Below is a graph showing the height of the
ball as a function of
t
b.
- The average velocity for the ball between
t =
0 and
t =
1 sec is
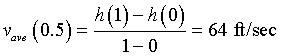
- Similarly, the average velocities are computed
between each pair of seconds from
t =
0 to
t = 5
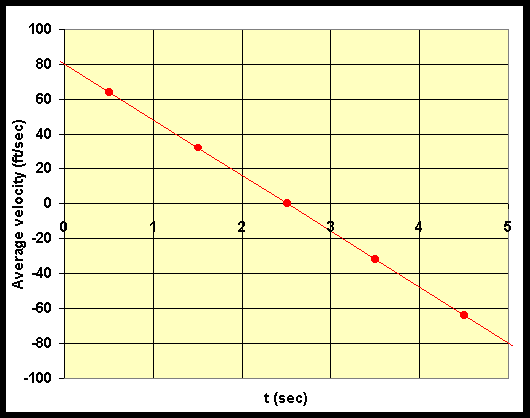
|
t
|
0.5
|
1.5
|
2.5
|
3.5
|
4.5
|
|
vave
|
64
|
32
|
0
|
-32
|
-64
|
- The graph of the average velocity is a
straight line
- Note that the average velocity is zero at the
maximum of the height curve,
h(t)
Example
2(Leaping Salmon):
- A river is dammed, and a salmon ladder is
built to enable the salmon to bypass the dam and continue to
travel upstream to spawn
- The vertical walls on the salmon ladder are 6
feet high
- The salmon has to leap vertically upwards over
the wall
- The height of the salmon during its leap is
given by
h(t) =
20t - 16t2.
a. Sketch a graph of the height of the salmon (in
feet),
h(t),
with time, showing clearly the maximum height and when the salmon can
clear the wall.
b. Find the average velocity of the salmon between
t =
0 and
t =
0.5 and associate this velocity with
t =
0.25. Repeat this process for each half-second
of the leaping salmon, then sketch a graph of the average velocity as
a function of time,
t.
c. Determine the minimum speed,
v0,
that the salmon needs on exiting the water to climb the salmon ladder
if the height is given by the formula
h(t) =
v0t -
16t2.
Solution:
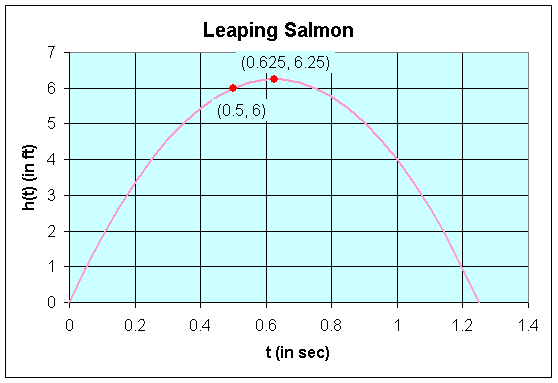
a.
- The function
h(t)
is a parabola,
h(t) =
20t - 16t2 = 4t(5 -
4t).
- The
t-intercepts
are t =
0 and
t = 5/4 =
1.25
- The vertex occurs at
(0.625, 6.25)
The salmon can clear the wall when
h(t) =
6, so
20t - 16t2
= 6 or
8t2 -
10t + 3 = 0. This can be factored to
give
(2t - 1)(4t -
3) = 0.
It follows that either
t =
1/2 or
t =
3/4, so the salmon can clear the wall at any
time 1/2 < t
< 3/4 sec.
The graph of this parabola is seen
below.
b. The average velocity of the salmon between
t =
0 and
t =
0.5 is given by
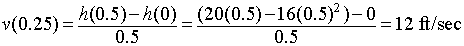
Similarly, the average velocity of the salmon
between t =
0.5 and
t =
1 is given by
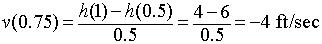
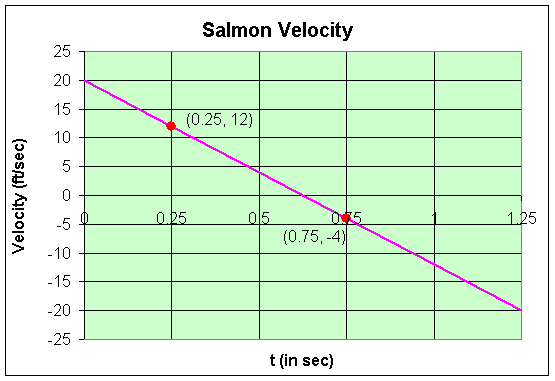
The graph of the velocity curve is
below
c. The minimum speed,
v0,
that the salmon needs to climb the fish ladder is the one that
produces a maximum height of 6
ft. This is equivalent to having the vertex of
the height function occur with
h =
6. Since
h(t) =
v0t -
16t2, the
t-value
of the vertex occurs at
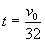
(since this is halfway between the
intercepts t =
0 and
t = v0
/16). Since we want the vertex to be
6 ft,
we need to satisfy the equation
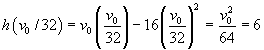
Thus,
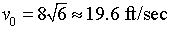
Example 3
(Secant Lines):
- Form a
sequence of secant
lines with pairs of points on the
curve,
f(x)
- Consider the function
f(x) =
x2 -
x.
a. Let one point on all secant lines have
x =
1. The other points in the sequence have
x =
2,
x =
1.5,
x =
1.2,
x =
1.1, and
x = 1.01.
Find the sequence of secant lines with these
points on the lines and on
f(x).
b. The derivative of
f(x)
is the slope of the tangent line. As the
values of
x
get closer together, the secant lines approach the tangent line. Use
the results in Part a. to determine the equation of the tangent line
through the point (1,
0), and from its slope find the derivative of
f(x).
c. Graph
f(x),
the tangent line, and the secant lines.
Solution:
a. The left point for all the secant lines is
(1, 0)
- When
x =
2, the other point is
(2, 2)
- The equation of a line through
(1,
0) and
(2,
2) has a slope of
2
and
y-intercept
of
-2,
so
y = 2x -
2
- For
x =
1.5, the points on the secant line (and
f(x))
are (1,
0) and
(1.5, 0.75)
- This secant line has a slope of
m = (0.75 -
0)/(1.5 - 1) = 1.5
- It follows that the equation for this secant
line is
y = 1.5x -
1.5
- For
x =
1.2, the points on the secant line (and
f(x))
are (1,
0) and
(1.2, 0.24)
- This secant line has a slope of
m = (0.24 -
0)/(1.2 - 1) = 1.2
- The equation for this secant line
is
y = 1.2x -
1.2
- For
x =
1.1, the points on the secant line (and
f(x))
are (1,
0) and
(1.1, 0.11)
- This secant line has a slope of
m = (0.11 -
0)/(1.1 - 1) = 1.1
- The equation for this secant line
is
y = 1.1x -
1.1
- For
x =
1.01, the points on the secant line (and
f(x))
are (1,
0) and
(1.01, 0.0101)
- This secant line has a slope of
m = (0.01 -
0)/(1.01 - 1) = 1.01
- The equation for its secant line
is
y = 1.01x -
1.01
b. The sequence of secant lines is converging to
the tangent line
y = x -
1
- The slope of this line is
1,
so the derivative of
f(x) =
x2 - x at
x =
1 is also
1
c. Below is a graph of the function, the tangent
line, and our secant lines.
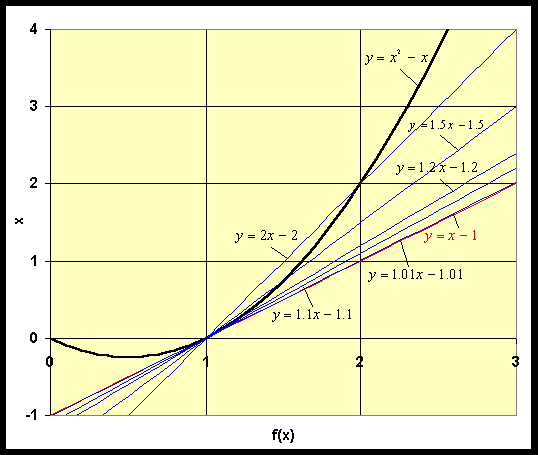
- It becomes tedious calculating each of the elements of the
sequence of secant lines
- The more general way to compute a secant line for a function
f(x)
at a point x
is to find the equation of a line through the points (x,
f(x)) and (x+
h, f(x+h)),
where h
is some value different than zero
Example 4 (Secant line with h):
Suppose we take the previous example and find the equation
of the secant line through the points (2,
f(2)) and (2+
h, f(2+h),
where
f(x) =
x2 -
x.
Let Dx
get small and determine the slope of the tangent line through
(2, 2),
which gives the value of the derivative of
f(x)
at
x =
2.
Solution:
f(2+h)
= (2+h)2
- (2+h)
= 4 + 4h
+ h2
- 2 - h
= 2 + 3h
+ h2
- The slope of the secant line is
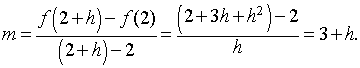
- The point slope form of the line (with the
point (2,
2) on the secant line) gives
y - 2 = (3 + h)(x
- 2)
y = (3 + h)x - 4 - 2
h
- As h
approaches zero, the secant line approaches the tangent line
y = 3x -
4
- This line has a slope of
3,
so the derivative of
f(x)
at
x =
2 must be
3.
Example 5 (Secant line for a
Square Root):
- Consider a more complicated
function
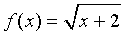
- Find the slope of the secant line through the points (2,
f(2)) and (2+
h, f(2+h))
- Let h
get small and determine the slope of the tangent line through (2,
2), which gives the value of the derivative of
f(x) at x
= 2
Solution:
- The slope of the secant line is
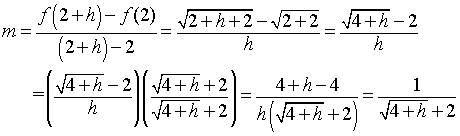
- This formula is substantially more
complex
- This shows that finding the slope of the
secant line can become quite tedious and difficult
- In the formula above, as h
approaches zero, the slope of secant line, m,
approaches
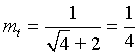
- Since the derivative is related to the
limiting case of the slope of the secant lines (the slope of the
tangent line, mt),
we see that the derivative of
f(x)
at
x =
2 must be
1/4