![]()
Math 121 - Calculus for Biology I
Spring Semester, 2004
Quotient Rule
San Diego State University -- This page last updated 10-Jan-04
|
|
Math 121 - Calculus for Biology I |
|
|---|---|---|
|
|
San Diego State University -- This page last updated 10-Jan-04 |
|
In this section, we examine the kinetics of hemoglobin molecules for carrying O2 to the cells of the body. A quotient rule is developed to examine the maximum rate of change in O2 affinity. In earlier sections, we studied graphing of rational functions, but had no techniques for finding critical points. The ability to find the derivatives of rational functions allows locating minima and maxima of these functions.
Hemoglobin is the most important molecule in our erythrocytes (red blood cells). For mammals, this very important compound has evolved to carry O2 from the lungs to the tissues and remove CO2 from the tissues back to the lungs. For adult humans, the hemoglobin molecule consists almost exclusively of two a and two b polypeptide chains (there are other types of peptide chain such as g in fetal blood). Each polypeptide chain contains a porphyrin ring with iron near the active binding site. The four polypeptide chains fold into a quaternary structure that has evolved to very efficiently bind up to four molecules of O2. A single mutation causes the disease sickle cell anemia, where structure of one b chain is varied and distorts the binding efficiency, so O2 transport is diminished.
Oxygen is key to efficient metabolism and is required by all of our cells. The hemoglobin molecule takes advantage of cooperative binding to effectively load and unload O2 molecules from the blood to the cells in the tissues. In cooperative binding, the binding of one molecule facilitates the binding of one or more other molecules by causing structural changes to the protein. Cooperative binding plays a role in many biochemical processes where a steep dissociation curve is needed in the equilibrium kinetics. This cooperative binding results in a variant form of the Michaelis-Menten velocity curve that we studied in an earlier section and takes on a characteristic S-shape that results in a protein having more of an on/off function in its kinetic properties. The steepness in the dissociation curve is needed for effective O2 exchange. Where the dissociation curve is steep, a small partial pressure difference in the concentration of O2 results in easy unloading of O2 at the tissues. In the lungs, the O2 readily loads onto the hemoglobin molecules, while a different dissociation curve allows the removal of CO2.
Oxygen affinity of hemoglobin is important in understanding the gas-transport properties of this molecule. Ranney and Sharma [2] give the kinetic dissociation curve for hemoglobin under a variety of conditions. Typical of most kinetic reactions, the dissociation curve for hemoglobin is highly sensitive to pH, temperature, and other factors. Oxygen affinity is usually expressed by a dissociation function that measures the percent of hemoglobin in the blood saturated with O2 as a function of the partial pressure of O2. (The partial pressure of O2 is often measured in torrs where 100 torrs is the atmospheric concentration of O2.) The fraction of hemoglobin saturated with O2 satisfies the function
![]()
where y is the fraction of hemoglobin saturated with O2 and P is the partial pressure of O2 measured in torrs. The Hill coefficient is n in the expression above, representing the number of molecules binding to the protein, while K is the binding equilibrium constant. Typically, hemoglobin shows a nonlinear form that has a Hill coefficient of 2.7-3.2 though it can bind cooperatively up to 4 molecules of O2. Under conditions typical of blood, experimental measurements show that the values of n and K are 3 and 19,100, respectively. Below we see a graph of this O2 saturation curve.
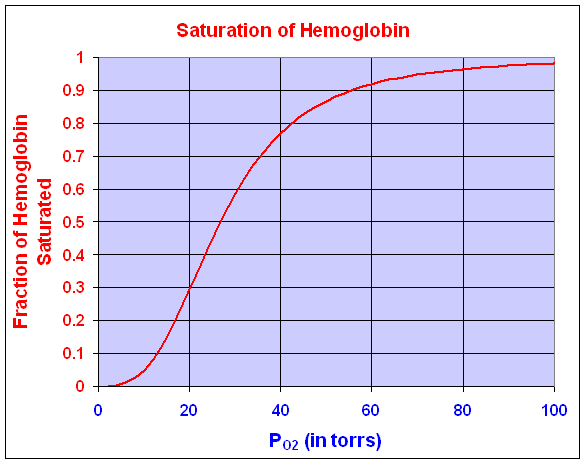
Where the dissociation curve is steepest, the O2 binds and unbinds to hemoglobin over the narrowest changes in partial pressure of O2. This allows the most efficient exchange of O2 in the tissues. That is, when a tissue is low in O2, then the hemoglobin in the blood is more likely to have its O2 dissociate and diffuse into the O2 depleted cell. This steepest part of the dissociation curve is where the derivative is at its maximum. Clearly, evolution is likely to choose an animal that has hemoglobin with a dissociation curve that matches the steepest part of the curve to the existing partial pressure of O2 near the tissues. For our dissociation curve given above, we want to find where the derivative is largest. This corresponds to the point of inflection for this curve. Since the curve is defined by a rational function, we need to develop a quotient rule to find its derivative.
Let f(x) and g(x) be two differentiable functions. The quotient rule for finding the derivative of the quotient of these two functions is given by:
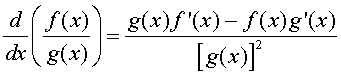
where f '(x) and g'(x) are the derivatives of the respective functions. In words, the quotient rule says that the derivative of the quotient is "the bottom times the derivative of the top minus the top times the derivative of the bottom all over the bottom squared."
Example: Suppose we want to study the function
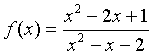
We can apply the quotient rule to this function to find its derivative. We obtain
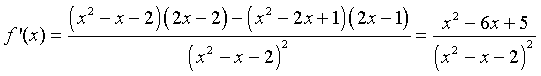
For graphing this function, we would like to find intercepts, asymptotes, and extrema. The y-intercept is given by y = f(0) = -1/2. The x-intercept is found by solving f(x) = 0. This is solved by setting the numerator equal to zero, but
which gives the x-intercept as x = 1.
The vertical asymptotes are found finding when the denominator is zero, so
This gives the vertical asymptotes x = -1 and x = 2. The horizontal asymptote is found by looking at f(x) for large values of x. The largest exponents in the numerator are both 2, so for large x, f(x) behaves like x2/ x2 = 1, which gives the horizontal asymptote y = 1.
The critical points are found by setting the derivative equal to zero, which again requires setting the numerator equal to zero. Thus,
Thus, the critical points are xc = 1 and xc = 5. Evaluating the function f(x) at these critical points, and we find a local maximum at (1, 0) and a local minimum at (5, 8/9). A graph of this function is seen below.
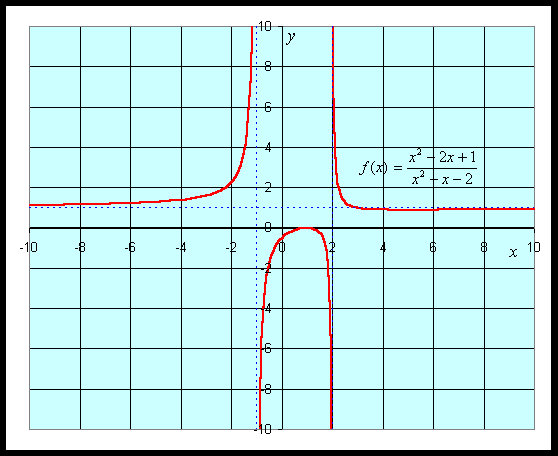
See more graphing examples in the Worked Examples.
Dissociation Curve for Hemoglobin
The dissociation curve for O2 with hemoglobin is shown above. The specific function that was graphed was
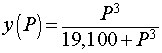
We want to determine the partial pressure of O2 that results in the steepest part of the curve above. To find the slope of the curve, we compute the derivative using the quotient rule. The derivative satisfies
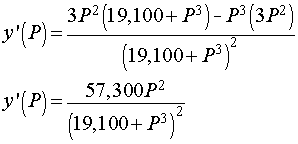
Below is the graph of this derivative
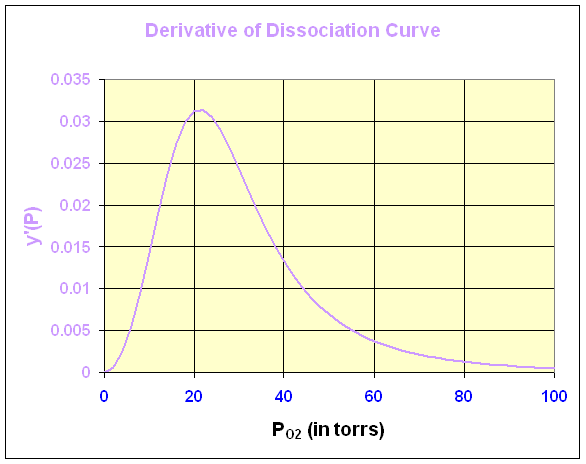
We can see that the maximum derivative occurs at about PO2 = 21 torrs. To find the exact value of the maximum derivative, we compute the second derivative and set it equal to zero. The second derivative is given by
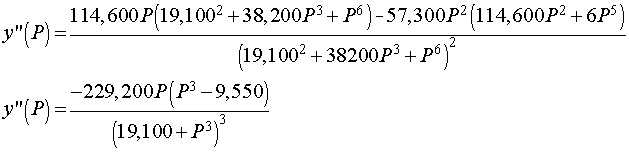
The last expression requires some algebra or Maple to derive from the first. The second derivative is equal to zero when either P = 0 or 95501/3 = 21.22. Thus, the point of inflection, which is where the derivative is at a maximum, occurs at P = 21.22 with y(P) = 0.333 or about 1/3 of the hemoglobin is saturated by O2.
Multicellular organisms begin with exponentially growing cell populations (Malthusian growth), but soon must regulate this cell growth to develop particular patterns and shapes and differentiate their cells into organs with specific functions. The adult organism maintains a fairly constant number of cells, which means that cells must recognize whether or not there is a need to divide, a process known as mitosis. Cancer is often the breakdown of this control, with cells dividing when they normally would not. One significant question that has yet to be adequately answered is how a cell, such as a skin cell, recognizes its neighboring environment of other cells and knows whether or not it should divide. (A skin cell obviously needs to undergo mitosis when either wear or damage of the skin requires replacement cells.)
The regulation of mitosis is a very important biological process that is currently being studied extensively. This research tries to understand how cells determine when they should undergo mitosis. One controversial biochemical theory developed in the late 1960s was that cells communicated with neighboring cells by tissue-specific inhibitors known as chalones [1]. The chalones are released by cells and diffuse in the environment to affect the cells nearby. If there are sufficient quantities of these chalones, then cells are inhibited from undergoing mitosis.
One of the proposed mechanisms is that chalones bind specifically to certain proteins involved in mitosis. The chalones inactivate the mitotic proteins, leaving the cell in a quiescent state. This inhibition process of effector molecules binding to a protein is often modeled using a Hill function with a special rational form. Let Pn represent a certain cell density at a particular time n, then an appropriate mathematical model for the cell density at the next time period (Pn+1) that considers the mitotic divisions and cell loss that are dependent on the cellular density with inhibition due to crowding is given by the following equation:
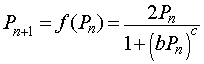
where b and c are parameters that are fit to data based on chalone kinetics. The function f(Pn) is known as an updating function, which will be studied in more detail in a future section. Notice that when the cell density Pn is very low, then the denominator of the model is insignificant. This gives the equation Pn+1 = 2Pn, so for low density the population doubles in each time period, using a standard discrete Malthusian growth model.
Let us study the specific mitotic model given by the equation
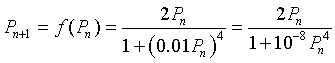
We would like to determine what the cell density is at equilibrium, which is when the cell density remains constant for all time intervals. Thus, the new cells produced match the numbers that are lost in a given time interval. In addition, we would like to graph the updating function f(Pn) and give some biological interpretations of the graph.
Equilibria of the Mitotic Model
At equilibrium, the population density is the same at all time intervals. Thus, Pn+1 = Pn = Pe, which when substituted into the equation above gives
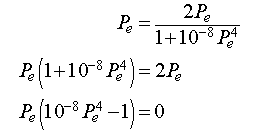
Thus, either Pe = 0 or Pe = 100. The first equilibrium is when the trivial equilibrium when no cells exist, while the second equilibrium would ideally be the preferred density of cells in a particular tissue.
Graphing the Mitotic Updating Function
To study the graph of f(Pn), we examine the intercepts, asymptotes, and any extrema. Clearly, the only intercept is (0, 0), passing through the origin. The denominator is always positive, so there are no vertical asymptotes. We also see that the power of Pn in the denominator is 4, which exceeds the power of Pn in the numerator. This implies that as Pn gets sufficiently large, the denominator gets larger than the numerator much faster, so there is a horizontal asymptote at y = 0.
To find any extrema, we differentiate f(Pn), which gives
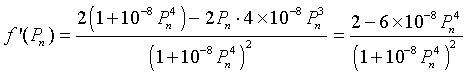
Setting this derivative equal to zero, we have
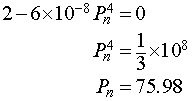
It follows that the maximum of the updating function occurs at (75.98, 113.98). Below we see a graph of the updating function.
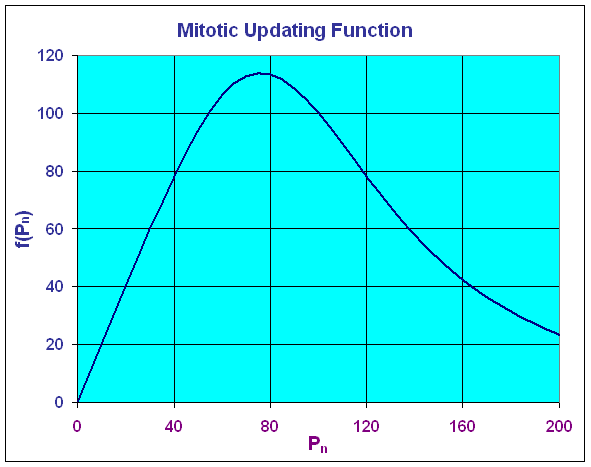
The graph above shows that the greatest production of cells occurs at a cell density of 75.98, then it declines fairly rapidly. At a cell density of Pn = 100, the production equals the number dying so the model is at equilibrium. If one were to have a fairly high density, then this model would predict a toxic effect from the crowding, resulting in a major die-off so that the next time period would have a very low density. This model is clearly very simplistic, but it does demonstrate some of the important concepts behind biochemical inhibition.
[1] W. S. Bullough and E. B. Laurence (1968) Chalones and cancer, Nature 220, 134-135.
[2] H. M. Ranney and V. Sharma, Structure and function of hemoglobin, in Willliam's Hematology, eds. E. Beutler, M. A. Lictman, B. S. Coller, T. J. Kipps, 5th Edition, 1995, p. 417-425.