![]()
Math 121 - Calculus for Biology I
Spring Semester, 2004
Quotient Rule - Examples
San Diego State University -- This page last updated 12-Jan-04
|
|
Math 121 - Calculus for Biology I |
|
|---|---|---|
|
|
San Diego State University -- This page last updated 12-Jan-04 |
|
Below we present several examples to demonstrate the quotient rule. The examples begin with differentiation and graphing, then an example from biochemical kinetics is shown.
Differentiation - Quotient Rule
Below are two functions for using the rules of differentiation. The second function relates to the continuous version of the logistic growth model.
Example 1: Differentiate the following functions:
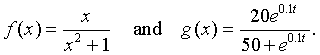
Solution: The quotient rule is applied to each of these functions.
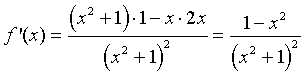
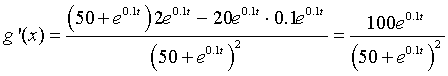
Example 2: Consider the function:
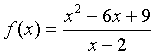
Differentiate this function. Find all intercepts, asymptotes, and extrema. Graph the function.
Solution: The quotient rule for differentiation is applied to f(x) yielding
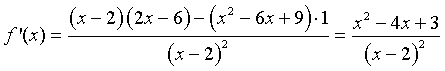
The y-intercept is given by y = f(0) = -9/2. The x-intercept is found by solving f(x) = 0. This is solved by setting the numerator equal to zero, but
which gives the x-intercept as x = 3.
The vertical asymptotes are found finding when the denominator is zero, so a vertical asymptote occurs at x = 2. There are no horizontal asymptotes as the power of the numerator exceeds the power of the denominator.
The critical points are found by setting the derivative equal to zero, which again requires setting the numerator equal to zero. Thus,
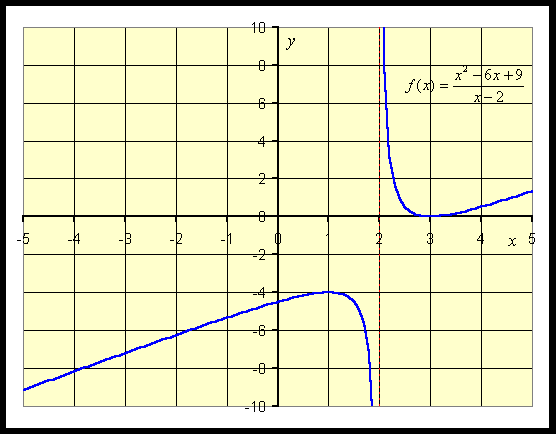
Thus, the critical points are xc = 1 and xc = 3. Evaluating the function f(x) at these critical points, and we find a local maximum at (1, -4) and a local minimum at (3, 0). A graph of this function is seen below.
Example 3: In 1960, Jacob and Monod won a Nobel prize for their theory of induction and repression in genetic control. Many metabolic pathways in cells use endproduct repression of the gene or negative feedback to control important biochemical substances, such as the enzymatic pathways for production of amino acids. When sufficient quantities of a particular substance, such as an amino acid, the cell shuts down the pathway that produces that substance to avoid unnecessary build up of the substance. From biochemical kinetics, it can be shown that production of a substance x satisfies a rate function of the following form:
![]()
Consider the specific rate function given by
![]()
Differentiate this rate function. Sketch a graph of this rate function and its derivative. Find all intercepts, any asymptotes, and any extrema for the rate function and its derivative. When is the rate function decreasing most rapidly?
Solution: The rate function has an R-intercept, R(0) = 90/27 = 10/3. There is a horizontal asymptote of R = 0, since the power of the denominator exceeds that of the numerator. From the quotient rule, the derivative satisfies
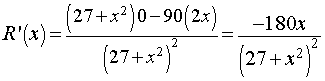
For x > 0, the derivative of the rate function is negative, so this is decreasing. There is clearly a maximum at x = 0. (A rate function doesn't make sense for x < 0. Below is a graph of the rate function.
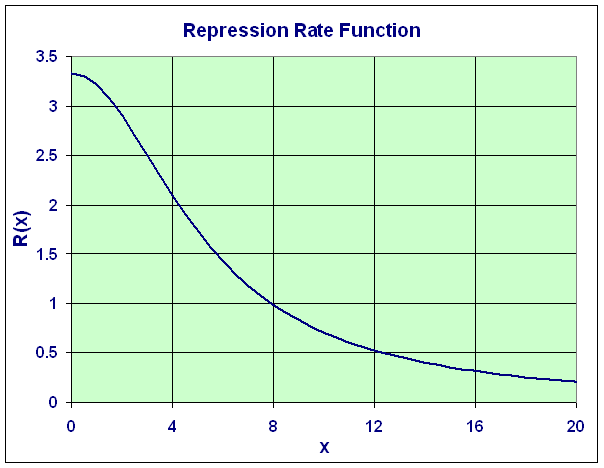
The derivative has an intercept at (0, 0) and also has a horizontal asymptote R' = 0. To find any extrema of the derivative function, we find the second derivative. Since the derivative can be written,
![]()
The second derivative is given by
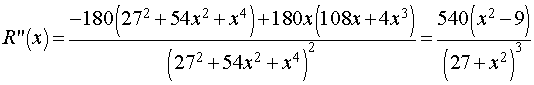
where some algebra is required for the last quantity. Clearly, this second derivative is zero when x = 3 (x = -3 is outside the domain). Thus, R' (x) has a minimum at (3, -5/12). Below is a graph of the derivative of the repression rate function.
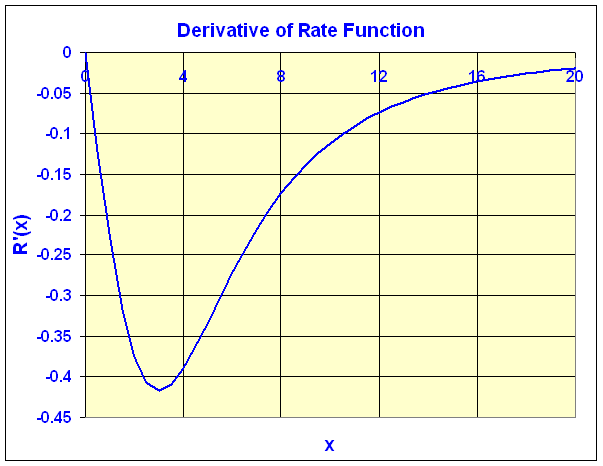
It follows that the original rate function is decreasing most rapidly at x = 3.