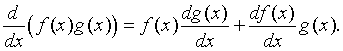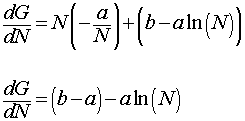Math 121 - Calculus for Biology I Spring Semester, 2004 Product Rule
	© 2001, All Rights Reserved, SDSU & Joseph M. Mahaffy San Diego State University -- This page last updated 04-Jan-04

 
1. Gompertz Model for Tumor Growth
2. Product Rule
3. Worked Examples
4. Ricker's Growth Function
5. References

Gompertz Model for Tumor Growth

• Tumors grow based on the nutrient supply available
• Tumor angiogenesis is the proliferation of blood vessels that penetrate into the tumor to supply nutrients and oxygen and to remove waste products
• The center of the tumor largely consists of dead cells, called the necrotic center of the tumor
• The tumor grows outward in roughly a spherical shell shape

• Simpson-Herren and Lloyd (1970) studied the growth of tumors
• They studied the C3H Mouse Mammary tumor
• Ttritiated thymidine was used to measure the cell cycles
• This gave the growth rate for these tumors

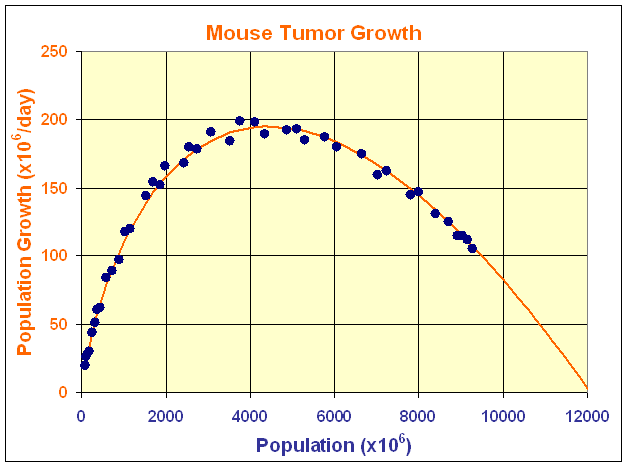
• Below is a graph showing the population of tumor cells and the growth rate of the tumor at the various sizes of the tumor
• The graph includes the curve for the Gompertz model

• Laird (1964) showed that tumor growth satisfies Gompertz growth equations

G(N) = N(b - a ln(N))

• Where N are the number of tumor cells and a and b are constants matched to the data
• This function is not defined for N = 0
• For the data above, the best fit curve is

G(N) = N(0.4126 - 0.0439 ln(N))

• The growth of the tumor stops at equilibrium
• The tumor is at its maximum size supportable with the available nutrient supply
• We also want to know when the tumor is growing most rapidly
• This occurs when the derivative is zero

• The equilibrium is

G(N) = N(b - a ln(N)) = 0

• Since N > 0, this occurs when b - a ln(N) = 0

ln(N) = b/a

N_e = e^b/a

• Thus, N_e = e^b/a is the unique equilibrium (carrying capacity)
• For the specific data above, the

N_e = e^{0.4126/0.0439} = = e^9.399 = 12,072

• Which matches the P-intercept on the graph above

• Finding the derivative of G(N) presents a new problem in differentiation
• We need the product rule for differentiation to differentiate G(N)

Product Rule

• Let f(x) and g(x) be differentiable functions. The product rule for finding the derivative of the product of these two functions is given by:

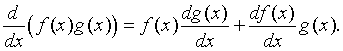
• In words, this says that the derivative of the product of two functions is the first function times the derivative of the second function plus the second function times the derivative of the first function

Example 1: Consider f(x) = x⁵

• We know that f '(x) = 5x⁴
• Let f₁(x) = x² and f₂(x) = x³, then f(x) = f₁(x) f₂(x)
• From the product rule we have

Maximum Growth for the Gompertz Tumor Growth Model

• Apply the Product Rule to the Gompertz Growth function

G(N) = N(b - a ln(N)),

• The derivative is

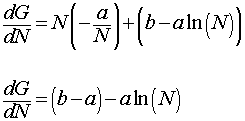
• The maximum occurs when G '(N) = 0,

a ln(N_max) = b - a.

N_max = e^{(b/a - 1)}.

• Applied to the Gompertz model for the mouse mammary tumor, then the maximum occurs at the population

N_max = e^{(9.399 - 1)} = 4,441 (x10⁶).

• Substituted into the Gompertz growth function, the maximum growth of mouse mammary tumor cells is

G(N_max) = 4441(0.4126 - 0.0439 ln(4441)) = 195.0 (x10⁶/day).

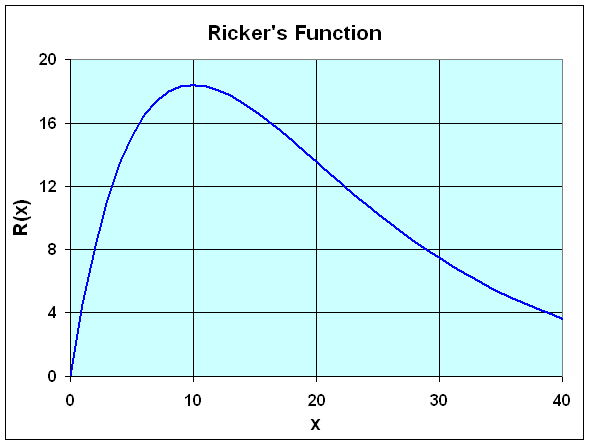
Example 2: Consider the Ricker function R(x) = 5x e^-0.1x

• Sketch a graph of this function, finding all extrema and points of inflection

Solution: The only intercept is the origin, (0, 0)

• The product rule gives

• Since the exponential function is never zero, R '(x) = 0 implies that the only critical point satisfies

1 - 0.1x = 0 or x = 10

• There is a maximum at (10, 50 e^-1) or (10, 18.4)

• Next the second derivative or the derivative of R '(x) gives

• The point of inflection is found by solving R ''(x) = 0
• The point of inflection occurs at x = 20

(20, 100 e^-2) or (20, 13.5)

Worked Examples

References

[1] A. K. Laird (1964), Dynamics of tumor growth, Brit. J. Cancer 18, 490-502.

[2] L. Simpson-Herren and H. H. Lloyd (1970), Kinetic parameters and growth curves for experimental tumor systems, Cancer Chemother. Rep. Part I, 54, 143-174.