Untitled Document

Math 121 - Calculus for Biology I
Spring Semester, 2004
Product Rule - Examples

© 2001, All Rights Reserved, SDSU & Joseph M. Mahaffy
San Diego State University -- This page last updated 04-Jan-04

Product Rule - Examples

Differentiation of Functions with a Product
Application to Graphing
Gompertz's Growth Model

Differentiation of Functions with a Product

Example 1: Consider the function

f(x) = (x³ - 2x)(x² + 5)

Find the derivative of f(x) by using the product rule. Next multiply the terms in f(x), then take the derivative of the resulting polynomial. Show that these give the same functions, verifying the product rule.

Solution: The product rule is carried out by multiplying the first term times the derivative of the second term, plus the second term multiplied by the derivative of the first term.

f '(x) = (x³ - 2x)(2x) + (x² + 5)(3x² - 2)

= 2x⁴ - 4x² + 3x⁴ - 2x² + 15x² - 10

f '(x) = 5x⁴ + 9x² - 10

We should be able to obtain the same result by multiplying the terms in f(x) and then taking the derivative of the resulting polynomial.

f(x) = x⁵ + 5x³ - 2x³ - 10x = x⁵ + 3x³ - 10x

f '(x) = 5x⁴ + 9x - 10

Thus, it is easy to see that the two methods do indeed yield the same result.

Example 2: Consider the function given by

g(x) = (x² + 4) ln(x)

Find the derivative of g(x) by using the product rule.

Solution: Again we multiply the first term times the derivative of the second term and add the second term multiplied times the derivative of the first term. Recall that the derivative of the natural logarithm equals the inverse of the argument.

g'(x) = (x² + 4)(1/x) + [ln(x)](2x) = x + 4/x + 2x ln(x)

Application to Graphing

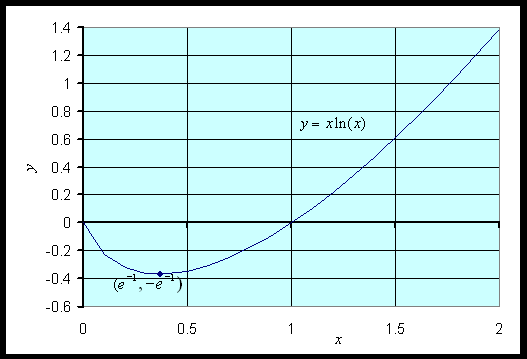
Example 3: Consider the function given by

f(x) = x ln(x)

Determine the domain of the function and find any intercepts. Find any critical points, then sketch the graph of f(x) for 0 < x < 2.

Solution:

The domain of the function is x > 0
There is no y-intercept
It can be shown that the limit as x tends to 0 from the right is 0
The x-intercept is found by solving f(x) = 0, which gives x = 1

To find the critical points we differentiate f(x) and set it equal to zero, giving

f '(x) = x(1/x) + ln(x) = 1 + ln(x) = 0

Thus, the critical value of x_c satisfies

ln(x_c) = -1 or x_c = e^-1~ 0.3679

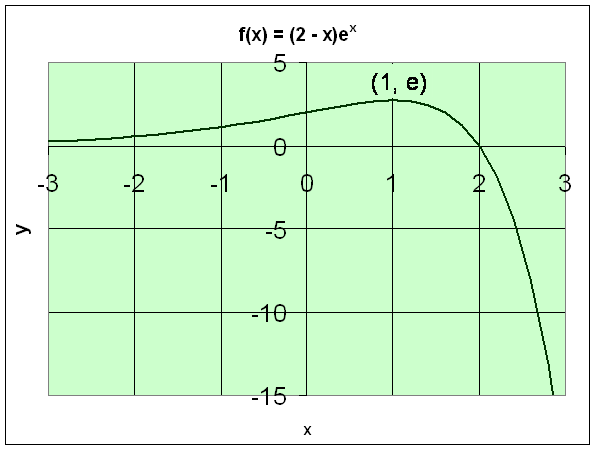
The function value at the critical point is f(e^-1) = - e^-1~ -0.3679
There is a minimum on the graph at (e^-1, - e^-1)

Example 4: Consider the function

f(x) = (2 - x)e^x.

Find the x and y-intercepts
Find any asymptotes
Find any critical points, then state if it is a local maximum or minimum
Sketch the graph of f(x)

Solution:

Since f(0) = 2, the y-intercept is (0, 2)
Since the exponential function is never zero, the x-intercept is (2, 0)
In the limit as x tends to , the exponential function goes to 0
An exponential function dominates any polynomial function
f(x) goes to 0, so there is a horizontal asymptote to the left.

The critical points are found by differentiating f(x) and setting it equal to zero,

f '(x) = (2 - x)e^x + (-1)e^x = (1 - x)e^x = 0.

The critical value of x_c is x_c = 1
The function value at the critical point is f(1) = e¹~ 2.718
There is a maximum on the graph at (1, e)
The graph of the function is seen below.

Example 4:

Suppose the the growth of a tumor is given by the Gompertz growth function

G(W) = W (0.5 - 0.05 ln(W)),

where W is the weight of the tumor in mg and the time units are days
Find the equilibrium weight of the tumor
Find the maximum growth rate for this tumor
Sketch the graph of G(W).

Solution:

The equilibrium is found by solving G(W) equal to zero, so

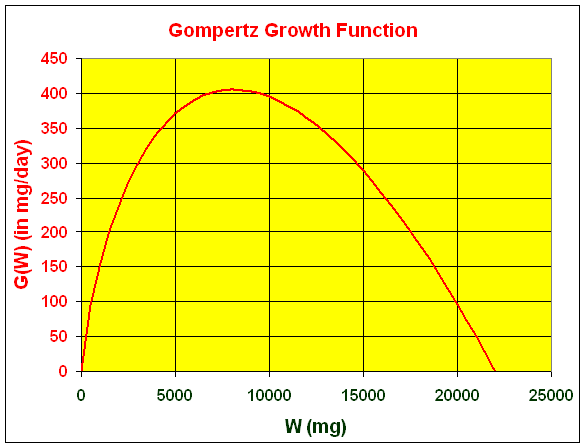
G(W) = W (0.5 - 0.05 ln(W)) = 0

0.5 - 0.05 ln(W) = 0

ln(W) = 10

W = e¹⁰ = 22,026 mg.

To find the maximum growth, we differentiate G(W),

G '(W) = W (- 0.05 (1/W) + (0.5 - 0.05 ln(W))

G '(W) = 0.45 - 0.05 ln(W) = 0.

ln(W) = 9

W = e⁹ = 8,103 mg.

with a maximum growth rate of

G(8,103) = 8,103(0.5 - 0.05 ln(8,103)) = 405.2 mg/day.

Below is a graph of this function