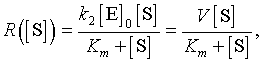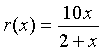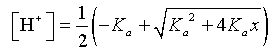1.  Michaelis-Menten Enzyme Kinetics
2. Polynomials and Rational Functions
3. Worked Examples
4. Acid Chemistry Revisited
5. Square Root Function
6. References

Michaelis-Menten Enzyme Kinetics

• Life forms are characterized by their distinct molecular composition, especially proteins
• Proteins are the primary building blocks of life
• Enzymes are proteins that facilitate reactions inside the cell
• Enzymes are noted for their specificity and speed under a narrow range of conditions
  • b-galactosidase catalyzes the break down of lactose into glucose and galactose
  • Urease rapidly converts urea into ammonia and carbon dioxide

• The simplest enzyme reaction follows the Michaelis-Menten mechanism
• Substrate, S, combines reversibly to the enzyme E to form a enzyme-substrate complex ES
• The complex decomposes irreversibly to form a product P
• The reaction is written as follows:

• The law of mass action is applied to these biochemical equations
• Differential equations are formed, which will be introduced later in the semester
• Simplifications allow easier understanding of the basic reactions
  • The enzyme-substrate complex forms extremely rapidly, creating a quasi-steady state
  • The forward reaction or turnover number, k₂, occurs on a slower time scale
  • The Michaelis-Menten reaction rate of the forward reaction to the product satisfies

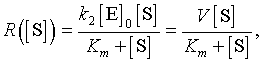
• where [S] is the substrate concentration and V and K_m are kinetic constants determined by the reaction given above
• The constant V (or V_max) is called the maximal velocity of the reaction
• K_m is the Michaelis constant, and its value is the value of the substrate concentration at which the reaction achieves half of the maximum velocity
• Note that the function R is a rational function.

Binding of ATP to Myosin

• Pate [1] shows that binding of ATP to myosin in forming cross-link bridges to actin for the power stroke of striated muscle tissue satisfies a Michaelis-Menten kinetics
• The reaction velocity is an actual velocity of motion, where the chemical energy of ATP is transformed into mechanical energy by movement of the actin filement
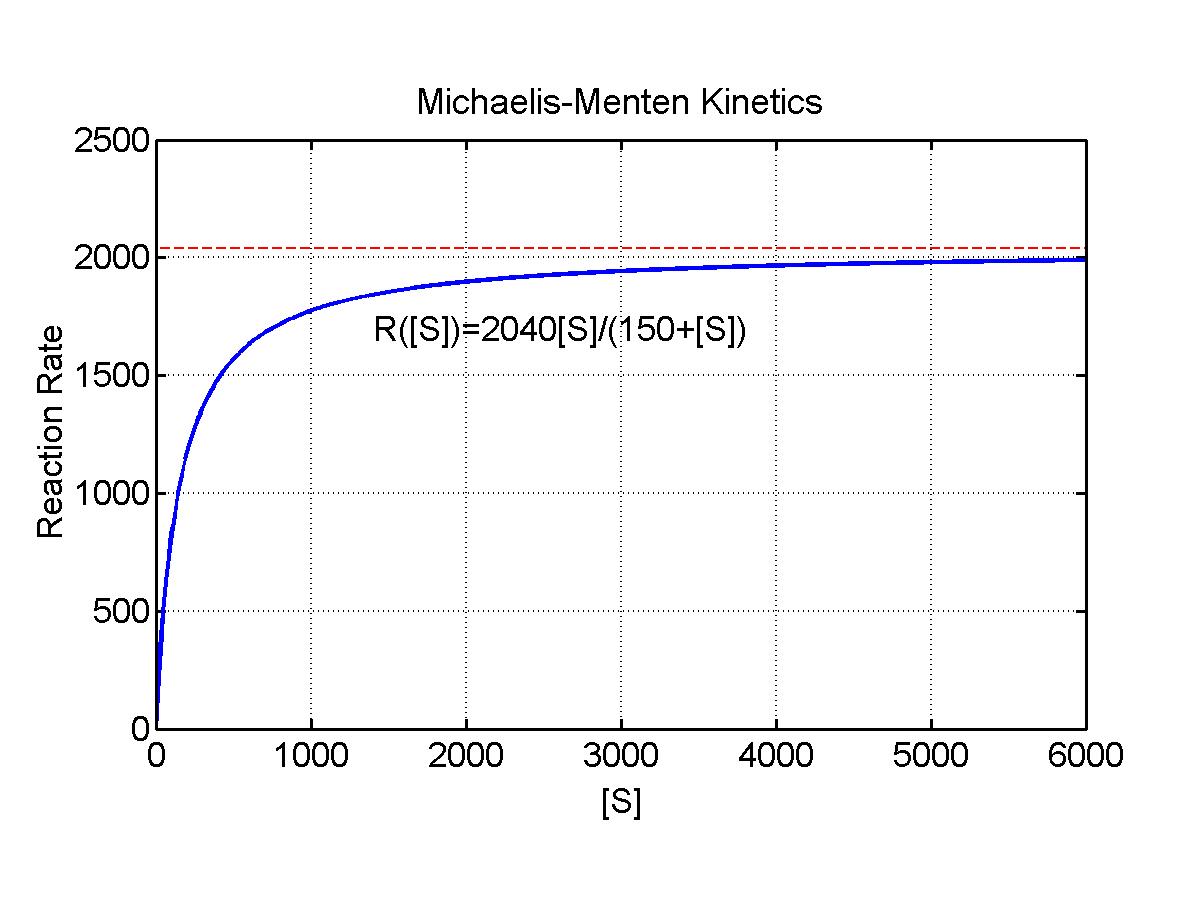
• For rabbit psoas muscle tissue, experimental measurements give V_max = 2040 nm/sec and K_m = 150 mM
• The applet below shows how the reaction rate R varies as a function of [S] = [ATP] for various values of the maximal velocity V and the Michaelis constant K_m
• There is an initial rise in the reaction velocity, which is almost linear
• As the concentration increases, there are diminishing returns with the eventual saturation of the reaction at some maximal rate
• The Worked Examples section shows how a change of variables allows the conversion of this problem into a linear problem, the Lineweaver-Burk plot.

Polynomials and Rational Functions

• The most general polynomial of order n is written:

where the coefficients a_i are constants and n is a positive integer

• Linear functions are first order polynomials
• Quadratic functions are second order polynomials

• Polynomials are used to fit complicated data, providing a simple model
• Excellent routines exist for finding the best least squares fit of a polynomial to data
• Polynomials are defined for all values of x and form very smooth curves
• It easy to use polynomials for interpreting data
  • Finding where minimum and maximum values occur
  • Computing the area under the curve
• These phenomena are topics that Calculus covers

• Polynomials are considered nice functions because of their well-behaved properties
• Difficult to find the roots of an equation (setting p_n(x) = 0) for a polynomial with n > 2, and rarely even possible for n > 4

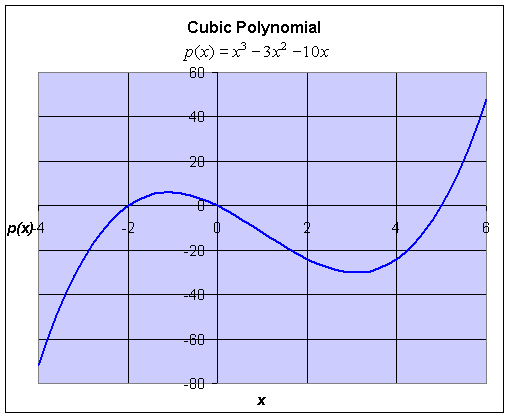
Example: Consider the cubic polynomial given by

Find the roots of this equation and graph this cubic polynomial.

Solution:

• Must find a factorization in order to find the roots of this polynomial (since n > 2).

• The roots of this polynomial are x = 0, -2, or 5
• Later techniques of Calculus will find the high point occurring at (-1.08, 6.04) and the low point occurring at (3.08, -30.04).

Rational functions are the quotient of two polynomials.

• A function r(x) is a rational function if p(x) and q(x) are polynomials and r(x) = p(x)/q(x)
• The domain of the rational function, r(x), is all x such that q(x) does not equal zero
• The roots of the polynomial q(x) are candidates for vertical asymptotes of r(x)
• When the order of the polynomial in the numerator of a rational function is less than or equal to the order of the polynomial of the denominator, then a horizontal asymptote occur
• Commonly occur in biological appications
• For Michaelis- Menten kinetics, the reaction rate satisfies R([S]) as the quotient of the linear functions p([S]) = V[S] and q([S]) = K_m + [S]

Asymptotes: Vertical and horizontal asymptotes are very important for determining the shape of a graph.

Vertical Asymptote: When the graph of a function f(x) approaches a vertical line, x = a, as x approaches a, then that line is called a vertical asymptote.

Horizontal Asymptote: When the graph of a function f(x) approaches a horizontal line, y = c, as x becomes very large (either positve or negative), then that line, y = c, is called a horizontal asymptote.

Let r(x) = p(x)/q(x) be a rational function with polynomials p(x) = a_nxⁿ + ... + a₀ of degree n in the numerator and q(x) = b_mx^m + ... + b₀ of degree m in the demoninator.

1. If n < m, then r(x) has a horizontal asymptote of y = 0.
2. If n > m, then r(x) becomes unbounded for large values of x (positve or negative).
3. If n = m, then r(x) has a horizontal asymptote of y = a_n/b_n.

Example: Let us examine the rational function

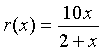
Find the domain of this function, the x and y-intercepts, and vertical and horizontal asymptotes, then sketch a graph of the function.

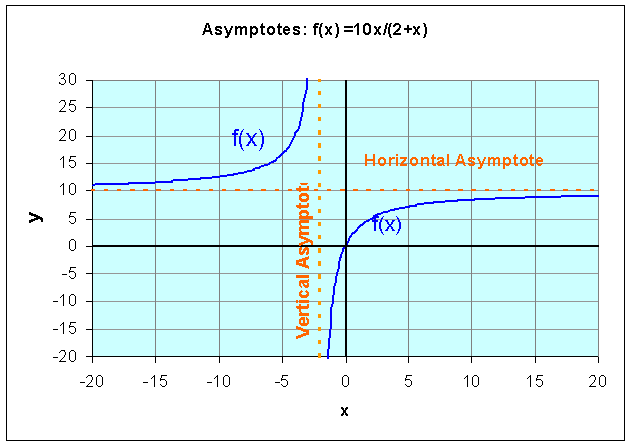
Solution:

• The domain of this function must exclude x = -2
• Since r(0) = 0 and 10x/(2+x) = 0 implies that x = 0, the x and y-intercepts are easily seen to be zero. Thus, this function passes through the origin
• As x gets close to -2, the function becomes undefined and the value of r(x) goes to either positive or negative infinity. Thus, x = -2 becomes a vertical asymptote.
• For large values of x, r(x) approaches 10x/x = 10. This becomes the horizontal asymptote

A hyperlink is provided to Worked Examples to show you how to work with rational functions.

Acid Chemistry Revisited

From before, the concentration of the acid, [H⁺], for a weak acid uses the quadratic formula. The concentration of acid depends on the equilibrium constant and the normality, x, of the weak acid solution.

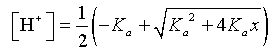
Since the equilibrium constant is fixed depending on the particular weak acid, we see that the [H⁺] is a function of the normality of the solution, x, and it is a square root function.

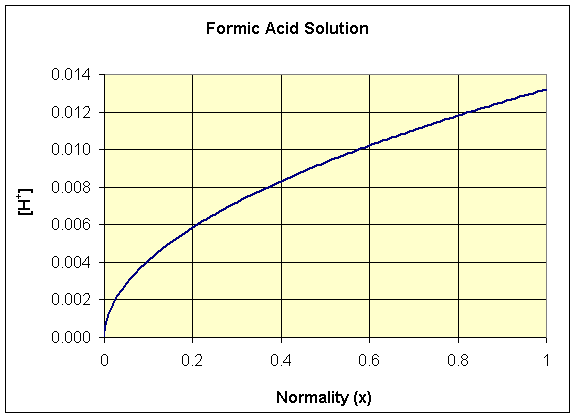
Below is a graph of the [H⁺] as a function of x for formic acid, where K_a = 1.77×10^-4. Note that this function has the shape of a quadratic function rotated 90^o.

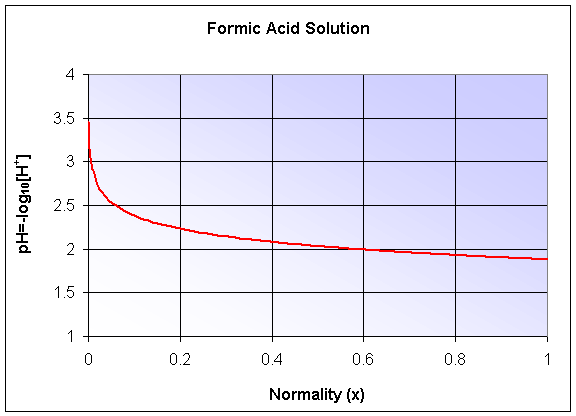
The pH of the solution is -log₁₀([H⁺]), which becomes a composite function. Logarithms are studied in the next section.

Square Root Function

• The square root function is the inverse of the quadratic function
• The square root function is only defined for positive quantities under the radical
• The domain of a square root function is found by solving the inequality for the function under the radical being greater than zero

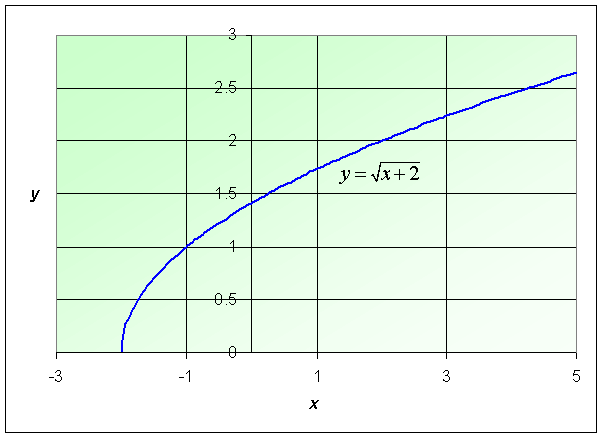
Example: Consider the function

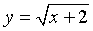
Find the domain of this function and graph the function.

Solution: The domain of this function satisfies x + 2 > 0 or x > -2.

See the Worked Examples section for more information on square root functions.

References:

[1] E. Pate (1997), "Modeling of muscle crossbridge mechanics," in Case studies in Mathematical Modeling - Ecology, Physiology, and Cell Biology, eds. H. G. Othmer, F. R. Adler, M. A. Lewis, and J. C. Dallon, Prentice-Hall.