Math 121 - Calculus for Biology I Spring Semester, 2009 Introduction to the Derivative
	© 2001, All Rights Reserved, SDSU & Joseph M. Mahaffy San Diego State University -- This page last updated 14-Mar-09

1. Introduction to the Derivative
2. Derivative as a Growth Rate
   1. Juvenile Heights
   2. Yeast Population
3. Derivative as a Velocity
   1. Trotting Horse
   2. Falling under Gravity
   3. Falling Ball
4. Worked examples
5. Reference

Introduction to the Derivative

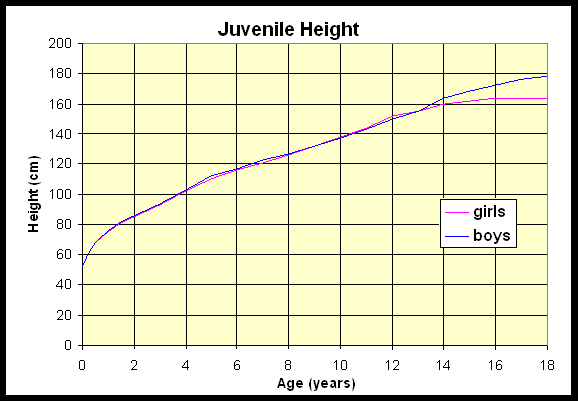
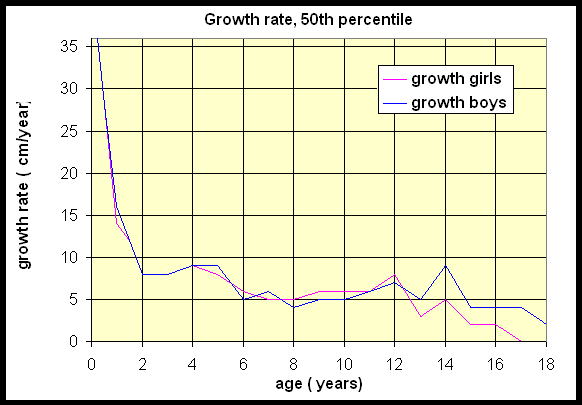
• The derivative is very important  in Calculus
• How to view the derivative
  • Rate of growth
  • Velocity
  • Geometric view:  the tangent line

The Derivative as a Growth Rate

Example 1: Juvenile Heights

• Below is a graph for the heights of girls and boys at the 50^th percentile for ages 0 to 18, introduced in our section on linear functions

 

• The rate of growth is the slope of the line through the data
  • The earliest years show a high rate of growth
  • Over a wide range of ages, the rate of growth is almost constant
  • The later years show the growth rate slowing
• Growth rate is the difference in heights divided by the difference in time measured in years
• The growth rate g(t) is approximated by the formula

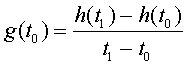
where t₀ and t₁ are successive ages with heights  h(t₀)  and h(t₁)

Examples for girls,

Age (years)	Height (cm)	Annual Growth Rate (cm/yr)
t0 = 2	h(t0) = 87
t1 = 3	h(t1) = 94	g(2) = (h(3) - h(2))/(3 - 2) = 7 cm/yr

Example for boys,

Age (years)	Height (cm)	Annual Growth Rate (cm/yr)
t0 = 3/12 = 0.25 (3 months)	h(t0) = 61
t1 = 6/12 = 0.5 (6 months)	h(t1) = 68	g(0.25) = (h(0.5) - h(0.25))/(0.5-0.25) = 28 cm/yr

• Below is the graph of the growth rates for girls and boys
  • The growth rate is higher for early years
  • Stays almost constant for many years
  • Drops almost to zero in the late teens

 

Example 2: Yeast Population

• Carlson (1913) studied a growing culture of yeast
• Below is a table of the population (in thousands/cc)
   

• A graph of these data is presented below

• This graph exhibits what is classically called an S-shaped curve
  • This shape occurs frequently in biological models

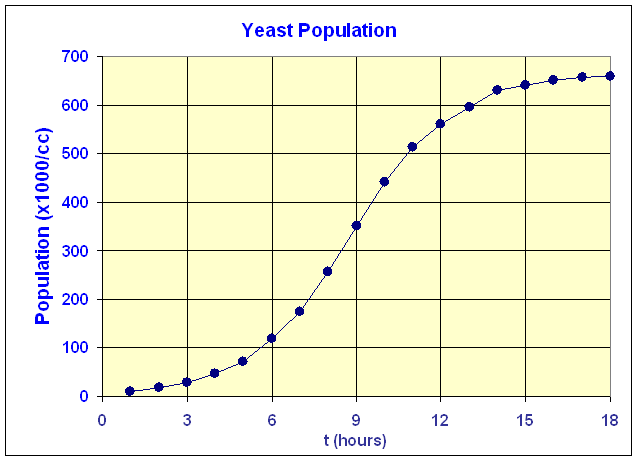
• The growth rate for the population of yeast

  • Slow for early hours of growth
  • Increases to a maximum near 8 hours
  • Decreases and levels off as the population reaches its carrying capacity

   

• Define the population at each hour as P(t)
• The growth of the yeast for each hour is computed

• This is the slope of the curve computed between each of the data points
• The graph of the growth function g(t) is shown below

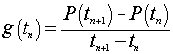
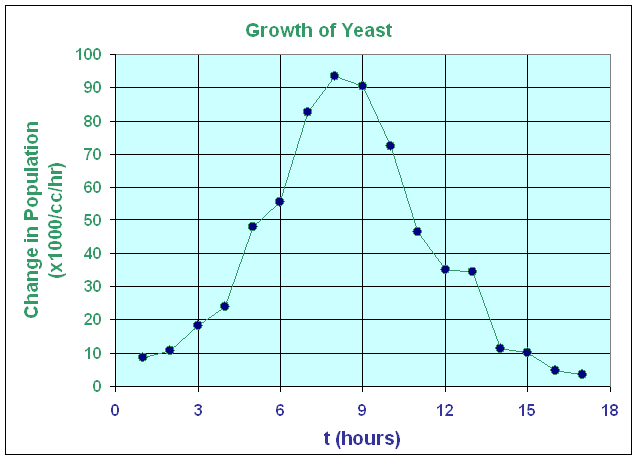
• With more data, we might expect a smoother growth curve

• It is very important to note that the graph of the yeast population (above) and the graph of the growth of the yeast population (below) are different graphs, but are related through the slope of the population graph

• The derivative will be the instantaneous growth rate at any time for any population curve

The Derivative as a Velocity

Example 3:Trotting Horse

• In the 1800s, controversy whether or not a trotting horse ever had all feet off of the ground
• Eadweard Muybridge developed special photographic techniques for viewing animals and humans in motion
• Timed sequences of still pictures, precursor to modern motion pictures

Study of a trotting horse

• What is the velocity of the trotting horse?
• How fast is a particular animal or what speed is a bird flying?
  • How would you find the speed of a cheetah hunting a Thompson's gazelle?
  • Or the velocity of a peregrine falcon diving to catch a pigeon?

 

Image 1, time = 0 sec	Image 2, time = 0.04sec	Image 3, t = 0.08 sec	Image 4, t = 0.12 sec	Image 5, t = 0.16 sec
Image 6, t = 0.2 sec	Image 7, t = 0.24sec	Image 8, t = 0.28 sec	Image 9, t = 0.32 sec	Image 10, t = 0.36 sec

 

Velocity

• Find the velocity of the trotting horse
• Velocity has units of distance divided by time
  • Compute the distance covered between successive picture frames
  • Divide by the time between the pictures
• Scale in the background measures the distance (in feet)
• The time between frames is 0.04 seconds
• Using the man's head for a reference point
  • The position at t₀ = 0 is s(t₀) = 3.5 ft
  • At t₁ = 0.04, the head is at s(t₁) = 4.5 ft
  • The velocity is

• At t₂ = 0.08, the head is at s(t₂) = 5.6 ft, so the velocity satisfies

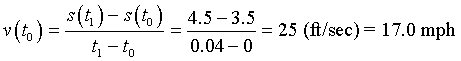
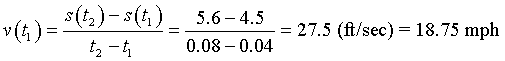
which is approximately the same

• An average velocity for the entire sequence is computed by taking the initial and final positions of the head and dividing by the total time between the frames

• So we see that the velocity is relatively constant over the short time interval of the pictures

• What if we asked for the velocity of the right front hoof?
• This sequence of pictures is inadequate
• Does the right front hoof stop or move backwards at any time?
• How would you answer this question?

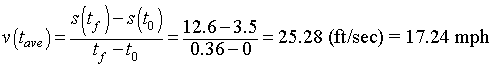
Example 4: Falling under the influence of Gravity

• The classical study for velocity is the motion of a falling ball
• University of British Columbia website simulates a strobe light to capture the motion of a ball
• Consider gravity applied to the animated cartoon of Wile E. Coyote
• What resolution is needed to visualize the effects of gravity?
• Below is Wile E. Coyote falling off a cliff that is about 500 feet high

If we look once every 10 seconds, we see 

Consider 5 second intervals instead

Now consider 1 second intervals of time.

• This animation gives a better sense of Wile E. Coyote's fall
• We see that the distance travelled each second is longer
• This resolution shows the changing velocity

Example 5: Falling Ball

• Below is an applet that simulates a ball falling under gravity (no air resistance)
• A strobe light catches the position of the ball at regular time intervals
• The applet allows different intervals of time between the flashes of the strobe light

Change the time between strobe flashes by entering different values in the window. The left frame shows the position of the ball as it drops, while the right frame graphs the position as a function of time.

Alternate link

• The next section examines the geometric perspective of the derivative as a tangent line
• The formulae above are similar to the equations for the slope of a line
• Our geometric viewpoint of a derivative will be equivalent

Worked Examples

References

[1] T. Carlson Über Geschwindigkeit und Grösse der Hefevermehrung in Würze. Biochem. Z. 57: 313-334, 1913.