Math 121 - Calculus for Biology I Spring Semester, 2004 Applications of the Derivative
	© 2001, All Rights Reserved, SDSU & Joseph M. Mahaffy San Diego State University -- This page last updated 01-Jan-04

1. Temperature Fluctuation during Menstrual Cycle
2. Maxima, Minima, and Critical Points
3. Graphing Polynomials
4. Second Derivative and Concavity
5. Points of Inflection
6. Worked Examples

Applications of the Derivative

1. Finding Maxima, Minima, and Steepest parts of a Function
2. Classical Calculus application - Sketching the graph of a function

Body Temperature Fluctuation during the Menstrual Cycle

• Mammals regulate their body temperature in a narrow range to maintain optimal physiological responses
• Variations in body temperature occur during exercise, stress, infection, and other normal situations
• Neurological control of the temperature
• Variations include
  • Circadian rhythms (a few tenths of a degree Celsius)
  • Menstrual cycle - Ovulation often corresponds to the sharpest rise in temperature

• Graph of the basal body temperature taken at the same time each day for a one 28-day period of one woman
• The data are fit by a cubic polynomial

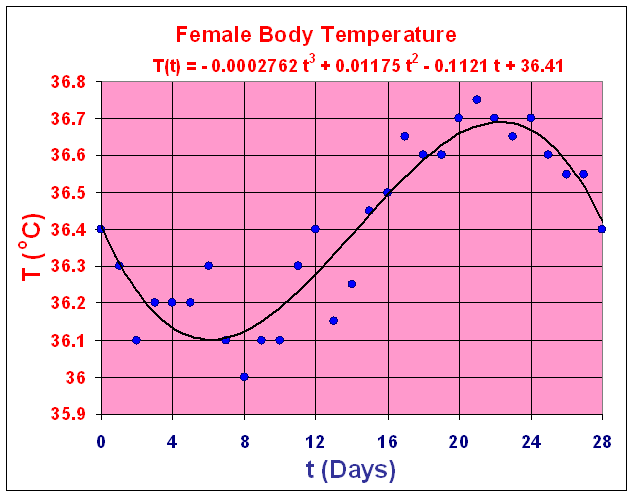
• The best cubic polynomial fitting the data above is

T(t) = -0.0002762 t³ + 0.01175 t² - 0.1121 t + 36.41

• Want to find the high and low temperatures
• Determine the time of peak fertility when the temperature is rising most rapidly

Maxima and Minima

• The high and low temperatures occur when the curve has slope of zero
• Find the derivative equal to zero
• The derivative of the temperature is

T '(t) = -0.0008286 t² + 0.02350 t - 0.1121

• Note that the derivative is a different function from the original function

• The roots of the derivative (quadratic equation) are

t = 6.069 and 22.29 days.

• Thus

Minimum at t = 6.069 with T(6.069) = 36.1 ^oC

Maximum at t = 22.29 with T(22.29) = 36.7 ^oC

• There is only a 0.6 ^oC difference between the high and low basal body temperature during a 28 day menstrual cycle by the approximating function
• The data varied by 0.75 ^oC.

Maximum Increase in Temperature

• The maximum increase in temperature is when the derivative is at a maximum
• This is the vertex of the quadratic function, T '(t)
• The maximum occurs at the midpoint between the roots of the quadratic equation
• Alternately, the derivative of T '(t) or the second derivative of T(t) equal to zero gives the maximum
• The second derivative is

T "(t) = -0.0016572 t + 0.02350

• The second derivative is zero at the

Point of Inflection at t = 14.18 with T(14.18) = 36.4 ^oC.

• The maximum rate of change in body temperature is

T '(14.18) = 0.054 ^oC/day.

• This model suggests that the peak fertility occurs on day 14, which is consistent with what is known about ovulation

Worked Examples

Maxima, Minima, and Critical Points

• The derivative is zero at critical points for the graph of a smooth function

Definition: A smooth function f(x) is said to be increasing on an interval (a,b) if f '(x) > 0 for all x in the interval (a,b). Similarly, a smooth function f(x) is said to be decreasing on an interval (a,b) if f '(x) < 0 for all x in the interval (a,b).

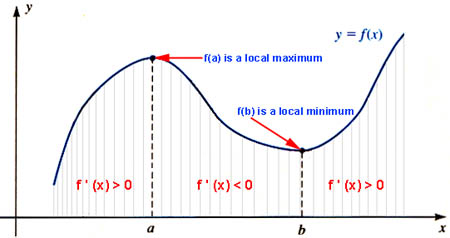
• A high point of the graph is where f(x) changes from increasing to decreasing
• A low point on a graph is where f(x) changes from decreasing to increasing
• In either case the derivative passes through zero

Definition: A smooth function f(x) is said to have a local maximum at a point c, if f '(c) = 0 and f '(x) changes from positive to negative for values of x near c. Similarly, a smooth function f(x) is said to have a local minimum at a point c, if f '(c) = 0 and f '(x) changes from negative to positive for values of x near c.

Definition: If f(x) is a smooth function with f '(x_c) = 0, then x_c is said to be a critical point of f(x).

• Critical points help find the local high and low points on a graph, but some critical points are neither maxima or minima

Graphing Polynomials

Example: Consider

f(x) = x³ - 6x² - 15x + 2

Sketch a graph of f(x).

Solution:

• The derivative

f '(x) = 3x² - 12x - 15 = 3(x + 1)(x - 5)

• The derivative is zero when x_c = -1 or 5
• Since f(-1) = 10, a local maximum occurs at (-1,10)
• Since f(5) = -98, a local minimum occurs at (5,-98)
• The y-intercept is (0,2)

This gives enough for a reasonable sketch of the graph. Note that since this is a cubic equation, the x-intercepts are very hard to find.

 

The Second Derivative and Concavity

• Since the derivative is itself a function, then if it is differentiable, one can take its derivative to find the second derivative often denoted f ''(x)
• If the first derivative is increasing or the second derivative is positive, then the original function is said to be concave upward
• If the first derivative is decreasing or the second derivative is negative, then the original function is said to be concave downward
• The second derivative is a measure of the concavity of a function
• For smooth functions, the maxima generally occur where the function is concave downward, while minima occur where the function is concave upward

The Second Derivative Test. Let f (x) be a smooth function. Suppose that f '(x_c) = 0, so x_c is a critical point of f. If f ''(x_c) < 0, then x_c is a relative maximum. If f ''(x_c) > 0, then x_c is a relative minimum.

Example: For

f(x) = x³ - 6x² - 15x + 2

• The second derivative is

• The critical points occurred at

x_c = -1 and 5

• The second derivative at the critical point x_c = -1 gives

f ''(-1) = -18

• The function is concave downward at -1, so this is a relative maximum
• The second derivative at the critical point x_c = 5 is

f ''(5) = 18

• The function is concave upward, so this is a relative minimum.

Points of Inflection

• When the second derivative is zero, then the function is usually changing from concave upward to concave downward or visa versa
• This is known as a point of inflection
• A point of inflection is where the derivative function has a maximum or minimum, so the function is increasing or decreasing most rapidly
• From an applications point of view, if the function is describing a population, then the point of inflection would be where the population is increasing or decreasing most rapidly
• The point of inflection measures when the change of a function is its greatest or smallest.

• From a graphing perspective, the point of inflection shows the visual change in concavity
• It is not nearly as important as extrema, but does provide one more point to aid in graphing the function

Example: For

f(x) = x³ - 6x² - 15x + 2

The second derivative is

f ''(x) = 6x - 12

The point of inflection is f ''(x) = 0 which is when x = 2

The point of inflection occurs at (2, -44)

Worked Examples