|
|
Math 121 - Calculus for Biology I |
|
|---|---|---|
|
|
San Diego State University -- This page last updated 09-Feb-09 |
|
Allometric Modeling
|
|
Math 121 - Calculus for Biology I |
|
|---|---|---|
|
|
San Diego State University -- This page last updated 09-Feb-09 |
|
Allometric Modeling
Cumulative AIDS cases
The advent of AIDS in modern society has had a significant impact on both personal behavior and public policy. The new protease inhibitors have significantly improved the quality of life for those who are HIV positive; however, this has come at a substantial cost to society. The new drugs are extremely expensive, are difficult to take because of the complex scheduling requirements to be effective, and have many strong side effects (besides not always working for a particular person or strain of the HIV virus). In turn, there are a number of people who are now avoiding safe sex practices as they no longer fear the "Death Sentence" that used to be associated with an HIV infection. Below is a figure illustrating the HIV virus. It has links to more images with more details about the virus.
|
......
|
||
|
..
|
.. |
|
|
[click
for enlarged and detailed image] |
There is an important need for our society to know the extent of this disease from both an economic and sociological perspective. In order to make informed public policy, we need to know what is the expected case load in the upcoming years. However, it is clearly an extremely complex modeling problem. Below is a table of cumulative cases of AIDS between 1981 and 1992 [1] and an animated .gif showing the spread of the disease (through mortality statistics) over a similar period of time.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
..
|
|
.. |
A quick glance at the data will clearly show that it is not linear, so a linear model is not appropriate. There are general methods for finding the least squares best fit to nonlinear data. However, these techniques are very complicated an often difficult to implement. A hyperlink provides an applet for finding the best nonlinear least squares fit to the data for cumulative AIDS cases, which is different from the technique we'll show below.
As noted above, using a least squares fit to nonlinear data can be extremely difficult. However, there are a few standard nonlinear models used in biological applications that are more easily analyzed. The technique that we'll develop in this section is known as the Power Law of Modeling. It is also referred to as Allometric Modeling. Allometric models are used regularly in modeling complex biological phenomena where the actual mechanisms underlying the model behavior are too complex to describe in detail, but there is a need to be able to make some predictions.
Allometric models assume a relationship between two sets of data, x and y, that satisfy a power law of the form
where A and r are parameters that are chosen to best fit the data in some sense. Note that this model assumes that when x = 0, then y = 0. As always, you should be aware of the limitations of this type of modeling. This method provides its best predictive capabilities when examining a situation that lies between the given data points. For example, if the number of species of herptofauna on Carribean islands is determined for a collection of islands with varying areas, then this model would give a reasonable estimate for the expected number of species on another Carribean island with an area that lies between the collected data. It would not be appropriate for extending to a large continent as the area is significantly beyond the range of the collected data.(This example is covered in a Lab exercise.) It wouldn't even be appropriate for another island such as Iceland, which lies in a different type of climate and has a different geography.
Allometric models are found by taking the logarithms of the data (or graphing the data on log-log graphs) and seeing if the data lie roughly on a straight line. If this is the case, then a power law relationship makes a reasonable model. Below is an applet showing the linear least squares fit to the logarithms of the data for cumulative aids cases, and the graph to the right shows the modeling relationship with a normal scale. The allometric model has x be time in years since 1980 and y be the cumulative AIDS cases.
The applet above can be adjusted until you reach a minimum least squares for the log of the data with J(A,r) = 0.10. The best slope is r = 3.27 and the best intercept is ln(A) = 4.42. We will show later that this gives the best fit power law for this model as
The graph shows that the power law provides a reasonable fit to the data. Unfortunately, the fit is weakest at the end where we'd like to use the model to predict the cumulative AIDS cases for the next year. The model predicts 366,990 cases in 1993, which is clearly too high from the given data. However, the analysis does give some indication of the rate of growth for this disease, which provides a first approximation for improved models and could be applied to expected spread of another disease with similar infectivity as HIV. This modeling technique is still valuable for analysis of many other data sets and occasionally can provide insight into the underlying biology of the problem. A better fit to the data is shown in the nonlinear least squares appendix that can be viewed through the hyperlink.We will see more examples of this in the computer labs.
Our least squares best fit to the data above uses the logarithms of the data. To detail how the parameters A and r in the model are found, we need to review the properties of exponents and logarithms.
Review of Exponents and Logarithms
There are several properties of exponents that you should remember from algebra.

These properties can be used to simplify expressions involving exponents.
To solve equations that have exponents in them, we need to have the inverse function of the exponent. This is the logarithm. If you are given the equation,
then the inverse equation that solves for x is given by
The a in the above expression is called the base of the logarithm. Again there are a collection of properties of logarithms that prove useful for solving equations and simplifying expressions.
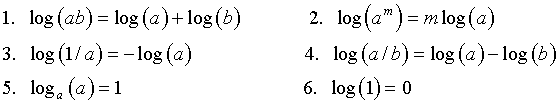
Note that in the properties of logarithms, we only needed to specify the base of the logarithm for Property 5. All other properties are independent of which base is used. The two most common logarithms that are used are log10 and loge. The latter logarithm is called the natural logarithm, often denoted log or ln, and is the one most commonly used (and is the default on your calculator). Later you will learn about the importance of the natural base e. For most of our work, we will use the natural logarithm. (Note that Excel defaults to log10.)
Graphing Exponentials and Logarithms
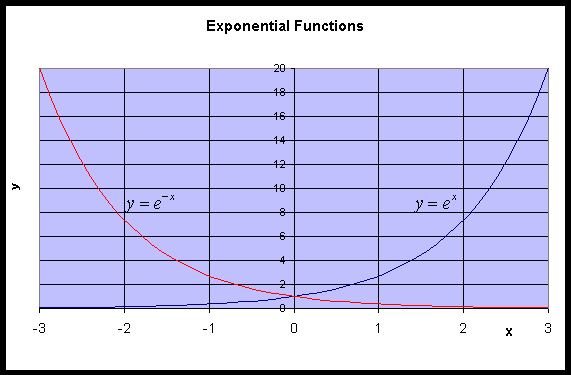
As noted above, the exponential function, ex, and the natural logarithm, ln(x), are inverse functions of each other. In this section we show the graphs of these functions to develop some sense of their behavior. We will study ex in greater detail after learning more about the derivative. However, for graphing purposes you need to know that e is an irrational number between 2 and 3, more precisely, e = 2.71828.... The domain of ex is all of x becoming extremely small very fast for x < 0 (a horizontal asymptote of y = 0) and growing very fast for x > 0. Its range is y > 0. Similarly, the graph of y = e-x has the same y-intercept of 1, but its the mirror reflection through the y-axis of y = ex. It becomes very large for x < 0 and very small for x > 0. A graph of both y = ex and y = e-x is given below.
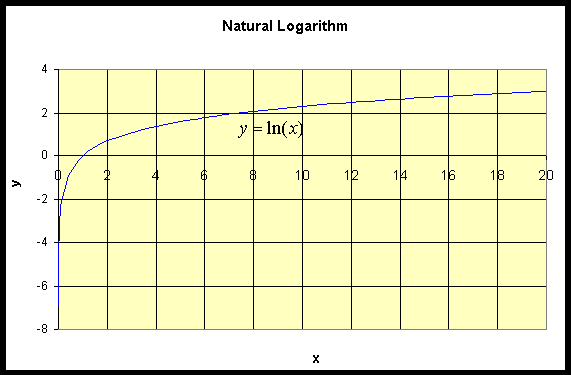
Since ln(x) is the inverse function of ex, an easy way to graph this function is to mirror the graph of ex through the line y = x. The domain of ln(x) is x > 0, while its range is all values of y. As y = ln(x) becomes undefined at x = 0, there is a vertical asymptote at x = 0. The graph of y = ln(x) is given below.
We will see that the exponential function plays a role in many applications, so it is very important to understand this function and how its graph behaves. Several examples are illustrated in the hyperlinked Worked Examples for Exponentials and Logarithms section.
We return to the Allometric model developed above, where two sets of data, x and y are assumed to satisfy a power law of the form
We want to choose the parameters A and r that best fit the data. The next step is to take the logarithm of both sides, then use the properties of logarithms to simplify the equation.
From this formula, we see that if we take the logarithm of the data, ln(x) and ln(y) and graph it we should see a straight line. That is, if we take X = ln(x), Y = ln(y), and a = ln(A), then the above equation can be written Y = a + rX , which is a line with a slope of r and a Y-intercept of ln(A).
We return to the example at the beginning of this section. Below is a table that includes both the data and the logarithms of the data.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Below shows a graph of the logs of the data (year-1980 and cumulative AIDS cases) along with the best straight line fit.
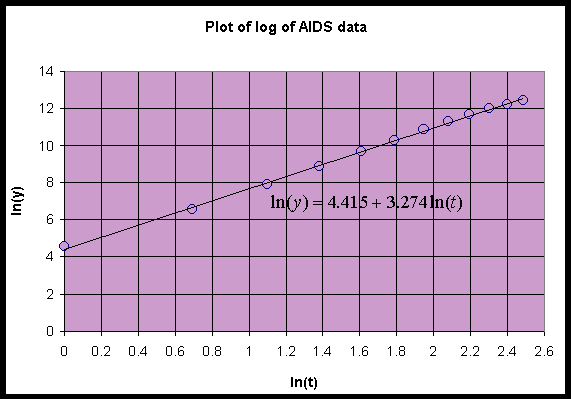
The plot above shows that when the logarithms of the data for the cumulative AIDS cases are plotted against the logarithms of the time since 1980, then these logarithmic data lie fairly close to a straight line though the data are flattening for the later years suggesting a diminished rate of increase. The least squares best fit of the straight line to the logarithms of the data give a slope of r = 3.274 and intercept of a = ln(A) = 4.415, which gives A = 82.70. Whenever this is the case, then an allometric or power law model makes a reasonable description of the data.
There exist graphing routines that readily create what is known as a log-log plot. This allows the user to simply graph the data directly onto a graph with logarithmic scales on the axes to see if the data falls on a straight line suggesting an allometric or power law model. Below we show a plot of the original data on cumulative AIDS cases against the date - 1980 on a graph with logarithmic scaled axes.
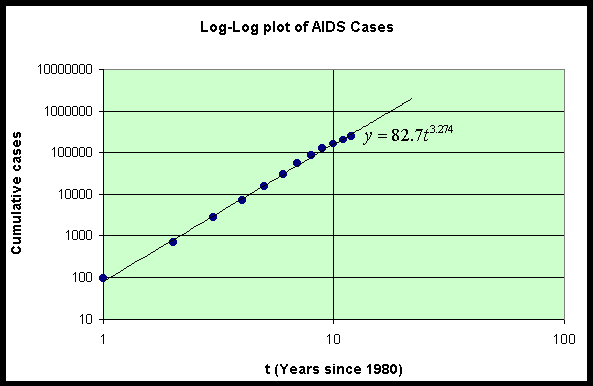
Our work above shows that allometric modeling is essentially finding the best straight line through the logarithm of data. Below is an example, where it is assumed that the model fits an allometric model. By finding the straight line through the logarithms of the two data points, the model is formulated and can be applied to other cases.
Example: (Weight and pulse) We know that smaller animals have a higher pulse than larger animals. Let us assume that this relationship satisfies an allometric model. Later in Lab we will perform a more detailed study of this phenomenon to check on the validity of using the allometric model (or power law).
We are given that a 17 g (or .017 kg) mouse has a pulse of 500 beats/min. Assume a 68 kg human has a pulse of 65. Use these data to form an allometric model and predict the pulse for a 1.34 kg rabbit.
Solution: The power law gives
Next we take logarithms to obtain:
As noted above, this is a straight line in ln(P) and ln(w) with slope of k and intercept of ln(A). From the data,
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
The slope k is given by:
![]()
We can use this slope with one of the points to find ln(A) as follows:
Thus,
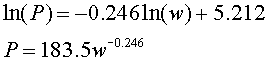
If we use the first equation with a 1.34 kg rabbit, then it gives P = 171.
[1] E. K. Yeargers, R. W. Shonkwiler, and J. V. Herod, 1996, An Introduction to the Mathematics of Biology: with Computer Algebra Models, Birkhäser, Boston.