Math 121 - Calculus for Biology I Fall Semester, 2003 Allometric Modeling - Worked Examples
	© 1999, All Rights Reserved, SDSU & Joseph M. Mahaffy San Diego State University -- This page last updated 06-Jan-03

 
1. Exponential and Logarithm Functions
2. Graphing Exponential and Log Functions
3. Allometric Models

Below are a collection of worked examples that use the exponential function, e, and the natural logarithm, ln. Also, there is a word problem on biodiversity to show an application to allometric modeling.

Examples of Exponential and Logarithmic Functions

Example 1: Solve the equation

e^x-2 = 3.

Solution:

Taking the natural logarithm of both sides gives

so

Example 2: Solve the equation

ln(2x + 1) = 4.

Solution:

Exponentiating both sides, we find

so

Graphing Exponential and Log Functions

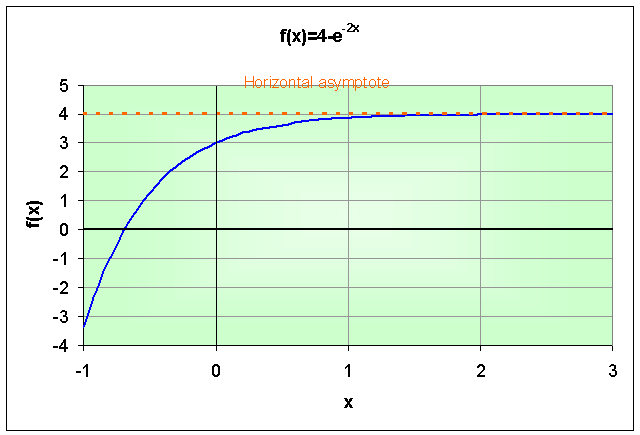
Example 3: Graph the equation

f(x) = 4 - e^-2x.

Determine all intercepts and any horizontal asymptotes.

Solution:

We begin by finding the intercepts. When x = 0, f(0) = 4 - e⁰ = 4 - 1 = 3.

Thus, the y-intercept is (0,3).

Solving 4 - e^-2x = 0, gives e^-2x = 4 or e^2x = 1/4.

Thus, 2x = ln(1/4) = ln(2^-2) = -2ln(2) or x = -ln(2) = -0.6931.

Therefore, the x-intercept is (-0.693,0).

For large values of x, e^-2x is very close to zero, so there is a horizontal asymptote for large positive x with f(x) tending toward 4.

The graph is shown below.

Example 4: Graph the equation

f(x) = ln(x + 2).

Determine all intercepts and any vertical asymptotes.

Solution:

The domain of f(x) is x > -2. We begin by finding the intercepts. When x = 0, f(0) = ln(2) = 0.6931. Thus, the y-intercept is (0,0.693).

Solving ln(x + 2) = 0, gives x + 2 = 1 or x = -1. Thus, the x-intercept is (-1, 0).

There is a vertical asymptote at the edge of the domain, where x = -2.

The graph is shown below.

Allometric Modeling

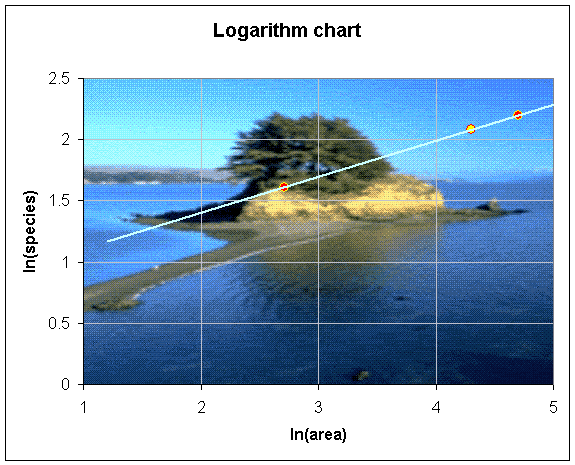
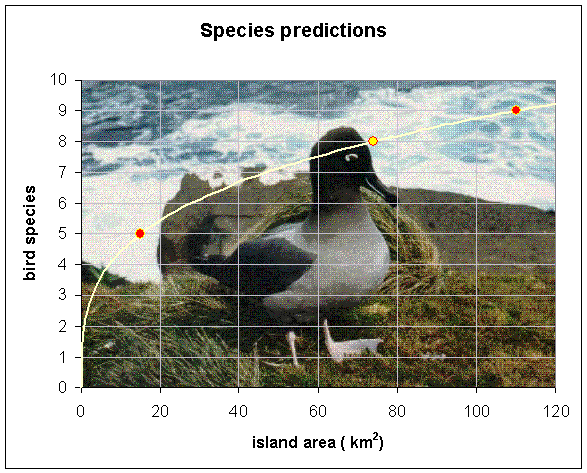
Example 5: There are three Pacific islands in a chain. Island A is 15 km², Island B is 110 km², and Island C is 74 km². An extensive biological survey finds 5 species of birds on Island A and 9 species of birds on Island B.

a. Assume a power law relationship between the number of species (N ) on each of these islands and their area (A) of the form

N = kA^x.

Use the data from Islands A and B to determine the constants k and ^x. Use this expression to predict the number of species on Island C.

b. How large of an island would be required to support 20 species of birds near this chain of islands?

Solution:

a. Taking the natural logarithm of both sides of the given power law relationship and then solving for slope x, we obtain

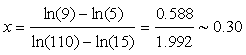
We can use this slope with either of the points (A, N) to find ln(k)

ln(5) = ln(k) + 0.30 ln(15)

ln(k) = ln(5) - 0.30 ln(15) = .797

k ~2.2

So the power law relationship is given by

N = 2.2 A^0.30

We can now predict the number of species on Island C

N = 2.2(74)^0.30 = 8

Thus, there should be 8 species on Island C. Below is a graph showing the data, model, and prediction.

b. We can use this model to predict the size of an island necessary to support 20 species as follows:

20 = 2.2A^0.30

Solving for A,

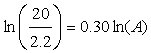
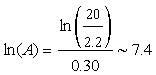
Exponentiating both sides, we find the island area A = 1636 km².

Below is a graph of the logarithms of the data and the straight line fit that the allometric model gives.