1. Introduction
2. Malthusian Growth
3. Solution to the Malthusian Growth Model
4. Radioactive Decay
5. Problems

Introduction

Differential equations frequently arise in modeling situations.They can describe population growth, chemical reactions, heat exchange, motion, and many other applications. The previous sections have considered discrete dynamical systems, especially related to growth. Differential equations can be thought of as a continuous extension of the discrete dynamical systems.

A differential equation is any equation of some unknown function that involves some derivative of the unknown function. The classical example that first gave rise to differential Calculus is Newton's Law of motion. According to Newton's Law of motion, the mass of an object times its acceleration is equal to the sum of the forces acting on that object. However, acceleration is simply the first derivative of velocity or the second derivative of position. So Newton's Law of motion is an example of a differential equation. In biology, there are many applications of differential equations. Most frequently, a differential equation is describing either a growth rate or a reaction rate.

Malthusian Growth

The first model we studied in discrete dynamical systems was the discrete Malthusian growth model. Recall that this model could be written

where P_n is the population at time n and r is the rate of growth. This equation can be rearranged to give

which says that the change in population between the (n + 1)^st time period and the n^th time period is proportional to the population at the n^th time period.

Now we want to write this model in terms of continuous time variables. Define P(t) to be the population at any time t. Assume that r is the rate of change of the population per unit time per animal in the population. If we let Dt be a small interval of time, then the change in population between t and t + Dt, satisfies the equation

Biologically, this equation says that the change (difference) in the population over a small period of time is found by taking the rate of growth times the population times the interval of time Dt. The equation above can be rearranged to give

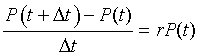
The right hand side of the equation readily transforms into a derivative as we take the limit of Dt tending toward zero. Thus, in the limit this model reduces to the differential equation

This is the continuous Malthusian growth model.

Solution to the Malthusian Growth Model

The differential equation describing the continuous Malthusian growth model says that the derivative of an unknown Population function P(t) is equal to a constant times the unknown Population function. (The rate of change of a population is proportional to the population.) The only function that we know that is a derivative of itself is the exponential function. We try a solution of the form

where c is an arbitrary constant. But P'(t) is cre^rt, which is rP(t), so satisfies the differential equation. If we add an initial condition P(0) = P₀, then the unique solution becomes

This is another reason why Malthusian growth is often called exponential growth.

Example 1: Consider the Malthusian growth model

Find the solution and determine how long it takes for this population to double.

Solution: From above we see that the solution is given by

This population doubles when 200 = 100e^0.02t . Thus, 0.02 t = ln(2) or t = 50 ln(2) = 34.66.

Example 2: Suppose that a culture of Escherichia coli is growing according to the Malthusian growth model

If the population doubles in 30 minutes, then find the value of r.

Solution: From above we see that the solution is given by

This population doubles when 2P₀ = P₀ e^30r. Thus, e^30r = 2 or 30r = ln(2) or r = ln(2)/30 = 0.0231 min^-1.

Radioactive Decay

Radioactive elements play an important role in many biological applications. Many experiments use radioactive tracers to determine what sequence of molecular events occurred. For example, ³H (tritium) can be used to tag certain DNA base pairs, which can then be added to mutant strains of E. coli that are unable to manufacture one particular DNA base. By treating the culture with the appropriate antibiotics, one can use the radioactive signal to determine how much DNA was replicated under a particular set of experimental conditions. Radioactive iodine is often used to detect thyroid problems in humans. In most cases, the experiments are run in such a way that radioactive decay is not an issue. (³H has a half-life of 12.5 yrs or ¹²⁵I has a half-life of 56 days.)

One important application of radioactive decay is the dating of biological specimens. While an organism is living, it is continually changing its carbon with the environment. (Plants directly absorb CO₂ from the atmosphere, while animals get their carbon either directly or indirectly from plants.) Gamma radiation that bombards the Earth keeps the ratio of ¹⁴C to ¹²C fairly constant in the atmospheric CO₂. The ¹⁴C that entered a living organism can be used to determine how much time has passed since it has died. It has been determined that radioactive carbon, ¹⁴C, decays with a half-life of 5730 years, i.e., in 5730 years the quantity of ¹⁴C decreases to half its original amount. Living tissue shows a radioactivity of about 15.3 disintegrations per minute (dpm) per gram of carbon, which means that 5730 years after the organism has died, it will exhibit only half or 7.65 dpm per gram of carbon.

Let R(t) represent the number of dpm per gram of carbon from an ancient object. The loss of ¹⁴C from a sample at any time t is proportional to the amount of ¹⁴C remaining. Thus, the amount of ¹⁴C is directly related to R(t) which satisfies the differential equation

From our solution for the Malthusian growth model, it is clear that this differential equation has the solution, R(t) = 15.3e^-kt, where k = ln(2)/5730 = 0.000121.

Example 3: Suppose that an object is found to have a radioactive count of 5.2 dpm per g of carbon. Find the age of this object.

From the solution above

Thus, t = ln(2.94)/k = 8915 yr., so the object is about 9000 yrs old.

Problems:

 1. A population of bacteria begins with 1,000,000. The population is growing according to the Malthusian growth equation given by

where t is in minutes. Find how long it takes for this population to double. Find the population after one hour.

2.a. A population of yeast satisfies the differential equation for Malthusian growth.

If this population satisfies

with an initial population of 100 and t in hours, then determine its population as a function of time, and find at what time the population doubles.

b. A competing population is falling, due to the presence of this new population. Suppose it satisfies the initial value problem

Find the solution to this problem, and determine when its population is half of its original population.

c. Find when the two populations are equal.

3. a. The population of Canada 1 was 24,070,000 in 1980, while in 1990 it was 26,620,000.  Assuming the population is growing according to the principle of Malthusian growth (with no food or space limitations), find the population as a function of time, and determine its doubling time.

b. For the same years, the populations of Kenya were 16,681,000  and  24,229,000 respectively. Find the population as a function of time.

c. In what year do the populations of Canada and Kenya  become equal?

4.  A radioactive substance satisfies the differential equation

for some constant k.

Suppose that initially there are 10gm of the substance. After 25 days there are 8gm remaining. Find k and determine the half-life of the substance(time when R(t) =5 )

5.  When Strontium-90 (⁹⁰Sr) is ingested, it can displace calcium in the formation of bones. After a beta decay it becomes an isotope of krypton (an inert gas), and diffuses out of the bone, leaving the bones porous.

a. Suppose that a particular bone contains 20 grams of ⁹⁰Sr, which has a half-life of 28 years. Write an equation describing the amount of ⁹⁰Sr remaining at any time, and determine the amount after 10 years.

b. Find how long until only 7 grams of ⁹⁰Sr remain.