Math 121 - Calculus for Biology I Fall Semester, 2003 Applications of the Derivative
	© 2001, All Rights Reserved, SDSU & Joseph M. Mahaffy San Diego State University -- This page last updated 07-Jan-03

1. Stability of the Logistic Growth Model
2. Behavior of the Discrete Dynamical Model
3. Height of the Ball Revisited
4. Maxima, Minima, and Critical Points
5. Graphing Polynomials
6. Second Derivative and Concavity
7. Points of Inflection
8. Worked Examples

This section examines applications of the derivative to problems that we have worked on earlier in the semester. The first part uses the derivative to analyze the stability of discrete dynamical systems. The second part is the more classical Calculus applications, where the derivative is used to help with sketching the graph of a function.

Stability of the Logistic Growth Model

When studying the growth of a culture of yeast, we found that the discrete logistic growth model

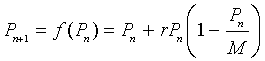
simulated the data quite well. However, the applet for the discrete logistic growth model showed that the behavior of this model changes very dramatically as the parameter r varies. The derivative of the function f(P) is a valuable tool for determining the behavior of the discrete dynamical system near an equilibrium point.

The discrete logistic growth model, as given by the equation above, has two equilibria,

It is easy to see that the derivative of f(P) is given by

At P_e = 0, the derivative satisfies

which for r positive always results in solutions growing away from this equilibrium. (If r is a negative number between -1 and 0, then the solution of the discrete logistic growth model decays to 0 or the population goes to extinction.)

The more interesting behavior occurs around the second equilibrium, P_e = M. Below is a summary of the types of behavior that are observed for a discrete dynamical system near an equilibrium, P_e. (In all of the descriptions below, we are assuming that the simulation begins "near" the equilibrium value.

Behavior of the Discrete Dynamical Model near an Equilibrium

1. If f '(P_e) > 1, then the solutions of the discrete dynamical model grow away from the equilibrium (monotonically). Thus, the equilibrium is unstable.
2. If 0 < f '(P_e) < 1, then the solutions of the discrete dynamical model approach the equilibrium (monotonically). Thus, the equilibrium is stable.
3. If -1 < f '(P_e) < 0, then the solutions of the discrete dynamical model oscillate about the equilibrium and again the equilibrium is stable.
4. If f '(P_e) < -1, then the solutions of the discrete dynamical model oscillate but move away from the equilibrium. Again, the equilibrium is unstable.

Returning to the logistic growth model, we can evaluate the derivative at the larger equilibrium, P_e = M. From the formula for the derivative, it is easy to see that

From our list of behaviors above, it is follows that

1. If 0 < r < 1, then the solution of the discrete logistic model monotonically approaches the equilibrium, P_e = M, which was the case observed for the experiment with the yeast.
2. If 1 < r < 2, then the solution of the discrete logistic model oscillates about the equilibrium, P_e = M, but the solution still asymptotically approaches this equilibrium.
3. If 2 < r < 3, then the solution of the discrete logistic model oscillates about the equilibrium, P_e = M, but the solution grows away from this equilibrium. ( r > 3 results in negative solutions.

To see a specific example with numbers go to the Worked Examples section.

Height of the Ball Revisited

For a specific example, let us consider a ball that is thrown vertically with a initial upward velocity of 64 ft/sec (so v₀= 64). The acceleration due to gravity is g = 32 ft/sec². Find how high this ball travels. There are two good ways to solve this problem. From our knowledge of the height function being a quadratic, we could simply find the vertex of the parabola, knowing that it must be at the top of the flight of the ball. Another physical property that can be used to find this maximum for flight of the ball is to recognize that at the top of its flight the ball is temporarily stopped, then its velocity becomes negative as the ball falls back to the ground. Thus, finding the time when the velocity is zero gives the time of the maximum height of the ball. With the specific numbers we have given above, the height of the ball satisfies

The velocity function from our differentiation rules is

Solving the velocity equal to zero, 64 - 32 t = 0, gives t = 2 sec. To find the maximum height of the ball, this time is substituted into the original height equation, so

Maxima, Minima, and Critical Points

The example above shows that finding when the derivative is zero can give important information about the graph of a function. Another way to view this phenomenon is to examine any graph of a smooth function (which is a function that is continuous and differentiable). It is clear that when you are at a high point of the graph (that is not an endpoint), then the tangent line must be horizontal, which says that the derivative is zero.

Definition: A smooth function f(x) is said to be increasing on an interval (a,b) if f '(x) > 0 for all x in the interval (a,b). Similarly, a smooth function f(x) is said to be decreasing on an interval (a,b) if f '(x) < 0 for all x in the interval (a,b).

A high point of the graph is where f(x) changes from increasing to decreasing, while a low point on a graph is where f(x) changes from decreasing to increasing. In either case, the derivative passes through zero.

Definition: A smooth function f(x) is said to have a local maximum at a point c, if f '(c) = 0 and f '(x) changes from positive to negative for values of x near c. Similarly, a smooth function f(x) is said to have a local minimum at a point c, if f '(c) = 0 and f '(x) changes from negative to positive for values of x near c.

Clearly, it is important to find where the derivative is zero to find these highest and lowest points on a graph.

Definition: If f(x) is a smooth function with f '(x_c) = 0, then x_c is said to be a critical point of f(x).

Finding critical points helps find the local high and low points on a graph, but some critical points are neither maxima or minima.

Graphing Polynomials

We have applied these definitions to a simple quadratic for the height of a ball in flight. Let us examine how finding critical points can help us graph other polynomials. Consider the following examples.

Example: Suppose that

f(x) = x³ - 6x² - 15x + 2.

Use the information to help sketch a graph of f(x).

Solution: We begin by taking the derivative,

f '(x) = 3x² - 12x - 15 = 3(x + 1)(x - 5).

The derivative is zero when x_c = -1 or 5. Evaluating the function at the critical points, we find f(-1) = 10, which gives a local maximum at (-1,10), and f(5) = -98, which gives a local minimum at (5,-98). The y-intercept is (0,2) another easy point to add to our graph, so we now have good information to make a reasonable sketch of the graph, which is shown below. Note that since this is a cubic equation, the x-intercepts are very hard to find.

 

 The Second Derivative and Concavity

Since the derivative is itself a function, then if it is differentiable, one can take its derivative to find the second derivative often denoted f ''(x). The sign of the second derivative tells where the first derivative is increasing or decreasing. If the first derivative is increasing or the second derivative is positive, then the original function is getting "steeper." The function is said to be concave upward. If the first derivative is decreasing or the second derivative is negative, then the original function is said to be concave downward. Thus, the second derivative is a measure of the concavity of a function. For our smooth functions described above, we can see that maxima generally occur where the function is concave downward, while minima occur where the function is concave upward. This property is often summarized in the following test.

The Second Derivative Test. Let f (x) be a smooth function. Suppose that f '(x_c) = 0, so x_c is a critical point of f. If f ''(x_c) < 0, then x_c is a relative maximum. If f ''(x_c) > 0, then x_c is a relative minimum.

Example: If we return to our example above where f(x) = x³ - 6x² - 15x + 2, then we see that the second derivative is

The critical points occurred at x_c = -1 and 5. Evaluating the second derivative at the critical point x_c = -1, we find f ''(-1) = -18, which says the function is concave downward at -1, so this is a relative maximum. Similarly, the second derivative at the critical point x_c = 5 is f ''(5) = 18, which says the function is concave upward, so this is a relative minimum.

Points of Inflection

When the second derivative is zero, then the function is usually changing from concave upward to concave downward or visa versa. This is known as a point of inflection. A point of inflection is where the derivative function has a maximum or minimum, so the function is increasing or decreasing most rapidly. From an applications point of view, if the function is describing a population, then the point of inflection would be where the population is increasing or decreasing most rapidly. That is, the point of inflection measures when the change of a function is its greatest or smallest.

From a graphing perspective, the point of inflection shows the visual change in concavity. It is not nearly as important as extrema, but does provide one more point to aid in graphing the function.

Example: Once again returning to our example above of f(x) = x³ - 6x² - 15x + 2, where the second derivative is f ''(x) = 6x - 12, we can easily find the point of inflection. We see that f ''(x) = 0 when x = 2. Thus, the point of inflection occurs at (2, -44). This can be see on the graph above.

As usual, for more Worked Examples use this hyperlink.