Math 121 - Calculus for Biology I
Fall Semester, 2003
Derivative of ex and ln(x)
San Diego State University -- This page last updated 08-Jan-03
|
|
Math 121 - Calculus for Biology I |
|
|---|---|---|
|
|
San Diego State University -- This page last updated 08-Jan-03 |
|
Drugs have long been administered by either a pill or an injection. The result is that the body receives a fairly high dose rapidly, then the drug remaining in the blood disappears in an exponentially decaying manner. Recently, scientists have invented polymers that can be implanted to deliver a drug or hormone for a much longer period of time. For example, there are several long term birth control devices that are injected just below the skin. These devices deliver the hormones estrogen and progesterone at sufficiently high levels for extended periods of time to prevent pregnancy. These new drug delivery devices are a hot area of research for a variety of medical conditions. These devices could aid diabetes sufferers with a more uniform level of insulin or they could deliver chemotherapeutic drugs to cancer patients over a much longer period of time at lower doses to maximize their efficacy.
Typically, these drug delivery devices have a long time period of decaying release of a drug or hormone, while the body clears the drug or hormone out relatively quickly. Mathematically, this is described by two decaying exponentials. Let the delivery of a drug by a new polymer device be described by the function
where c(t) is the concentration of the drug and C0, r, and q are constants depending on the drug delivery system with q > r. C0 is a constant that indicates the level of the drug or hormone trapped in the polymer delivery device. The kinetic constants r and q are associated with the decay of the polymer that releases the drug and the degradation of the drug in the body of the patient, respectively. We would like to know the maximum level of drug that is delivered by this device and how long the drug level stays above some certain level.
As an example, suppose that the concentration of a drug satisfies
where the c(t) is a concentration in mg/dl and the time t is in days. We would like to find when the maximum concentration of the drug is being delivered and how high that level is. We might also need to know how long the drug stays above a certain level to maintain effectiveness. The maximum is often needed to study toxic effects. Below is a graph of our example.
The exponential function ex is a special function in that it's the only function (up to a scalar multiple) that is the derivative of itself. That is
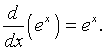
Note that by our scalar multiplication rule, then the derivative of f(x) = kex is f '(x) = kex.
From the definition of the derivative and using the properties of exponentials, we see that
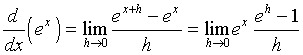 .
.One definition of the number e is the number that makes
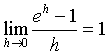
Geometrically, the function ex is a number raised to the power x, whose slope of the tangent line at x = 0 is 1.
The derivative of ekx is given by
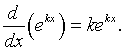
Example 1: Find the derivative of
Solution: From our rule of differentiation and the formula above, we have
Example 2: Consider the example of the drug delivery system given above. Find the maximum for this function.
Solution: The function is given by
so the maximum is found by taking the derivative of this function and setting it equal to zero. From the differentiation rule for the exponential given above, we have
To find the maximum we must solve
So
Thus, t = ln(20)/0.19 = 15.767 days. The maximum occurs at c(15.767) = 8.11 mg/dl. This can be seen on the graph above.
Height and Weight Relationship for Children
The average height and weight of girls is given in the table below.
|
age(years)
|
height(cm)
|
weight(kg)
|
|
5
|
108
|
18.2
|
|
6
|
114
|
20.0
|
|
7
|
121
|
21.8
|
|
8
|
126
|
25.0
|
|
9
|
132
|
29.1
|
|
10
|
138
|
32.7
|
|
11
|
144
|
37.3
|
|
12
|
151
|
41.4
|
|
13
|
156
|
46.8
|
Ehrenberg noted that there was a logarithmic relationship between the height and the weight of children. Below is a graph of the data above, showing the height as a function of weight of girls ages 5 through 13 using data on the average height and weight of girls in the U. S.

The formula for the height, H, as a function of weight, w, is given by
H(w) = 49.5ln(w) - 34.14.
We would like to find the find the rate of change of height with respect to weight for the average girl.
We cannot easily use the definition of the derivative to find the derivative of the natural logarithm. The derivative of the natural logarithm, ln(x), is given by the formula
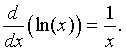
This relationship is most easily demonstrated after learning the Fundamental Theorem of Calculus in Math 122, which centers about the integral.
Derivative of the Height and Weight Relationship for Children
The relationship given above is easily differentiated with respect to w, using the derivative for the natural logarithm. It follows that
![]()
From this relationship, it is clear that as the weight increases, the rate of change in height decreases. Note that this is not the rate of change of the height as a function of the age, which we saw to be nearly linear in the first section of the lecture notes.
Example 3: Find the derivative of
Solution: From our properties of logarithms and the formula above, we have f(x) = ln(x2) = 2ln(x), so
f '(x) = 2/x.
There are a collection of Worked Examples to help you understand this material and aid with the homework problems.