specialeg

Math 121 - Calculus for Biology I
Fall Semester, 2003
Derivative of e^x and ln(x) - Examples

© 2001, All Rights Reserved, SDSU & Joseph M. Mahaffy
San Diego State University -- This page last updated 18-Nov-02

The Derivative of e^xand ln(x) -Examples

Differentiation of Exponentials and Logarithms
Graphing Exponentials and Logarithms
Growth of Bacteria
Radioactive Decay
von Bertalanffy Equation

The main lecture page worked through some examples of differentiation of the exponential and logarithm functions. It also went through an example of drug concentration. Below we show a few more differentiation examples, then show how differentiation can be used to find rates of change of population and rates of decay.

Example 1: Find the derivatives of the following functions:

Solution: We begin with the derivative of f(x). The rules of differentiation give

f '(x) = 4(2e²^x) = 8e²^x.

For g(x), we first use the properties of logarithms to change the expression so that it only includes ln(x)

Graphing Exponential and Logarithms

Example 2: Consider the following function

y = 2e^-0.2^x- 1.

Graph this function and find its derivative.

Solution: The domain of this function is all values of x. The y-intercept satisfies

2e^-0.2(0)- 1 = 1.

The x-intercept satisfies

2e^-0.2^x- 1 = 0

2e^-0.2^x= 1

e^0.2^x= 2

x = 5 ln(2) = 3.466

For large values of x, the exponential function decays to zero. Thus, there is a horizontal asymptote to the right with

y = -1.

The graph of the function is given by

The derivative of this function satisfies

y' = 2(-0.2) e^-0.2^x = -0.4 e^-0.2^x.

Since the exponential function is always positive, the derivative is always negative though the derivative does approach zero as x becomes large (approaching the horizontal asymptote). Thus, this function is always decreasing, which is clearly shown in the graph.

Example 3: Consider the following function

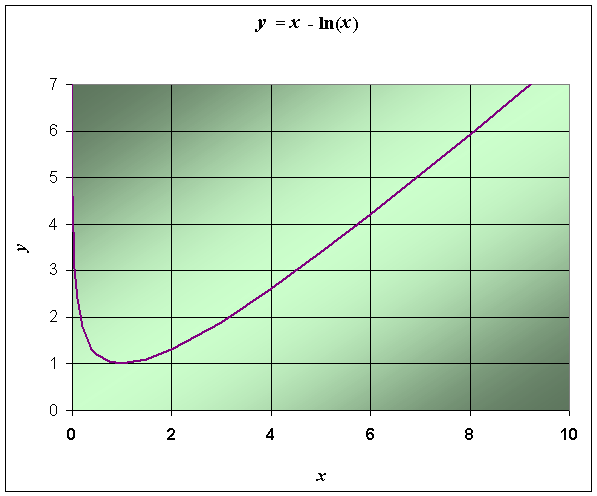
y = x - ln(x) .

Find the first and second derivatives of this function. Find any local extrema, then graph the function.

Solution: The derivative for this function is given by

The second derivative is given by

Graphing the Function:

This function is only defined for x > 0. Thus, there is no y-intercept. However, there is a vertical asymptote at x = 0.

We find extrema by setting the derivative equal to zero. The derivative is zero only when the numerator of the above expression for the derivative is zero, so x = 1. This gives an extremum at (1, 1).

Since the second derivative is always negative, which says that this function is concave upwards. It follows that the extremum computed above is a minimum.

The graph of the function is given by

Example 4: Suppose that culture of Escherichia coli begins with 100,000 bacteria. Assume that this culture is doubling every 30 minutes. Find the rate of change in number of bacteria per minute at 5, 10, 40, and 60 minutes. Also, find the number of bacteria at these times.

Solution: Any culture that is doubling over a fixed period of time is growing exponentially. The first step in this problem is to find the population of bacteria in terms of the exponential function. Since the population starts at 100,000, we can write the population as a function of time as

P(t) = 100000 e^at,

where we need to determine the constant a. If the population doubles in 30 minutes, then we know that

P(30) = 200000 = 100000 e³⁰^a or e³⁰^a = 2.

By taking the natural log of both sides, we see that

30a = ln(2) or a = ln(2)/30 ~ 0.0231.

Thus, we can write the expression for the population as

P(t) = 100000 e^t ^ln(2)/30~ 100000 e^0.0231^t.

It is easier to work with this expression leaving the parameter a in the expression until we want the numerical answer, so we'll mostly work with the original expression (which helps carry to other problems of the same sort). To find the rate of change in the number of bacteria at a given time, we need the derivative of the population, so from the rule for differentiating the exponential function, we have

P '(t) = 100000ae^at.

To find the rate of change in number of bacteria at t = 5 and the population at that time, we compute

P '(5) = 100000ae⁵^a~ 2310 e^0.1155~ 2593 bacteria/min.

P(5) = 100000 e⁵^a~ 100000 e^0.1155~ 112,200 bacteria

Similarly, we find the rate of change in number of bacteria at t = 10, 40, and 60, and the population at those times.

P '(10) = 100000ae¹⁰^a~ 2310 e^0.231~ 2910 bacteria/min.

P(10) = 100000 e¹⁰^a~ 100000 e^0.231~ 126,000 bacteria

P '(40) = 100000ae⁴⁰^a~ 2310 e^0.924~ 5820 bacteria/min.

P(40) = 100000 e⁴⁰^a~ 100000 e^0.924~ 251,900 bacteria

P '(60) = 100000ae⁶⁰^a~ 2310 e^1.386~ 9240 bacteria/min.

P(60) = 100000 e⁶⁰^a~ 100000 e^1.386~ 399,900 bacteria

Thus, we see both the number of bacteria and the rate of growth increasing with increasing time.

Example 5: Naturally-occurring potassium is not radioactive, but radioactive isotopes can be manufactured from natural potassium. Potassium isotope 43 decays at a rate proportional to the amount of the radioactive potassium available. After it emits a beta ray, it reverts to calcium. (⁴³K goes through a b- decay with a neutron changing to a proton to produce ⁴³Ca.) This can be used as a tracer for studying the effectiveness of potassium absorption in the body.

Suppose we begin with a 10 mg sample of a radioactive substance that is giving 3000 counts/min (cpm) of beta radiation. If this substance has a half-life of 20 hours, then find the rate of change in the amount of the radioactive substance and the expected counts/min of beta radiation after 5, 10, and 15 hours.

Solution: If a radioactive substance has a half-life of x hours, then it decays exponentially to half its original amount in x hours. Let R(t) be the amount of the radioactive substance, then an expression for the amount of the radioactive substance is given by

R(t) = 10 e^-kt,

where the constant k must be determined based on the half-life. If the amount R(t) drops to 5 mg in 20 hours, then we know that

R(20) = 5 = 10e^-20^k or e^-20^k = 1/2 or e²⁰^k = 2.

By taking the natural log of both sides, we see that

20k = ln(2) or k = ln(2)/20 ~ 0.03466.

Thus, we can write the expression for R(t) as

R(t) = 10 e^-t ^ln(2)/20~ 10 e^-0.03466^t.

As in the previous example, it is easier to work with this expression using the parameter k until we want the numerical answer, so we'll mostly work with the original expression (which helps carry to other problems of the same sort). To find the rate of change in the amount of R(t) at a given time, we need the derivative of R(t). From the rule for differentiating the exponential function, we have

R '(t) = -10ke^-kt.

To find the rate of change in the amount of radioactive substance at t = 5 hours, we compute

R '(5) = -10ke^-5^k~ -0.3466 e^-0.1733~ -0.2915 mg/h.

The problem states that 10 mg of R(t) gives 3000 cpm, so each mg of R(t) will give off 300 cpm of beta radiation. Thus, to find the level of beta radiation at t = 5 hours, we must compute

R(5) = 10e^-5^k~ 10 e^-0.1733~ 8.41 mg,

So the amount of beta radiation will be

300 R(5) cpm = 2523 cpm.

Similarly, we find the rate of change in the amount of R(t) at t = 10 and 15 hours, and the amount of beta radiation at those times.

R '(10) = -10ke^-10^k~ -0.3466 e^-0.3466~ -0.2451 mg/h.

with the amount of beta radiation being

300 R(10) = 3000e^-10^k~ 3000 e^-0.3466 = 2121 cpm.

At t = 15,

R '(15) = -10ke^-15^k~ -0.3466 e^-0.5199~ -0.2061 mg/h.

with the amount of beta radiation being

300 R(15) = 3000e^-15^k~ 3000 e^-0.5199 = 1784 cpm.

Example 6 (von Bertalanffy Equation): As a fish ages, it reaches a maximum size. A model for fish growth was developed by von Bertalanffy, which has an exponential solution.

a. Data shows that on average a lake trout takes 5.5 years to reach 2 kg and 15 years to reach 5 kg. When these data are fit to the von Bertalanffy equation, an equation for weight as a function of age is given by

W(a) = 20.2(1 - e^-0.019^a).

Find the rate of change of weight, W, with respect to the age, a. Graph the solution of the von Bertalanffy equation showing the intercepts and any asymptotes.

b. Solve the above equation for age, a, as a function of the weight, W. Differentiate this function, finding the rate of change of age with respect to weight. Graph this function showing any intercepts and asymptotes.

Solution: a. Write the von Bertalanffy equation as follows,

W(a) = 20.2 - 20.2 e^-0.019^a

then differentiating with respect to the age, a, gives

This says that the function is monotonically increasing (as we would expect for growth of a fish).

This equation goes through the origin, and it is easy to see that for large values of a the exponential decays to zero, which implies that asymptotically the fish grows to a weight of 20.2 kg. This is the horizontal asymptote. Below is a graph of the von Bertalanffy equation

b. Next solve the equation

W = 20.2 - 20.2 e^-0.019^a

for the age, a. It follows that

Thus, we can write the age, a, as a function of the weight, W. It is given by

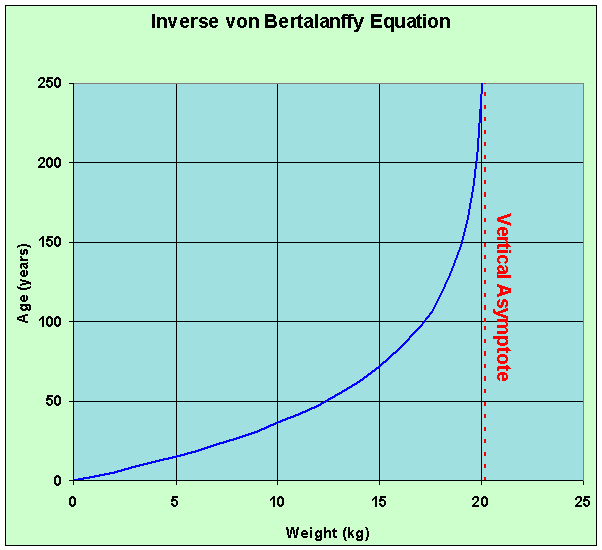
a(W) = 158.2 - 52.63 ln(20.2 - W).

Unfortunately, this expression cannot be directly differentiated without the chain rule (to be learned soon). However, try a substitution of Z = 20.2 - W. (Note that dZ/dW = -1, which is just a sign change.) With this substitution, we have

a(Z) = 158.2 - 52.63 ln(Z),

and

We will find with the chain rule that

Since Z = 20.2 - W and dZ/dW = -1, the formula gives

The graph of the inverse function for the von Bertalanffy equation given by a(W) has a domain of W < 20.2. There is a vertical asymptote at W = 20.2. The derivative above shows that this function is strictly increasing. Since the function W(a) passes through the origin, its inverse function also passes through the origin

a(0) = 158.2 - 52.63 ln(20.2) = 0.

Below is the graph of this inverse function.