1. Chemostat with Two Yeast Populations
2. Malthusian Growth Model
   1. Continuous Malthusian
   2. Solution of the Continuous Malthusian Growth Model
   3. Fitting the Continuous Malthusian Growth Model
3. References

This course begins with a study of yeast competing for a limited source of nutrient. (Population models are covered in the second section of the text.) This section starts with a description of the Gause yeast experiments. Based on the experiments, several mathematical models are discusssed with the techniques required to study them. The models are fit to the data, then a discussion of the qualitative behavior of the models is presented.

Chemostat with Two Yeast Populations

One method for maintaining a culture of yeast used in brewing beer is to create a chemostat. A chemostat is a large vat, where nutrients are pumped into the vat with a constant flow rate, then the growing culture is removed at the same flow rate. Under ideal conditions, a monoculture of yeast grows exponentially at first, then as the population becomes sufficiently large, the concentration of yeast levels off. At a certain level, known as the carrying capacity, the population of yeast balances the supply of nutrient entering the vat. At this stage, the the population (or concentration) of yeast remains constant with as many yeast being born in each unit of time as are flushed out from the chemostat per unit time. These conditions guarantee a constant supply of uniform concentration of the yeast flowing from the chemostat. This allows the brewmaster a consistent supply of the yeast culture, which ensures a uniform product with the desired characteristics. Unfortunately, it is almost impossible to keep a consistent monoculture of the yeast. The vat often gets infected with a competing yeast or bacteria that destroys the uniformity and lowers the quality of the beer. Below is a cartoon illustrating the idea of a yeast culture growing in a chemostat.

Ideally, we would like to develop a mathematical model for the chemostat described above, especially when a contaminating species invades the culture. We begin with an analysis of some classical studies from the 1930s that carefully examine cultures of yeast that have a fixed supply of nutrient. In the book Struggle for Existence, G. F. Gause [1] describes his experiments, which do not use an actual chemostat, but rather changed the nutrient in a closed vessel regularly (every 3 hours). This is roughly equivalent to a chemostat. He performed a number of experiments to test competition of microbial species. One set of experiments examined the standard brewers yeast, Saccharomyces cerevisiae, and a slower growing yeast, Schizosaccharomyces kephir. He tested these organisms in monocultures to find their growth parameters with his experimental set up, then he mixed the cultures to determine how the organisms reacted when they competed in the same nutrient medium. He notes that though he used a standard medium, he was not certain of all the concentrations of the different components in the medium, which complicates the ecological model since the species could be utilizing different components of the medium.

Below we present a series of tables showing the two yeast species competing in the Gause experiments. The first table combines two experiments of Gause using only S. cerevisiae in the culture. These data are shifted by 6 hours from the original experiment because no data were collected until 6 hours from innoculation of the yeast culture. The innoculation is said to be a single drop from a culture that had been growing for 72 hours and assumed to be at carrying capacity. Notice that Gause measured the volume of the yeast rather than the population, which is probably a better measure of the organism's ability to absorb the nutrients. The volume quoted in the papers only indicated units marked on a centrifuge tube after spinning the culture down, so absolute units are not available.

Time (hr)	0	1.5	9	10	18	18	23	25.5	27	34	38	42	45.5	47
Volume	0.37	1.63	6.2	8.87	10.66	10.97	12.5	12.6	12.9	13.27	12.77	12.87	12.9	12.7

The second table combines two experiments of Gause using only S. kephir in the culture. To match with the data for the experiment with S. cerevisiae, these data are also shifted by 6 hours from the original (which had the first measurement at 15 hours after innoculation). These data are collected over a much longer time period because of the slow growing nature of S. kephir.

Time (hr)	9	10	23	25.5	42	45.5	66	87	111	135
Volume	1.27	1.0	1.7	2.33	2.73	4.56	4.87	5.67	5.8	5.83

Finally, we present a table that shows the competition of S. cerevisiae and the slower growing S. kephir that Gause performed in two experiments. Once again the data are shifted by 6 hours from the original experiment to match the first time when data was actually collected after innoculation of the yeast cultures.

Time (hr)	0	1.5	9	10	18	18	23	25.5	27	38	42	45.5	47
Volume (S. cerevisiae)	0.375	0.92	3.08	3.99	4.69	5.78	6.15	9.91	9.47	10.57	7.27	9.88	8.3
Volume (S. kephir)	0.29	0.37	0.63	0.98	1.47	1.22	1.46	1.11	1.225	1.1	1.71	0.96	1.84

We are now presented with a collection of raw data and would like to explain these data with a mathematical model for the growth of yeast.

How do we create a mathematical model from these data?

In a previous lecture, we developed the discrete Malthusian growth model, which is considered the simplest mathematical model for the dynamic growth of a population.

The discrete Malthusian growth model discussed before had the form

P_n+1 = (1 + r)P_n,

where P_n is the volume of the yeast at time n (with this time being 1/2 hour units) and r is the rate of growth (per 1/2 hour). This equation can be rearranged to give

which says that the change in volume of the yeast between the (n + 1)^st time period and the n^th time period is proportional to the volume of the yeast at the n^th time period.

Now we want to write this model in terms of continuous time variables. Define P(t) to be the volume of the yeast at any time t. Assume that r is the rate of change of the volume of the yeast per unit time per unit volume of the yeast. If we let Dt be a small interval of time, then the change in volume of the yeast between t and t + Dt, satisfies the equation

Biologically, this equation says that the change (difference) in the volume of the yeast over a small period of time is found by taking the rate of growth times the volume of the yeast times the interval of time Dt. The equation above can be rearranged to give

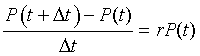
The right hand side of the equation readily transforms into a derivative as we take the limit of Dt tending toward zero. Thus, in the limit this model reduces to the differential equation

This is the continuous Malthusian growth model.

Solution to the Malthusian Growth Model

The differential equation describing the continuous Malthusian growth model says that the derivative of an unknown Population function P(t) is equal to a constant times the unknown Population function. (The rate of change of a population is proportional to the population.) The only function that we know that is a derivative of itself is the exponential function. We try a solution of the form

where c is an arbitrary constant. But P '(t) is cre^rt, which is rP(t), so satisfies the differential equation. If we add an initial condition P(0) = P₀, then the unique solution becomes

This is another reason why Malthusian growth is often called exponential growth. This solution is equivalent to the solution of the discrete Malthusian growth model with the exception that the time is in units of hours, which corresponding affects the growth rate ^r.

Fitting the Continuous Malthusian Growth Model

The fitting of this model is equivalent to the fitting of the discrete Malthusian growth model with the only change being the units of time and the formula that is used. If we repeat the curve fits above, then we obtain the following continuous Malthusian growth models.

Algebraic fit to the data

We use the first and third data points for S. cerevisiae, (t, P) = (0, 0.37) and (t, P) = (9, 6.2) to fit the continuous Malthusian growth model and find the parameters P₀ and r. From the model, the first data point gives

The third data point gives

It follows that

so the continuous Malthusian growth model satisfies

Exponential fit (Linear least squares best fit to logarithm of data)

Again we take the first 4 data points from the data on S. cerevisiae, then fit the best straight line through the logarithm of the data. The best straight line fit to the logarithm of the volume data is given by

It follows that

Thus, the best continuous Malthusian growth model is given by

Nonlinear least squares best fit

Finally, we again minimize the sum of the square error between the data and the continuous Malthusian growth model. For the first data points on S. cerevisiae, the least squares functional is given by

where

The solution to this minimization problem give the parameters

Thus, the best Malthusian growth model for this nonlinear least squares fit is given by

These solutions are completely equivalent to the discrete cases above. Another Excel worksheet is provided by a hyperlink to see the computations. A graph of these models with the data would match the graph above for the discrete Malthusian growth model, except that scale on the horizontal axis would have a factor of 1/2.

References

[1] G. F. Gause, Struggle for Existence, Hafner, New York, 1934.

[2] G. F. Gause (1932), Experimental studies on the struggle for existence. I. Mixed populations of two species of yeast, J. Exp. Biol. 9, p. 389.