SDSU

Math 636 - Mathematical Modeling
Fall Semester, 2009
Discrete SIR Models - Epidemiology

 © 2001, All Rights Reserved, SDSU & Joseph M. Mahaffy
San Diego State University -- This page last updated 16-Sep-09

Discrete SIR Models - Epidemiology

     
  1. Information on Influenza
  2. SIR Model
  3. Controlling Flu
  4. Model Analysis
  5. References

Influenza

Influenza or flu is a viral infection that is readily transmitted through the air and causes respiratory problems in humans and other animals. It occurs seasonally and results in an average of 30,000 deaths in the U. S. annually primarily among the young and old. There have been some epidemics, such as the pandemic of 1918, which  resulted in over 30 million deaths around the world. 

There are two primary types, A and B of influenza, which appear seasonally, usually starting in the fall and continuing through the winter months. These types mutate creating new strains each year. Flu is an RNA virus with 11 genes that mutate regularly, making it difficult to create general vaccines. Each year scientists anticipate the most likely dominant strain and determine which mutant is most likely to spread in order to create a vaccine to protect the population. In addition to the many deaths, this disease results in huge economic losses from lost work and treatment of fragile patients.

Below we provide data from the Center of Disease Control for one season of flu. The table below gives the number of cases week by week for a control set of individuals. In particular, we consider the data for the cases with Type A for the flu season in 2004 and 2005, where 99.7% of these cases were influenza A (H3N2) viruses. These data come from 157,759 samples that were tested amongst people exhibiting flu-like symptoms. The first week, n = 0, corresponds to the last week in September, which is near the seasonal start of the flu season in the U. S. 

n (wk) In n (wk) In n (wk) In
0 3 17 1096 34 2
1 2 18 1354 35 0
2 7 19 1335 36 2
3 12 20 1109 37 1
4 9 21 936 38 6
5 10 22 627 39 0
6 27 23 476 40 0
7 21 24 295 41 1
8 36 25 164 42 0
9 63 26 94 43 0
10 108 27 37 44 0
11 255 28 26 45 1
12 472 29 15 46 0
13 675 30 8 47 3
14 580 31 5 48 0
15 844 32 3
16 974 33 1


SIR Model for Influenza

Influenza is a disease that follows a classic mathematical model known as an SIR model. The population can be divided into susceptible, infected, and recovered individuals. Once a person has a particular strain of one of the types of the influenza virus, then that individual develops immunity to that specific strain, preventing reinfection. (This is why flu viruses need to mutate to keep finding new hosts.) Since flu acts over a very short period of time, we will simplify our model by assuming that the population remains constant with a size of N. This means that it is sufficient to simply keep track of two classes of individuals, the susceptibles, Sn, and the infected, In, as the recovered satisfy 

Rn = N - Sn - In,


Since we are ignoring births and deaths in the population, we only consider the spread of the disease, which is based on successful contacts (such as inhaling aerosol infected particles from the sneeze of an infected individual into the lungs of a susceptible host). The discrete mathematical model is given by the system of equations:

Sn+1 = Sn - (b/N)SnIn,

In+1 = (1 - g)In + (b/N)SnIn,


where bS/N represents the proportion of contacts by an infected individual that result in the infection of a susceptible individual. The parameter g  is the probability that an infected person recovers (enters class R of the SIR model). The ratio 1/g  is the average length of the infectious period of the disease. 

Modeling Assumptions

The SIR model above is a discrete dynamical system, where populations are exmined at discrete time steps. The model assumes that the population is well-mixed, so all individuals are equally likely to encounter other individuals. This probably works well for local populations, such as a particular school, but is not good for the entire U. S., where these data are collected. It is well known that there are significant regional outbreaks, and often containing regional outbreaks is key to controlling a disease.

The model also assumes that an individual becomes infectious as soon as he or she becomes infected, when in fact there are often time delays inherent in a disease. This factor is sometimes modeled with an SEIR model, where E represents exposed individuals. This simplistic model doesn't account for many factors that could prove important in the course of the disease, yet it gives some understanding of the disease and how we might affect its spread.

Modeling Simulation

We want to simulate the SIR model and try to fit it to the CDC data in the table above. Assume that  the control population consists of N = 157,759, which is based on the number of samples that the CDC analyzed. This is obviously not representative of a well-mixed homogeneous population. However, it would be very difficult to obtain a good choice for N. With this assumption for our population, it becomes natural to take I0 = 3 and S0 = 157,756 =  N - I0. We would like to simulate the model and determine the best values of the parameters, b and g, that match the data from the CDC data. These parameters are key to understanding the nature of a disease.

Epidemiologists often examine what is called the basic reproduction ratio given by 

R0 = b/g,

which provides a measure of how rapidly a disease will spread and how much of the population will be affected by a particular disease. Also, the average length of the infectious period is equal to 1/g.

We simulate the model, finding the Least Sum of Square Errors (LSSE) by changing the parameters, b and g. The SSE is found between the CDC data on the infecteds and the model simulation of In. Using Excel's Solver, we obtain a LSSE = 155,083, and the best parameter values are:

b = 3.993 and g = 3.517.

The fit is seen below in the graph of the model and data. (See Excel Sheet.)



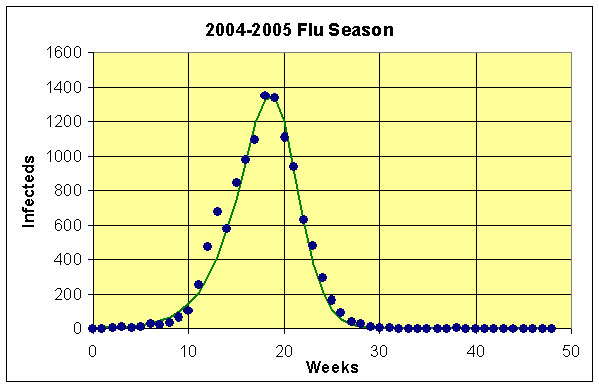
By taking the inverse of g, we find that the average duration of the infectious period is 1.99 days. The basic reproduction ratio is

R0 = 1.135.

To determine the impact of a particular flu season, we want to know the total number of individuals who were infected by the influenza virus. Since we are assuming a constant population N and because the number of infected individuals is essentially zero at the end of the simulation. We estimate the total number of cases of flu by computing the number in the recovered class, so 

Rn = N - Sn = 39,001,

for n large. This represents approximately 24.7% of the population.

 Controlling the Flu

The CDC is interested in minimizing the impact of flu on the population, so uses a number of different controls. We examine three different controls that are employed to fight outbreaks of the flu. 

The first line of defense, of which you are undoubtedly aware, is the annual flu vaccine. The effect of a vaccine is to lower the population of susceptible individuals, which is terms of our model is simply to lower S0 by moving a number of individuals to R0. (In fact, many individuals already have immunity to a given strain of the flu because of earlier contact with a related strain.) Suppose we vaccinate 5% of the total population at the very beginning of the flu season (assuming that the vaccine is 100% effective). This immediately shifts some of the population to the recovered individuals in the model. We calculate the initial susceptible population by 

S0 = 0.95N - I0,
R0 = 0.05N

Assuming no other changes for this epidemic, then the values of g and b remain the same as above. We simulate the SIR model with this new initial condition. (See the graph below.) The effect is to delay the onset of the flu epidemic and dramatically reduce the number of people who become infected. The total number of people becoming infected is now 

Rn = N - Sn = 22,311,

for n large. This represents approximately 14.1% of the population, so the number getting the flu about 60% of the number had there been no treatment.

A second method of control is the quarantine of infected individuals or the education of the public on how to lessen the contact between infected
and susceptible individuals (improve hygiene). This lowers the value of b. Suppose we lower the value of b by 5%, which is equivalent to multiplying the best fitting value of b found above by 0.95. We use the original initial conditions and best fitting value of g  and this new b value to simulate the SIR model. (See graph below.) Once again, the effect is to delay the onset of the flu epidemic and dramatically reduce the number of people who become infected. This simulation is very similar to the one for vaccination. The total number of people becoming infected is now 

Rn = N - Sn = 23,483,

for n large. This represents approximately 14.9% of the population, so the number getting the flu again about 60% of the number had there been no treatment.

The final control that we employ is the use of Oseltamivir or Tamiflu, which is a drug that shortens the symptoms of flu for many people. If we assumes that this drug shortens the length of the period of infectivity of the infected individuals, then this can be modeled by increasing g. Suppose we increase the value of g  by 5%, which is equivalent to multiplying the best fitting value of g  found above by 1.05. We use the original initial conditions and best fitting value of b to simulate the SIR model. Once again, the effect is to delay the onset of the flu epidemic (though not quite as much) and dramatically reduce the number of people who become infected. The total number of people becoming infected is now 

Rn = N - Sn = 24,305,

for n large. This represents approximately 15.4% of the population, so the number getting the flu again about 60% of the number had there been no treatment. Thus, all of the proposed treatment options are similarly effective and significantly affect the outbreak of the flu epidemic.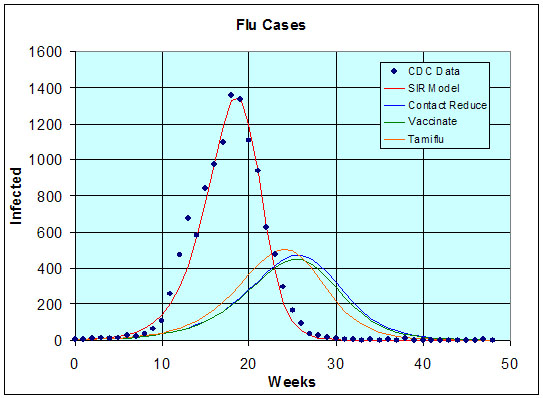

Controlling Flu



Compare and contrast the different approaches to controlling a flu outbreak. Give advantages and disadvantages of each of the controls. Include a discussion of the practicality and financial burden of each of these approach. Give a couple of strengths and weaknesses for this SIR model. Select another disease that satisfies the SIR model and discuss how this lab applies to treatment of the disease you are considering. How does this study apply to elimination of other serious diseases? 

Analysis of SIR Model

Finding the Equilibria

We find equilibria by setting Sn+1 = Sn = Se and In+1 = In = Ie. When we substitute into the first equation, we find

Se = Se - (b/N)SeIe,

which yields

(b/N)SeIe = 0

Se = 0 or Ie = 0.

The second equation gives

Ie = (1 - g)Ie + (b/N)SeIe,

so

gIe = (b/N)SeIe.

If Se = 0, then necessarily Ie = 0. If Ie = 0, then Secan be anything. It follows that the equilibria are

Ie = 0 and  0 < Se < N.

Linearizing about the Equilibria

We quickly review the linearization of a system given by:

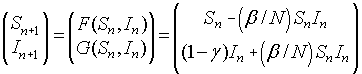
The Jacobian matrix is given by

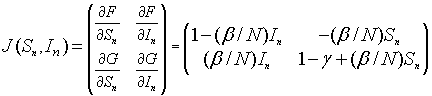
The linearized system for the SIR model about the equilibrium (Se, Ie) = (Se, 0) is given by the linear discrete system:

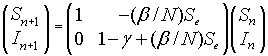
Since this is an upper triangular matrix, the eigenvalues are given by the diagonal elements. One eigenvalue is l1 = 1, while the other eigenvalue satisfies

l2 = 1 - g + (b/N)Se.

For the equilibrium to be unstable and the disease to spread, we need l2 > 1 or 1 - g + (b/N)Sn > 1. Thus,

bSn/N > g

.

We see that if R0 > 0 and Sn ~  N, then the disease will spread. However, as Sn gets smaller with more people establishing immunity, then N/Sn > b/g and the disease dies out.

 

References [1] CDC Flu website - www.cdc.gov/flu/ Specifically for data: www.cdc.gov/flu/weekly/fluactivity.htm (last visited Sept. 2009). 
[2] Wikipedia - en.wikipedia.org/wiki/Influenza (last visited Sept. 2009).