Session #2 - Sequences and Series. Fourier series. Matrices, including basic operations, solving linear systems, and eigenvalues and eigenvectors. Hyperlink to a special worksheet organization webpage (with its Maple worksheet).

This session expands the list of commands in Maple. We begin with sequences and series, showing how Maple can significantly simplify handling these entities. We follow with a section that gives an introduction to using Maple for linear algebra with a few basic operations. A hyperlink allows you to download the Maple worksheet. Another hyperlink gives organizational information about Maple sections (along with its Maple worksheet).

When you download a Maple worksheet or open a saved worksheet from previous work, then all of the work is shown. However, none of the variables and functions are active until you enter the line containing that line. An easy way to activate the entire worksheet to proceed from where you left off in your work is to Execute the entire worksheet. This is easily done by going to Edit on the menu bar and selecting Execute, then choosing Worksheet.

Maple provides an excellent tool for handling sequences and series. Below we examine some Calculus problems from this area, which classically gives students so much difficulty, and can be computationally very intensive. We begin with the sequence (seq) command. This command is often valuable for storing information to later be graphed.

> seq(n^2/(3-n^2), n = 0..10);

The limit of the sequence can be easily found using the limit command in Maple.

> limit(n^2/(3-n^2), n = infinity);

To visualize the sequence, we create a sequence of ordered pairs, which can then be plotted. In the plot command, we have to vectorize the sequence of ordered pairs

> data := seq([n,n^2/(3-n^2)], n = 0..10);

> plot([data], style=point, symbol=circle);

Next we show how Maple can be used for series. Maple provides a very powerful way to find Taylor series expansions, which you may recall can be very computationally intensive. Let us show a couple of examples. We begin with the Maclaurin series expansion of the function sin(2x).

> series(sin(2*x), x = 0, 10); This produces 10 terms in the series expansion.

This next example shows the Taylor series expansion for exp(-x²) about x = 2.

> series(exp(-x^2), x = 2, 5); This produces 5 terms in this series expansion.

Related to the series command is the sum command, which can be used to produce series and add finite and infinite series.

> sum(1/x^n, n = 1..10);

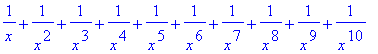
> sum(1/n^2, n = 1..infinity);

One can combine Maple commands such as the one below, which creates the sequence of partial sums for the alternating series

> Sum((-1)^i/i, i = 1..infinity); Note that the use of the capital letter at the beginning simply prints out the desired series.

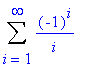
> seq(sum((-1)^i/i, i = 1..n), n=1..10);

Maple is capable of summing many of these series or letting you know that a series diverges.

> sum((-1)^n/n, n = 1..infinity);

Fourier Series

Maple gives a very quick way to compute Fourier series and visualize them. Many of the details can be found in the text in Chapter 10, p. 107. Fourier series often arise in the solution of partial differential equations using the separation of variables technique. Simply put, a Fourier series allows any periodic function to be represented by an infinite series of trigonometric functions.

The Fourier series of a function f(x) with period p = 2L is given by

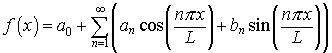
with

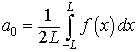
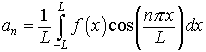
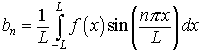
Note that even functions have only the a_n terms, while odd functions have only the b_n terms.

Suppose we want to represent the function, which is defined by

and has period 2 (repeating this line segment every 2 units along the x -axis), by a Fourier series. First we graph this function in Maple.

> f := piecewise(x < -1, x+2, x < 1, x, x < 3, x-2);

> plot(f, x = -3..3, discont=true);

This is an odd function, so it only has a sine Fourier series. The Fourier coefficients are given by

> bn := Int(x*sin(n*Pi*x), x = -1..1);

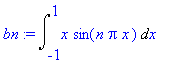
Maple readily does the integrals, then we can list say the first 8 of them.

> bn := int(x*sin(n*Pi*x), x = -1..1);

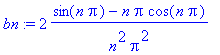
> seq(bn, n=1..8);

Maple has the ability to overlay different plots that you have produced with its plots package, using the display option. This is especially important if you want to view two different styles of plots, such as one with continuous lines and one with data points. below we graph the original function, then show this graph with Fourier approximations to the function with 1, 2, 5, and 20 sine functions. (In the limit as you add infinitely many Fourier approximating functions with the coefficients given above, the series converges pointwise to each point of the function where it is continuous and the midpoint between points where there are jump discontinuities.

> with(plots):

Warning, the name changecoords has been redefined

> F := plot(f, x = -3..3, discont=true, color=black):

> S1 := sum(bn*sin(n*Pi*x), n = 1..1);

> S2 := sum(bn*sin(n*Pi*x), n = 1..2);

> S5 := sum(bn*sin(n*Pi*x), n = 1..5):

> S20 := sum(bn*sin(n*Pi*x), n = 1..20):

> Fplot := plot({S1,S2,S5,S20}, x = -3..3):

> display({F,Fplot});