Example 1: Newton's Method applied to a quartic equation

1. Consider the function

f(x) = 4 + 8x² - x⁴.

a. Find the derivative of f(x) and the second derivative, f ''(x).

b. Find the y-intercept. Determine any maxima or minima and all points of inflection for f(x). Give both the x and y values.

c. Sketch the graph of f(x). Is this function odd or even or neither?

d. One of the x-intercepts is near x = 3. Use Newton's Method starting with x₀ = 3 and performing two iterations to get a good approximation to this x-intercept.

Solution:

a. The derivative can be found by the usual method,

b. At the y-intercept, x=0, so f(0) = 4 .

At the maxima and minima,

f '(x) = 0 = 16x - 4x³ = 4x(4 - x²) = 4x(2 - x) (2 +x)

The maxima and minima are therefore at x = 0, +2 .

f(2) = 4 + 8(2)² - (2)⁴ = 4 + 32 -16 = 20

so the maxima are at (2,20) and (-2,20) and the minimum is at (0,4)

Points of inflection can be found where

f''(x) = 0= 16 -12x² = 4(4-3 x²),

so and in this case, f(x) = 4 + 8(4/3) - (4/3)² = 116/9.

c.

 

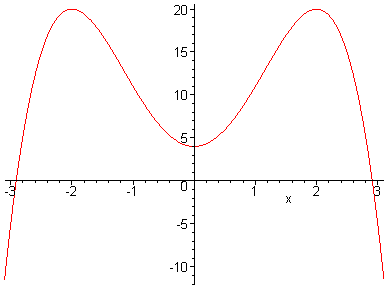
This is an even function, because it is a mirror image across the y-axis.

d. We begin at point x₀ = 3, and then we can find

f(3) = 4 + 8(3)² - (3)⁴ = -5

We also find

f '(x) = 16(3) - 4(3)³ = -60

The first Newton iterate is therefore

x₁ = 3 -(-5)/(-60) = 3 - 1/12 = 35/12 = 2.917

Using this value of x, we find f(x₁) and f '(x₁)

f(35/12) = 4 + 8(35/12)² - (35/12)⁴ = -.3125

and

f '(35/12) = 16(35/12) - 4(35/12)³ = -52.58

The second iterate is therefore

x₂ = 35/12 -(-.3125)/(-52.58) = 2.9107

To check our solution, if we substitute a = x² into this equation, f(a) = 4 + 8a - a²

then we can use the quadratic equation to find so a = 4 + 4.472

The solutions for x as the square root of a are therefore +2.9107.

Example 2: Newton's Method applied to a cubic equation

Consider the function

f(x) = x³ - 3x - 3.

a. Find all extrema and points of inflection, giving both the x and y values.

b. Is this function odd, even or neither? Sketch a graph of this function.

c. Use Newton's Method to approximate the value of the x-intercept. Start with x₀ = 2 and perform two iterations.

Solution:

a. The derivative can be found by the usual method, in order to find the extrema

At the maxima and minima, f '(x) = 0 = 3(x² - 1) = 3(x+1)(x-1)

The maxima and minima are therefore at x = +1.

f(1) = (1)³ - 3(1) - 3 = -5, and f(-1) = (-1)³ - 3(-1) - 3 = -1,

so the maximum is at (-1,-1) and the minimum is at (1, -5)

Points of inflection can be found where f''(x) = 6x²= 0, so x =0 and f(0) = -3.

b. This function is neither even nor odd.

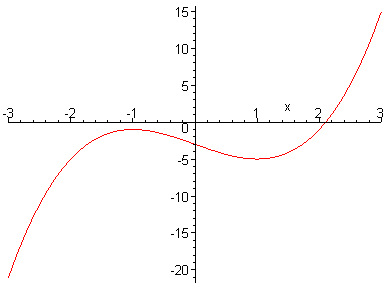
c. We begin at point x₀ = 2, and then we can find

f(2) = (2)³ - 3(2) - 3 = -1

We also find

f '(2) = 3(2)²-3 = 9

The first Newton iterate is therefore

x₁ = 2 -(-1)/(9) = 2 + 1/9 = 19/9 = 2.111

Now we find

f(19/9.) = (19/9)³ - 3(19/9) - 3 = .07545

We also find

f '(19/9) = 3(19/9)²-3 = 10.3704

The second Newton iterate is therefore

x₂ = 2.111 - (.07545/ 10.3704) = 2.1038

Example 3: Newton's Method applied to a cubic equation

3. Let

f(x) = 4 ln(x) - x.

a. Differentiate f and find any critical points. Determine the domain of f and sketch the graph.

b. Use Newton's Method to approximate the value of the x-intercept. Start with x₀ = 1 and perform two iterations to give the approximation of one zero. Then let x₀ = 8 and find x₁ to approximate the other zero.

Solution:

a. The derivative of f is

f '(x) = 4/x - 1.

The only critical point is when

4/x - 1 = 0,

so x = 4. It follows that there is a maximum at (4, 4 ln(4) - 4) = (4, 1.5452). The domain is x > 0.

b. The Newton's formula is given by

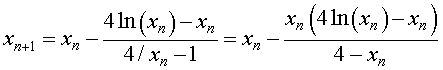
It follows that when x₀ = 1,

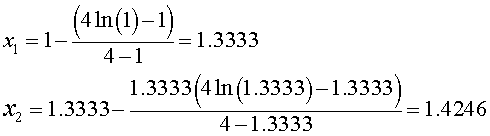
The actual intercept is x = 1.4296.

The other intercept is found by starting at x₀ = 8. The first Newton iterate is

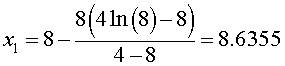
The actual intercept is x = 8.6132.