1. Improper Integral

This appendix is designed to introduce the Improper Integral. For sake of brevity, this appendix only handles the case where one of the limits of integration is infinity. The other type of improper integral is one where the function in the integrand goes to infinity. (Recall that in the Fundamental Theorem of Calculus, we imposed the condition that the function being integrated be continuous. This condition can be relaxed, but the function cannot go to infinity.)

Improper Integral

The Fundamental Theorem of Calculus requires that the limits of integration and the function being integrated be well-defined. There are many interesting cases the integral being considered needs to be evaluated with one or both of its limits of integration being infinity. In probability theory, the distribution function is defined to be the integral of the density function from minus infinity to some value x. Below we define an improper integral with its upper limit being infinity.

Definition: Let F(x) be any antiderivative of the continuous function f(x). The Improper Integral of f(x) with its upper limit being infinity is evaluated in the following manner:

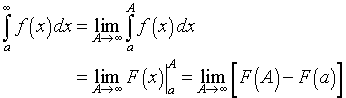
This integral is defined provided the limit

exists.

Example 1: Decaying Exponential

Consider the following improper integral that arises in applications where the data decays exponentially.

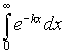
Solution: From the definition above, we can readily evaluate this integral as follows:

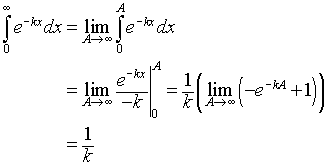
since

Example 2: Area and Volume of Infinite Object

When one considers infinite geometric objects, it is possible to have results that are counter-intuitive. In this problem, we examine the area under the curve f(x) = 1/x, from x = 1 to infinity, then consider the volume of the solid formed by rotating this curve about the x-axis on the same interval. The area under the curve is found by evaluating the integral

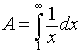
while the volume is found by evaluating the integral

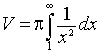
(Note that the volume is the area of the circle (p/x²) found by rotating curve about the x-axis times dx, which is integrated along the entire interval of interest.)

Solution: We begin with the improper integral representing the area. Below is a graph of this region.

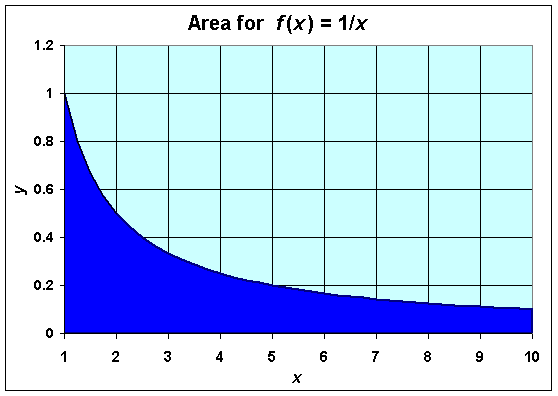
The integral is solved as follows:

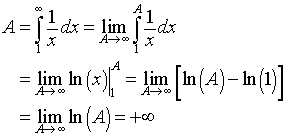
Thus, this limit does not exist. The region has an infinite area.

Next we examine the volume of the solid enclosed by rotating the curve above about the x-axis. This surface is shown below.

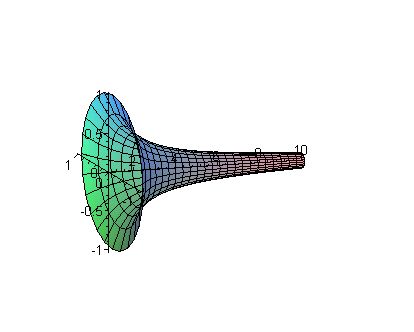
The integral is solved as follows:

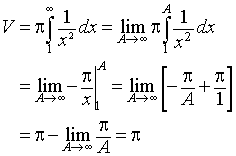
It follows that the volume of this solid is finite, in fact, equal to p. We are left with the following interesting scenario to consider. The volume of the solid of rotation is finite, so a finite quantity of paint can fill this solid. However, the cross-section of the region has infinite area, so you could never cover the region with paint. Think about this apparent paradox!