Math 121 - Calculus for Biology I
Spring Semester, 2004
Derivative of ex and ln(x)
San Diego State University -- This page last updated 02-Jan-04
|
|
Math 121 - Calculus for Biology I |
|
|---|---|---|
|
|
San Diego State University -- This page last updated 02-Jan-04 |
|
Fluoxetine, more commonly known by its trade name Prozac, is a selective serotonin reuptake inhibitor (SSRI). This drug is used to treat depression, obsessive compulsive disorder, and a number of other neurological disorders. It works by preventing serotonin from being reabsorbed too rapidly from the synapses between nerve cells, prolonging its availablity, which improves the patient's mood. Fluoxetine is metabolized in the liver and transformed into a slightly less potent SSRI, norfluoxetine. Both compounds bind to plasma protein, then become concentrated in the brain (up to 50 times more concentrated). Fluoxetine and norfluoxetine are eliminated from the brain with characteristic half-lives of 1-4 days and 7-15 days, respectively.
When performing studies of drugs, it is very important to understand the kinetics of the drug in the body. When the drug is metabolized into another active form, then the modeling becomes more complex. However, understanding how the body handles a drug is crucial to providing therapeutic levels of a drug and not allowing the drug's levels to become too elevated in the body. A number of first order kinetic models have been developed, and we will examine some equations that describe the concentrations of fluoxetine (F(t)) and norfluoxetine (N(t)) in the blood.
We begin this study with a discussion of the half-life of a drug. (This argument carries over to the half-life of radioactive material also.) Consider a subject taking a 40 mg oral dose of fluoxetine, which is rapidly taken into the blood stream to a concentration of 21 ng/ml. As reported in a study with healthy volunteers [1], the half-life of fluoxetine was 1.5 days. If we assume instantaneous uptake of the drug (which actually takes several hours), then we have the initial blood concentration of fluoxetine given by
F(0) = 21 ng/ml.
When a drug is either filtered out by the kidneys or metabolized by some organ such as the liver proportional to its concentration, then the drug is said to exhibit first-order kinetics and it decays exponentially with a characteristic half-life. Fluoxetine is metabolized in both the brain and liver, so satisfies the kinetic equation
F(t) = 21e-kt.
With a half-life of 1.5 days, we have
F(1.5) = 10.5 = 21e-1.5k.
Solving this equation for k, we have
e1.5k = 2
k = ln(2)/1.5 = 0.462.
Thus, a good model for blood plasma concentration of fluoxetine following a 40 mg oral dose is given by
F(t) = 21e-0.462t.
Fluoxetine is metabolized in the liver and through a hepatic biotransformation becomes norfluoxetine (through a demethylation). Norfluoxetine continues to act as potent and specific serotonin reuptake inhibitor, but has the added advantage of lasting much longer. (Some researchers believe that this is the primary therapeutic form of the drug because of its long persistence in the brain compared to fluoxetine.) Using the data from the Sunnybrook website [1] and taking the half-life to be 9 days for norfluoxetine, a reasonable model using linear kinetics for the blood plasma concentration of norfluoxetine is given by the equation
N(t) = 27.5(e-0.077t - e-0.462t).
(Note that all data from the Sunnybrook website [1] cannot be fit to a linear kinetic model, so this model chooses the peak value and half-life to be consistent.)
Below we show a graph of the fluoxetine and norfluoxetine concentrations from the models above. The graph supports the findings of some researchers that norfluoxetine provides much of the therapeutic dose of Prozac.
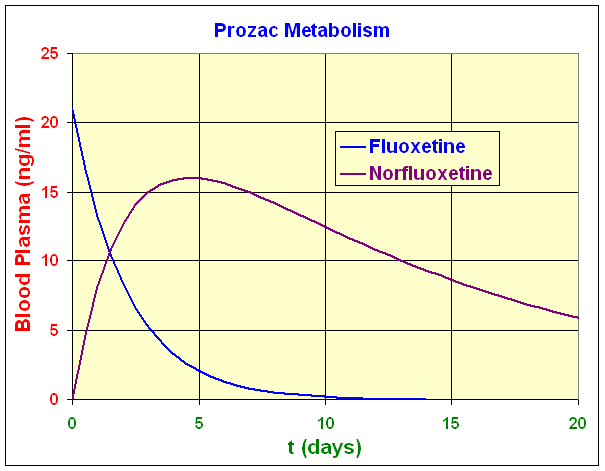
We want to use our techniques from Calculus to determine the rate of change of fluoxetine and to find the time of maximum blood plasma concentration of norfluoxetine and what that concentration is. To solve these problems, we need to learn the formula for the derivative of the exponential function.
Derivative of ekx
The exponential function ex is considered a special function. It is the only function (up to a scalar multiple) that is the derivative of itself. That is
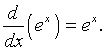
Note that by our scalar multiplication rule, then the derivative of f(x) = kex is f '(x) = kex.
From the definition of the derivative and using the properties of exponentials, we see that
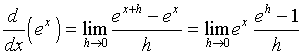 .
.One definition of the number e is the number that makes
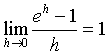
Geometrically, the function ex is a number raised to the power x, whose slope of the tangent line at x = 0 is 1.
The derivative of ekx is given by
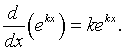
Example 1: Find the derivative of
Solution: From our rule of differentiation and the formula above, we have
Application of the Derivative to the Prozac Kinetic Model
We will use the derivative of the exponential function to find the rate of change of fluoxetine and norfluoxetine at various times, then find when the maximum concentration of norfluoxetine occurs and what that concentration is. We begin by finding the derivatives of the functions modeling blood plasma concentration of fluoxetine and norfluoxetine. From above, we have the concentration of fluoxetine is
F(t) = 21e-0.462t,
so the derivative is given by
F '(t) = (-0.462)21e-0.462t = -9.702e-0.462t.
Similarly for the blood plasma concentration of norfluoxetine
N(t) = 27.5e-0.077t - 27.5 e-0.462t,
so its derivative is
N '(t) = (-0.077)27.5e-0.077t - (-0.462)27.5 e-0.462t
= 12.705e-0.462t - 2.1175 e-0.077t.
If we want the rate of change of blood plasma concentrations of these two compounds at times t = 2 and 10, then we evaluate the rate of change of fluoxetine blood plasma concentration as
F '(2) = -9.702e-0.462(2) = -3.85 ng/ml/day,
F '(10) = -9.702e-0.462(10) = -0.0956 ng/ml/day.
Similarly, the rate of change of norfluoxetine blood plasma concentration is
N '(2) = 12.705e-0.462(2) - 2.1175 e-0.077(2) = 3.23 ng/ml/day,
N '(10) = 12.705e-0.462(10) - 2.1175 e-0.077(10) = -0.855 ng/ml/day.
These calculations show that at t = 2 the blood plasma concentration of fluoxetine is dropping quite rapidly, while blood plasm concentration of norfluoxetine is rising at a similar rate. The calculations at t = 10 show that the blood plasma concentration of both compounds are falling at fairly slow rates.
Maximum Concentration of Norfluoxetine
The maximum concentration of norfluoxetine is found by determining when the derivative is equal to zero. Thus,
N '(t) = 12.705e-0.462t - 2.1175 e-0.077t = 0
or
2.1175 e-0.077t = 12.705e-0.462t .
This gives
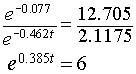
It follows that the maximum occurs at
0.385t = ln(6)
tmax = 4.654 days.
The maximum blood plasma concentration of norfluoxetine (as seen on the graph) is
N(tmax) =16.01 ng/ml.
Height and Weight Relationship for Children
The average height and weight of girls is given in the table below.
|
age(years)
|
height(cm)
|
weight(kg)
|
|
5
|
108
|
18.2
|
|
6
|
114
|
20.0
|
|
7
|
121
|
21.8
|
|
8
|
126
|
25.0
|
|
9
|
132
|
29.1
|
|
10
|
138
|
32.7
|
|
11
|
144
|
37.3
|
|
12
|
151
|
41.4
|
|
13
|
156
|
46.8
|
Ehrenberg noted that there was a logarithmic relationship between the height and the weight of children. Below is a graph of the data above, showing the height as a function of weight of girls ages 5 through 13 using data on the average height and weight of girls in the U. S.
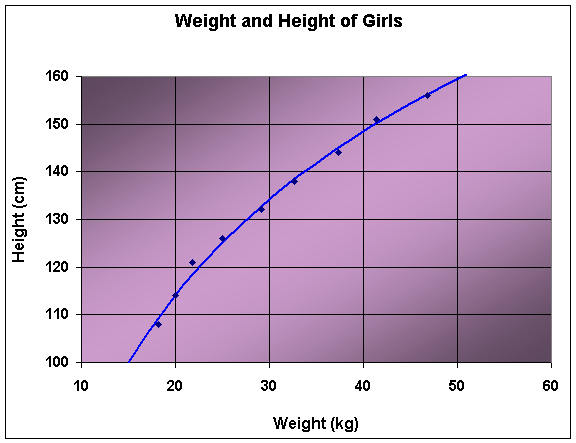
The formula for the height, H, as a function of weight, w, is given by
H(w) = 49.5ln(w) - 34.14.
We would like to find the find the rate of change of height with respect to weight for the average girl.
We cannot easily use the definition of the derivative to find the derivative of the natural logarithm. The derivative of the natural logarithm, ln(x), is given by the formula
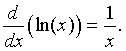
This relationship is most easily demonstrated after learning the Fundamental Theorem of Calculus in Math 122, which centers about the integral.
Derivative of the Height and Weight Relationship for Children
The relationship given above is easily differentiated with respect to w, using the derivative for the natural logarithm. It follows that
![]()
From this relationship, it is clear that as the weight increases, the rate of change in height decreases. For example, we can see that at a weight of 20 kg.
H '(20) = 49.5/20 = 2.475 cm/kg,
while at a weight of 49.5 kg
H '(49.5) = 49.5/49.5 = 1 cm/kg.
Note that this is not the rate of change of the height as a function of the age, which we saw to be nearly linear in the first section of the lecture notes.
Example 2: Find the derivative of
Solution: From our properties of logarithms and the formula above, we have f(x) = ln(x2) = 2ln(x), so
f '(x) = 2/x.
There are a collection of Worked Examples to help you understand this material and aid with the homework problems.
[1] Nicole Lee, Sunnybrook and Women's College Health Sciences Centre's Drug Information Site, <http://www.icomm.ca/shsc/kinetics/fluoxeti.html> 2075 Bayview Ave North York, Ontario M4N 3M5 CANADA