Math 121 - Calculus for Biology I
Spring Semester, 2011
Derivative of ex and ln(x) - Examples
San Diego State University -- This page last updated 03-Apr-11
|
|
Math 121 - Calculus for Biology I |
|
|---|---|---|
|
|
San Diego State University -- This page last updated 03-Apr-11 |
|
The examples below explore more differentiation of the exponential and logarithm functions, including the graphs of these functions. There are examples of a polymer drug delivery device, radioactive decay, and the growth of fish with the von Bertalanffy equation.
Example 1: Find the derivatives of the following functions:
Solution: We begin with the derivative of f(x). The rules of differentiation give
For g(x), we first use the properties of logarithms to change the expression so that it only includes ln(x)
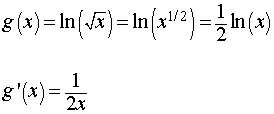
Graphing Exponential and Logarithms
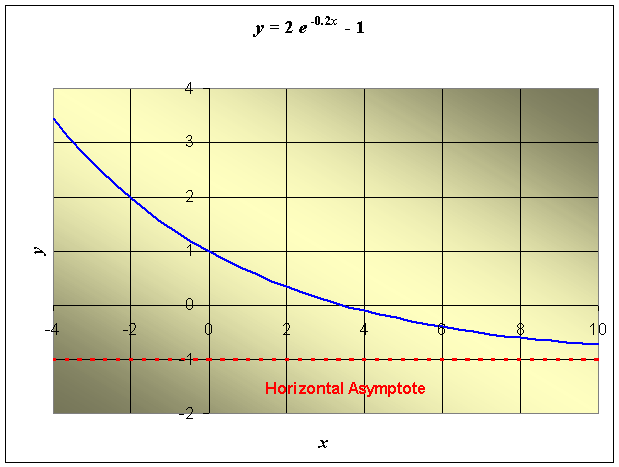
Example 2: Consider the following function
y = 2e-0.2x - 1.
Graph this function and find its derivative.
Solution: The domain of this function is all values of x. The y-intercept satisfies
2e-0.2(0) - 1 = 1.
The x-intercept satisfies
2e-0.2x - 1 = 0
2e-0.2x = 1
e0.2x = 2
x = 5 ln(2) = 3.466
For large values of x, the exponential function decays to zero. Thus, there is a horizontal asymptote to the right with
y = -1.
Often when there is an exponential function, there is a horizontal asymptote going either to the right (negative constant times x) or to the left (positive constant times x).
The graph of the function is given by
The derivative of this function satisfies
y' = 2(-0.2) e-0.2x = -0.4 e-0.2x.
Since the exponential function is always positive, the derivative is always negative though the derivative does approach zero as x becomes large (approaching the horizontal asymptote). Thus, this function is always decreasing, which is clearly shown in the graph.
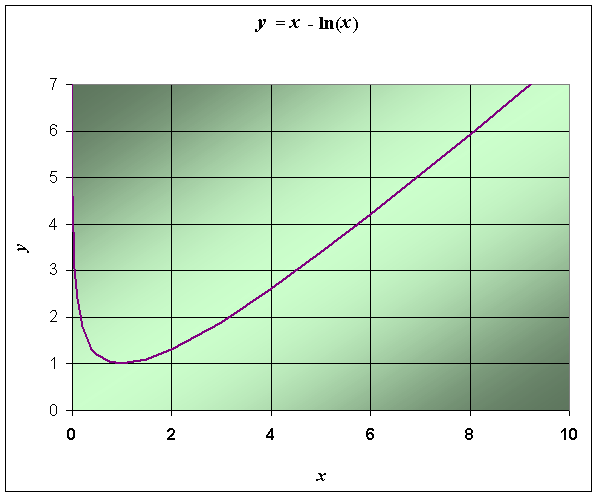
Example 3: Consider the following function
y = x - ln(x) .
Find the first and second derivatives of this function. Find any local extrema, then graph the function.
Solution: The derivative for this function is given by
![]()
The second derivative is given by
![]()
Graphing the Function:
This function is only defined for x > 0. Thus, there is no y-intercept. However, there is a vertical asymptote at x = 0.
We find extrema by setting the derivative equal to zero. The derivative is zero only when the numerator of the above expression for the derivative is zero, so x = 1. This gives an extremum at (1, 1).
Since the second derivative is always positive, which says that this function is concave upwards. It follows that the extremum computed above is a minimum.
The graph of the function is given by
Example 4: Polymer Drug Delivery System
This problem compares drug concentration in the body following an injection and compares this to the new polymer drug delivery devices. Drugs have long been administered by either a pill or an injection. The result is that the body receives a fairly high dose rapidly, then the drug remaining in the blood disappears in an exponentially decaying manner. Recently, scientists have invented polymers that can be implanted to deliver a drug or hormone for a much longer period of time. For example, there are several long term birth control devices that are injected just below the skin. These devices deliver the hormones estrogen and progesterone at sufficiently high levels for extended periods of time to prevent pregnancy. These new drug delivery devices are a hot area of research for a variety of medical conditions. These devices could aid diabetes sufferers with a more uniform level of insulin or they could deliver chemotherapeutic drugs to cancer patients over a much longer period of time at lower doses to maximize their efficacy.
We want to study equal quantities of drug delivered by an injection and by a polymer drug delivery device. When a drug is delivered by an injection, the drug is cleared relatively rapidly by either filtration of the kidneys or metabolism. The concentration in the blood is given by the formula
k(t) = A0e-qt,
where A0 and q are constants representing the amount of drug injected and the rate that the drug is cleared from the body. When the same drug is delivered by a polymer delivery device, then it is typically described by two decaying exponentials. This system is given by the model
where c(t) is the concentration of the drug and C0, r, and q are constants depending on the drug delivery system with q > r. C0 is a constant that indicates the level of the drug or hormone trapped in the polymer delivery device. The kinetic constants r and q are associated with the decay of the polymer that releases the drug and the degradation of the drug in the body of the patient, respectively. For the amounts of drug to be the same, then
A0 = C0/r.
Consider a specific example where the injected drug satisfies
k(t) = 1000e-0.2t,
where the k(t) is a concentration in mg/dl and the time t is in days. The same amount of drug is delivered by a polymer drug delivery device and is given by
where the c(t) is a concentration in mg/dl.
Find the rate of change in concentration for both k(t) and c(t) at t = 5 and 20. Also, determine the maximum concentration of c(t) and when it occurs. Graph each of these functions.
Solution: We begin by finding the derivatives of k(t) and c(t). Using the rule of differentiation for exponentials, we find that
k '(t) = (-0.2)1000e-0.2t = -200e-0.2t
and
c'(t) = 10 (-0.01e-0.01t - (-0.2)e-0.2t) = 2 e-0.2t - 0.1 e-0.01t.
If we want the rate of change of the drug concentrations at times t = 5 and 20, then the injected drug gives declining rates of change
k '(5) = -200 e-0.2(5) = -73.58 mg/dl/day,
k '(20) = -200 e-0.2(20) = -3.66 mg/dl/day.
Similarly, the rate of change of the polymer delivered drug is
c '(5) = 2 e-0.2(5) - 0.1 e-0.01(5) = 0.64 mg/dl/day,
c '(20) = 2 e-0.2(20) - 0.1 e-0.01(20) = -0.045 mg/dl/day.
The maximum is found by taking the derivative of c(t) and setting it equal to zero. From the derivative above, we have
0.1 e-0.01t = 2 e-0.2t
e-0.01t + 0.2t = 20
e0.19t = 20.
Thus, t = ln(20)/0.19 = 15.767 days. The maximum occurs at c(15.767) = 8.11 mg/dl.
Below we graph the two functions, k(t) and c(t).
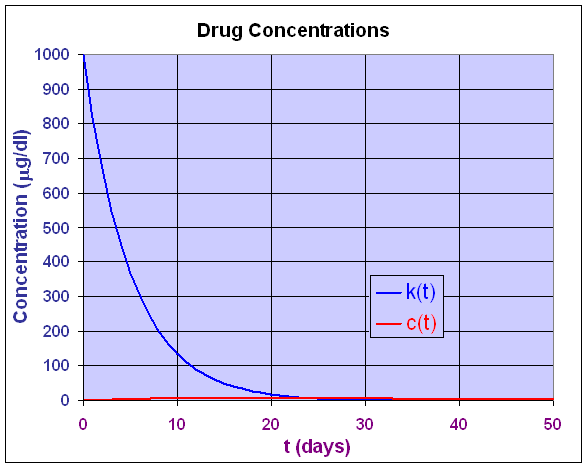
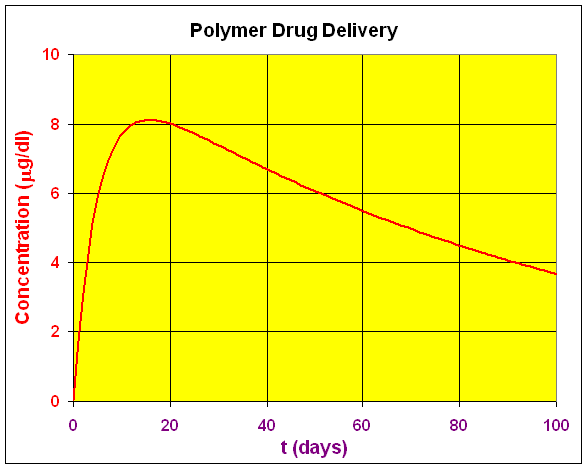
This graph shows the large amount from the injection, which decays very rapidly. By setting the two concentrations equal to each other, we can readily find that the functions are equal when t = 24.29 days with concentrations of 7.766 mg/dl. The injected drug falls off very rapidly, continuing its decline, while the polymer delivered drug maintains a relatively constant level over a much longer time. Below we show just the graph of the polymer delivered drug over a longer period of time. Its maximum concentration is easily seen in the graph. The graph above shows the obvious advantages of the time released drug if it has serious side effects or toxicity.
Example 5: Naturally-occurring potassium is not radioactive, but radioactive isotopes can be manufactured from natural potassium. Potassium isotope 43 decays at a rate proportional to the amount of the radioactive potassium available. After it emits a beta ray, it reverts to calcium. (43K goes through a b- decay with a neutron changing to a proton to produce 43Ca.) This can be used as a tracer for studying the effectiveness of potassium absorption in the body.
Suppose we begin with a 10 mCi (millicurie) sample of 43K. This substance has a half-life of 22 hours. Find the amount of 43K after 5, 20, and 50 hours. Also, find the rate of loss of 43K after 5, 20, and 50 hours.
Solution: If a radioactive substance has a half-life of x hours, then it decays exponentially to half its original amount in x hours. Let K(t) be the amount of 43K, then an expression for the amount of 43K is given by
where the constant k must be determined based on the half-life. If the amount of K(t) drops to 5 mg in 22 hours, then we know that
K(22) = 5 = 10e-22k
e-22k = 1/2
e22k = 2.
By taking the natural log of both sides, we see that
Thus, we can write the expression for K(t) as
With this expression for K(t), we can readily find the amount of 43K after 5, 20, and 50 hours. We have
K(5) = 10e-5k ~ 10 e-0.1575 ~ 8.54 mCi,
K(20) = 10e-20k ~ 10 e-0.6301 ~ 5.325 mCi,
K(50) = 10e-50k ~ 10 e-1.575 ~ 2.07 mCi.
To find the rate of change in the amount of K(t) at a given time, we need the derivative of K(t). From the rule for differentiating the exponential function, we have
With this expression for K '(t), we can readily find the rate of change in the amount of 43K after 5, 20, and 50 hours. We have
K '(5) = -10ke-5k ~ -0.315 e-0.1575 ~ -0.269 mCi/h,
K '(5) = -10ke-20k ~ -0.315 e-0.6301 ~ -0.168 mCi/h,
K '(5) = -10ke-50k ~ -0.315 e-1.575 ~ -0.0652 mCi/h.
This gives an estimate at each time of how much beta radiation is coming from the sample of 43K.
Example 6 (von Bertalanffy Equation): As a fish ages, it reaches a maximum size. A model for fish growth was developed by von Bertalanffy, which has an exponential solution.
a. Data shows that on average a lake trout takes 5.5 years to reach 2 kg and 15 years to reach 5 kg. When these data are fit to the von Bertalanffy equation, an equation for weight as a function of age is given by
W(a) = 20.2(1 - e-0.019a).
Find the rate of change of weight, W, with respect to the age, a. Graph the solution of the von Bertalanffy equation showing the intercepts and any asymptotes.
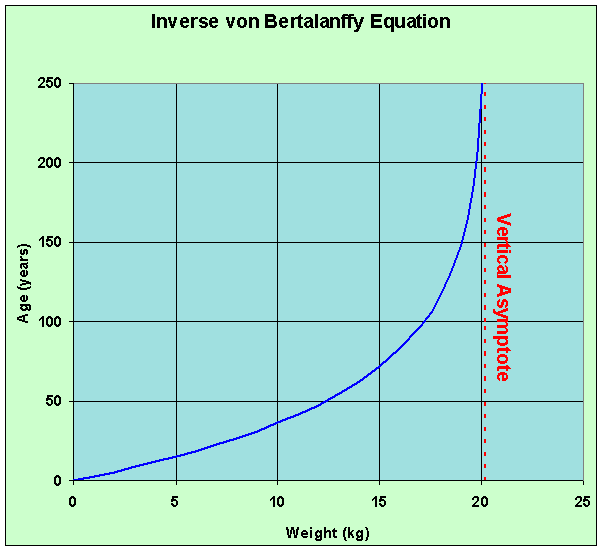
b. Solve the above equation for age, a, as a function of the weight, W. Differentiate this function, finding the rate of change of age with respect to weight. Graph this function showing any intercepts and asymptotes.
Solution: a. Write the von Bertalanffy equation as follows,
W(a) = 20.2 - 20.2 e-0.019a
then differentiating with respect to the age, a, gives
![]()
This says that the function is monotonically increasing (as we would expect for growth of a fish).
This equation goes through the origin, and it is easy to see that for large values of a the exponential decays to zero, which implies that asymptotically the fish grows to a weight of 20.2 kg. This is the horizontal asymptote. Below is a graph of the von Bertalanffy equation

b. Next solve the equation
W = 20.2 - 20.2 e-0.019a
for the age, a. It follows that
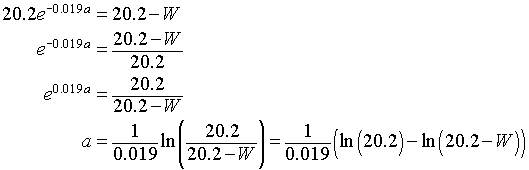
Thus, we can write the age, a, as a function of the weight, W. It is given by
a(W) = 158.2 - 52.63 ln(20.2 - W).
Unfortunately, this expression cannot be directly differentiated without the chain rule (to be learned soon). However, try a substitution of Z = 20.2 - W. (Note that dZ/dW = -1, which is just a sign change.) With this substitution, we have
a(Z) = 158.2 - 52.63 ln(Z),
and
![]()
We will find with the chain rule that
![]()
Since Z = 20.2 - W and dZ/dW = -1, the formula gives
![]()
The graph of the inverse function for the von Bertalanffy equation given by a(W) has a domain of W < 20.2. There is a vertical asymptote at W = 20.2. The derivative above shows that this function is strictly increasing. Since the function W(a) passes through the origin, its inverse function also passes through the origin
a(0) = 158.2 - 52.63 ln(20.2) = 0.
Below is the graph of this inverse function.