Math 336 - Mathematical Modeling Spring Semester, 2000
	© 1999, All Rights Reserved, SDSU & Joseph M. Mahaffy San Diego State University -- This page last updated 1-Feb-00

  Outline of Chapter

1. Chirping Crickets and Temperature
2. Juvenile Height
3. References
4. Problems

Chirping Crickets and Temperature

For many years people have recognized a relationship between the temperature and the rate at which crickets are chirping. The folk method of determining the temperature in degrees Fahrenheit is to count the number of chirps in a minute and divide by 4, then add 40. In 1898, A. E. Dolbear [3] noted that "crickets in a field [chirp] synchronously, keeping time as if led by the wand of a conductor." In his paper, he appears to be the first person to write down a formula in a scientific publication, giving a linear relationship for the temperature based on the chirp rate of crickets. The mathematical formula that he gave is:

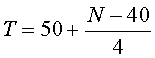
Does this formula of Dolbear match the folk method described above?

Many of the early papers [1,2] begin with the authors' fond memories of listening to snowy tree crickets, Oecanthulus niveus, in the late summer and early fall, then they dispute how synchronized the actual chirping is. However, the mathematical models are all very similar.

Below is the data from C. A. Bessey and E. A. Bessey on eight different crickets that they observed in Lincoln, Nebraska during August and September, 1897. It is apparent from these data that a fairly good estimate of the temperature is found by drawing a straight line through the points. A Java applet is provided so that you can adjust the coefficients of the straight line. Change the coefficients of the equation of the line below until you see a line that looks to you as if it fits the data. This line would be a good model for finding the temperature outside based on the rate at which the crickets are chirping.

The line given by the Bessey brothers is the least squares best fit to the data they collected. (The actual formula that they presented is T = 60 + (N - 92)/4.7, which you can check reduces to the formula stated in the graph above.) We will examine what a least squares best fit means in the next section.

Dolbear's Cricket Equation as a Linear Model

The line that you found passing through the data creates a mathematical model for representing the temperature as a function of the rate at which snowy tree crickets chirp. Before studying this model for mathematical properties, we should ask a few questions about the biological model.

1. How well does the line that you found fitting the Bessey & Bessey data agree with the Dolbear model given above?
2. When can this model be applied from a practical perspective?
3. Over what range of temperatures is this model valid?
4. How accurate is the model and how might the accuracy be improved?

The answers to these questions should help you appreciate the complex relationship between the biology of the problem and the mathematical model. The answers that are given below are not complete, but should help you appreciate how one approaches mathematical modeling and a biological problem. Hopefully, this will give you a better appreciation of how mathematics is used and some of its limitations.

The first two questions are actually very biological in nature, and the mathematics play a very limited role. The comparison of the Dolbear formula to the linear model shows some discrepancies in the coefficients of the linear model. However, you should be asking the biological question about the organisms that were being studied. The differences in the mathematical formulae may very well be due to observations made on different species of crickets. However, if you believe that the two different observations are similar, then this model may be a good biological thermometer. From a practical perspective, this biological thermometer has limited use. The snowy tree crickets only chirp for a couple months of the year. Furthermore, they only tend to chirp at night when the temperature is above 50^oF.

The last two questions provide important links between the process of mathematical modeling and the biological problem being studied. The range of validity in temperatures for the model gives the domain where we can use this model. Generally, you should limit the use of the mathematical model to points between the range where the data are collected (or possibly to intervals that are only slightly beyond the collected data points). For our cricket thermometer equation, we see that the data only allows its use between 50^oF and 85^oF. However, this temperature range is appropriate for evenings in Nebraska in August and September, which is where this particular thermometer is valid. Statistical analysis of the data will help provide the degree of accuracy of the mathematical model, but it appears that our model will probably give the temperature within a couple degrees Fahrenheit. The folk formula is less accurate than the model formed by data, but it is much more easily applied. So which technique are you more likely to use on a warm summer night talking to some friends?

You created a model above by adjusting the slope and intercept of a linear equation until you saw a model that looks good. Mathematically, we often use a linear least squares fit to find the best fit to the data. These notes will provide more information on the technique of linear least squares, and later chapters will discuss more complicated models. The data could be better fit by a more complicated mathematical model, such as fitting a quadratic through the data. However, this may not be appropriate from either a biological or mathematical perspective, but that depends on the problem and is acquired through experience. The next section below will provide a review of straight lines and remind you of some important mathematical definitions.

Juvenile Height

In the table below we show average juvenile height as a function of age [4].

 The height, h, is graphed as a function of the age, a. The data from the table are shown below. It is easy to see that the data almost lie on a line, which suggests a linear model.

The Java applet allows you to adjust the coefficients of the linear model. Change the coefficients of the equation of the line above until the line, representing the height as a function of age, fits the data. This line would be a good model for finding the average height of a child for any age between one and thirteen.

The line that best fits the data above is given by

where m = 6.46 is the slope and b = 72.3 is the h-intercept. The next section will explain finding the linear least squares best fit or linear regression to the data.

From a modeling perspective, it is often valuable to place units on each of the coefficients or variables in the equation. In an equation the units must always match. The height, h, from our data has units of cm, so both ma and the intercept b must have units cm. Since the age, a, has units of years, it follows that the slope, m, has units of cm/year. From the units it is easy to see that the slope is the rate of growth. (This idea of rate of growth will occur regularly in this course!)

The line above gives a mathematical model for growth of the average child. With this mathematical model, what type of questions can you answer? See if you can answer the following questions.

1. What is the average height of an eight year old?
2. What height does the model predict for a newborn baby?
3. If a six year old child is 110cm, then estimate how old she'll be at age 7.

Answers: 1. The model predicts that the average eight year old will be 124 cm, which is found by setting a = 8 in the model.

2. The height intercept represents the height of a newborn., so this model predicts that a newborn would be 72.3 cm. However, this is outside the range of the data, which makes its value more suspect.

3. The model indicates that the growth rate is about 6.5 cm/year, so the six year old should grow about 6.5 cm and be 116.5 cm at age 7 though the average 7 year old as predicted by the model would be 117.5 cm.

What are some of the limitations and how might the model be improved?

The most obvious limitation is that this linear model would certainly not extend much beyond the ages listed in the table. (You would not predict the average 20 year old to be 201.5 cm as the model predicts.) Thus, the domain of this function is restricted to some interval around 1 < a < 13.

Let's examine the questions above to see if we might derive better estimates. A better prediction of average eight year olds would be to average the heights of seven and nine year olds (125.5 cm). This is known as a local analysis, meaning that approximating a function is always better by using nearby information. Similarly, we might improve our estimate on the length of a newborn by using only the data given for one and three year olds (66.5 cm). As we study Calculus more, we will see that its this local study of growth rates that is of greatest interest. The answer to the third question is about as good as we can do with the given information. If you had more data on the individual child, you might be able to predict her height better from her history than using the history of this average set of children.

There are several improvements you might want in a model like this. (Recall that models are only a window on the real world and usually can be improved.) The model is an average of juveniles indicating that the data have both sexes included, and our experience suggests that growth rates for girls and boys differ. Thus, you might want to split the data according to sex. Close inspection of the data shows that there is a faster growth rate between 0 and 5, and then again between 9 and 13, which agrees with the common idea that growth occurs in spurts. You might improve the model to include this information by using something other than a straight line to fit the data. However, you must consider how much is gained by a more complicated model. 

References

 [1] H. A. Allard, The chirping rates of the snowy tree cricket (Oecanthus niveus) as affected by external conditions, Canadian Entomologist (1930) 52, 131-142.

[2] C. A. Bessey and E. A. Bessey, Further notes on thermometer crickets, American Naturalist (1898) 32, 263-264.

[3] A. E. Dolbear, The cricket as a thermometer, American Naturalist (1897) 31, 970-971.

[4] David N. Holvey, editor, The Merck Manual of Diagnosis and Therapy (1987) 15^th ed., Merck Sharp & Dohme Research Laboratories, Rahway, NJ.

Problems

1. Most of the world uses the metric system. Convert the following scenario into one that someone from a metric based country could better understand. Its a beautiful morning with a temperature of 75^oF. We travel 5 miles to a beautiful place to take a dive. The water temperature is 65^oF with a breeze of 15 miles per hour. We swim 400 yards out to our dive spot where we submerge to a depth of 50 feet. Among the animals that we see are 5 inch abalone, 14 inch lobsters, 2 inch banded gobies, and a 4 foot leopard shark. At the end of the dive we surface 150 yards from shore in 15 feet of water. My tank gauge registers 700 psi (pounds per square inch) of air remaining. (Note that metric countries often use SCUBA gauges in kg/square cm.)

2. Convert this statement from someone in Canada into English units for someone in the United States. Its a beautiful day to go cross-country skiing as the temperature is -10^oC, so I packed a 4 kg pack, including 2 liters of water. I travelled 70 kilometers North to the Laurentians where the elevation is about 400 meters. The temperature in the mountains was perfect green wax conditions with -14^oC and a breeze of 25 km/hour. The trail traversed 17 km of maple forests with 40 cm diameter trees over an expanse of 30 km².

3. a. The lecture notes gave the average heights of five and seven year olds as 108 cm and 121 cm, respectively. Use these data to estimate the average height of a six year old. What is the average rate of growth for children these ages in cm/yr?

b. The lecture notes showed the average height of a child satisfies the equation:

h = 6.46 a + 72.3,

where h is the height and a in the age of the child. Find the average height of a six year old using this equation. Is this estimate better or worse than the estimate in Part a. and why?

c.Use the equation in Part b. for height of a child. If your daughter is 135 cm at age nine, then what does the model predict her height to be at age ten? If she is 160 cm at age 13, then what does the model predict her height to be at age 15? Which of these estimates is better and why?

4. A few years ago some Exercise Physiologists at UCLA published a paper in NATURE wherein they predicted that by the year 2004, the women's world record in the marathon would be faster than the men's record. The mechanism for the improvement in performance is thought to be the improvement of training methods and the expansion of the talent pool. But the data was examined only to describe the trend, not to explain it.

This problem examines the winning Olympic times for the 100 m races for both Men and Women. As the years have gone by, the times have improved for both Men and Women. Below we present a table with the data for the winning times (in seconds)

Year	Men's 100	time	Women's 100	time
1896	Burke	12.0
1900	Jarvis	11.0
1904	Hahn	11.0
1906	Hahn	11.2
1908	Walker	10.8
1912	Craig	10.8
1920	Paddock	10.8
1924	Abrahams	10.6
1928	Williams	10.8	Robinson	12.2
1932	Tolan	10.3	Walasiewicz	11.9
1936	Owens	10.3	Stephens	11.5
1948	Dillard	10.3	Blankers-Koen	11.9
1952	Remigino	10.4	Jackson	11.5
1956	Morrow	10.5	Cuthbert	11.5
1960	Har	10.2	Rudolph	11.0
1964	Hayes	10.0	Tyus	11.4
1968	Hines	9.95	Tyus	11.0
1972	Borsov	10.14	Stecher	11.07
1976	Crawford	10.06	Richter	11.08
1980	Wells	10.25	Kondratyeva	11.06
1984	Lewis	9.99	Ashford	10.97
1988	Lewis	9.92	Joyner	10.54
1992	Christie	9.96	Devers	10.82
1996	Bailey	9.84	Devers	10.94

a. Use EXCEL's trendline feature to find the best straight lines (one for Men and one for Women) through the data, where

is the straight line for the best time (T) as a function of the Olympic year (Y) with EXCEL determining the slope (m) and intercept (b). Write the equations for the best linear models and show (on a single graph) the graphs of the data and linear model for both Men and Women. Be sure to label which lines correspond to the data for the Men and Women.

b. Use the model to determine the predicted year when the best time is 10.0 sec for Men and 11.0 sec for Women, then compare your prediction to the actual data.

c. Use the model to predict the time for the 2000 Olympics for both Men and Women in this event.

d. According to the model, which Olympics will first see Women outrunning the Men? Give a short discussion on the validity of this prediction and why you think it is true or false. What fundamental premise do you consider to be critical? Can you formulate another model that might be more valid?