1. Distance for Seed Dispersal
2. Integration by Parts
3. Worked Examples
4. Mean Distance for the Dispersal of Seeds

This section examines a technique of integration known as integration by parts. It also introduces some concepts from probability theory for continuous distributions. These ideas are combined to allow the computation of the mean distance that a seed travels.

 Distance for Seed Dispersal

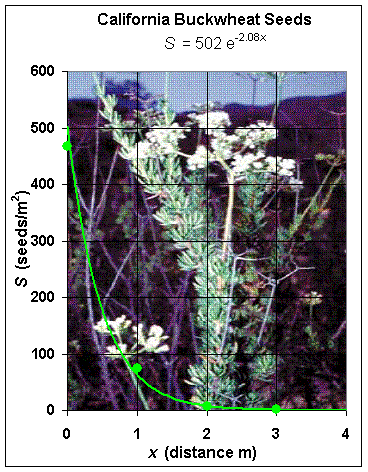
Plants have developed a number of methods for dispersing their seeds. Plants need to have their seeds carry a distance from the mother plant to avoid crowding and shading from the mother plant. One of the most common methods of seed dispersal is for the seeds to shoot from the plant or blow away by the wind. This results in an exponential distribution of seeds decaying as the distance from the mother plant increases. John Chalekian and Professor Doug Deutschman of San Diego State University ran a series of experiments to determine the distribution of seeds from a native plant in this region, California Buckwheat, Eriogonum fasciculatum. Below is a table and graph of from one of their sets of data showing the number of seeds/m² for one plant of Eriogonum fasciculatum.

E. fasciculatum Dist. (m) Seeds (#/m2) 0 467 1 74 2 7 3 1

The best fit to these data (as seen in the graph above) is the exponential decay function given by

S(x) = 502e^-2.08x.

One key application of integration comes from the field of probability and statistics. Many biological data fit standard density or distribution functions used in statistical analysis, such as the decaying exponential from the seed example above. Additional information on probability density functions and distribution functions is available in a hyperlink to a special section introducing ideas from probability. If the density function has been normalized so that the integral over the entire range of the probability density is one, then one can find the probability of some event happening on some interval in the range of the density function by integrating the function over that range. The exponential density function for our example above satisfies

f(x) = 2.08e^-2.08x.

If we use this function to find the probability of finding a seed between 1 and 2 meters from the plant, then we evaluate the following integral:

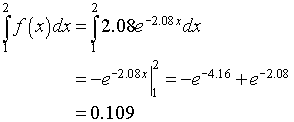
The data show that the fraction of seeds recovered over this range is 74/549 = 0.135, which is similar to the value computed by the integral. The table below shows the values computed from the data and the values computed by the integral

Another useful application that uses the probability density functions is known as the Expected value of the random variable X. You will learn much more about probability density and distribution functions, random variables, and expected value in the Bio 215 course on Statistics, but a quick summary can be found in the Special Probability Hyperlink provided here. Since the random variable in our exponential density function for the seed dispersal problem measures the distance from the mother plant, then the expected value gives the mean distance that the seeds for our example above have tranversed from the mother plant. The expected value for the mean distance that the seeds travel is given by the formula

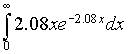
The integral involves x times an exponential function, which cannot be solved using the integration techniques that we have learned to this point in the course. The technique for solving this integral is called integration by parts.

Integration by Parts

Integration by parts is a technique that is based on the product rule of differentiation. The product rule of differentiation states that

 

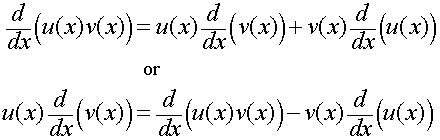
When the second equation is integrated, then we have the integration by parts formula:

Below we show how this formula helps solve several integration problems.

Examples: Each of the examples below need the technique of integration by parts.

1. Consider the integral given by:

For this problem we let u(x) = x and v'(x) = e^-2x. The expression for v'(x) can be easily integrated to give

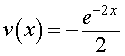
The choice of u(x) = x was made so that upon differentiation this expression became simpler. In particular, u'(x) = 1. Now we apply the integration by parts formula to see that

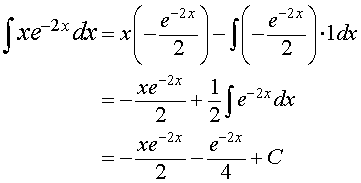
2. Now consider the integral given by:

For this problem we let u(x) = ln(x), which upon differentiation gives

We take v'(x) = 1. The expression for v'(x) can be easily integrated to give

Now we apply the integration by parts formula to see that

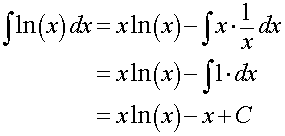
Mean Distance for the Dispersal of Seeds

We now return to the seed dispersal problem from above where we had a definite integral that needed to be solved using integration by parts. When you have a definite integral that is integrated by parts, you can apply the Fundamental Theorem of Calculus learned in the previous section to evaluate this integral. The integral for this problem is further complicated by the fact that it is an improper integral, since the upper limit of integration is infinity. A short appendix is given to show how these types of improper integrals are handled.

We can apply the results of what we have learned to evaluate the expected value for the mean distance that the seeds travel in the improper integral listed above. Below we detail the steps necessary to find this mean. In the integral, we let

u(x) = x and dv = 2.08e^-2.08xdx,

so

du =dx and v(x) = -e^-2.08x.

It follows that

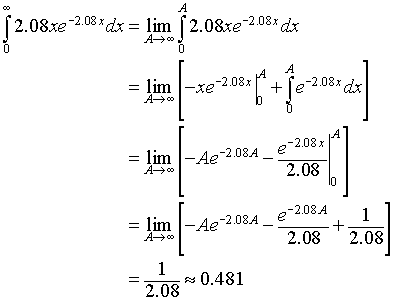
Thus, the mean distance that a seed travels for California Buckwheat, Eriogonum fasciculatum, is 0.481 m according to this experimental result.