1. Respiratory Dead Space
2. Fundamental Theorem of Calculus
3. Examples
4. Worked Examples
5. Volume of the Dead Space 

The previous section showed how to approximate the area under a curve using the Midpoint rule. However, this technique is rather tedious. This section uses our techniques from earlier sections with the antiderivative to find the area under a curve. The Fundamental Theorem of Calculus allows the use of the definite integral to find the exact area under a function. We illustrate the use of our integration techniques with an example from Respiration physiology.

Repiratory Dead Space

When breathing air in and out of the lungs, the air must pass through the nasal passageways, the pharnyx, the trachea, and the bronchi before it can enter the alveoli where the oxygen and carbon dioxide exchange with the circulatory system. These regions where vital gases cannot be exchanged are called dead spaces. To determine the health of patients with respiratory problems, it is important to know information on all aspects of their lungs. This includes the measurement of the dead space.

There is a fairly simple means of measuring the dead space for a patient. The patient breathes normal air, then just before the measurement, he or she takes a single breath of pure oxygen. The oxygen will mix with the normal air in the alveoli, but the dead space will be filled almost exclusively with pure oxygen. The patient expires the mixture through a rapidly recording nitrogen meter. The recording gives a measurement of the amount of N₂, and the part that includes only O₂ represents the dead space. Below is a graph showing a typical recording of a patient.

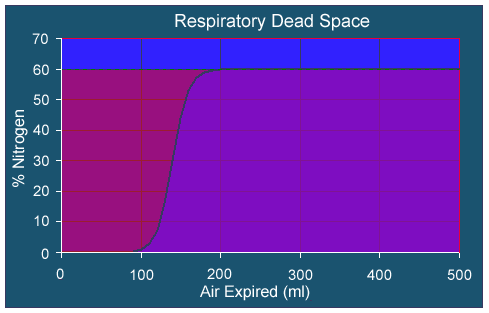
The region to the left of the curve is the pure O₂ in the dead space, while the region to the right of the curve represents the mixed air in the alevoli where that actual gas is being exchanged with the circulatory system. The volume of the dead space is given by the area to the left of the curve times the total volume of air expired divided by the total area under the dotted line.

A function that closely approximates the data collected above is given by

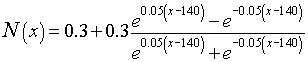
where N is the percent of nitrogen in the expired air and x is the number of milliliters expired. We can readily see that the total area (V) under the dotted line is V = 0.6x500 = 300 ml, so we can find the area to the left of the curve by finding the area under the curve and subtracting it from the total area, V. We would like an simpler means than the Riemann sums to find the area under this curve, and the Fundamental Theorem of Calculus gives us this tool. Below we complete our computation to arrive at the actual volume of the dead space represented by the data above.

The Fundamental Theorem of Calculus

Let f(x) be a continuous function on the interval [a,b] and assume that F(x) is any antiderivative of f(x). The definite integral, which gives the area under the curve f(x) between a and b, can be computed by the following formula:

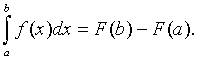
Example 1: Use the Fundamental Theorem of Calculus to evaluate the integral of f(x) = x² from 0 to 2.

Solution: The solution is given by

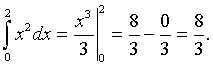
Note that this represents the area under the curve x² from 0 to 2.

Example 2: Consider the functions f(x) = x² - 2x - 3 and g(x) = 1 - 2x. Find the x and y-intercepts and the vertex of the parabola. Also, find the points of intersection. Finally, determine the area between the curves.

Solution: For f(x), the y-intercept is (0, -3). By factoring, f(x) = x² - 2x - 3 = (x - 3)(x + 1), so the x-intercepts are (-1, 0) and (3, 0). The vertex has its x value midway between the two x-intercepts, so it is easy to see that the vertex of this parabola is (1, -4). For the straight line g(x) = 1 - 2x, the x and y-intercepts are (1/2, 0) and (0, 1), respectively.

To find the points of intersection, the functions are set equal to each other. Thus, x² - 2x - 3 = 1 - 2x or x² - 4 = 0. The x values of intersection are x = +2, so the point of intersection are (-2, 5) and (2, -3). Below is a graph of the two curves showing the region between them.

 

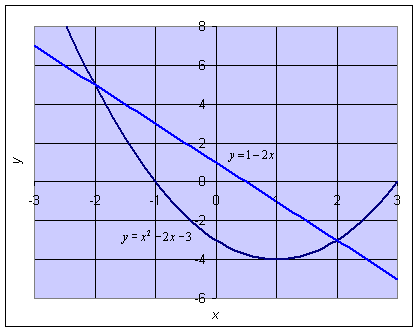
From the points of intersection, we see that the domain of interest is -2 < x < 2. Notice that g(x) > f(x) over the interval of interest, which gives the height at any x as g(x) - f(x) = (1 - 2x) - (x² - 2x - 3) = 4 - x². Thus, the area is found by the following integral

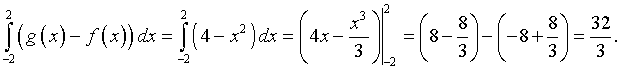
Example 3: When the integration requires substitution, then the substitution used in the integration can also be used on the endpoints of integration to simplify the process of evaluating the integral. Evaluate the following definite integral:

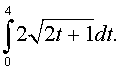
Solution: To integrate this integral we need to make the substitution u = 2t + 1, so du = 2dt. The endpoints are t = 0, which changes to u = 1, and t = 4, which becomes u = 9. Thus, the integral above is solved as follows:

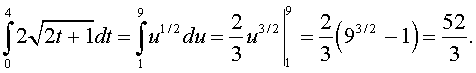
As usual, there are a collection of Worked Examples to help with the homework problems and give additional guidance on how to solve definite integrals.

Volume of the Dead Space

As noted in the notes above, the dead space for breathing is found by determining the area of the region to the left of the curve in the figure above. The area of that region can be approximated by the definite integral

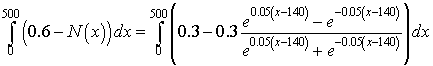
The integral above breaks down into two integrals to solve. The first is quite elementary, while the second requires substitutions. The first integral is simply

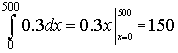
In the second integral, we make the substitution

Note that the limits of integration changes from x = 0 and x = 500 to

Thus, we can write the second integral as

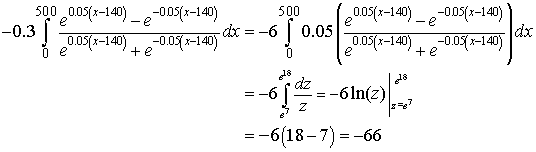
We combine the results above to give

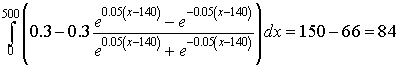
It follows that the measured volume of nitrogen N₂ lost in the deadspace to pure oxygen O₂ is 84 ml from the graph above. However, the limiting nitrogen in the graph above is only 60%, so the actual deadspace is 84/0.6 = 140 ml.