Math 121 - Calculus for Biology I Spring Semester, 2004 Rules of Differentiation - Examples
	© 2001, All Rights Reserved, SDSU & Joseph M. Mahaffy San Diego State University -- This page last updated 30-Dec-03

1. Differentiation with thePower Law
2. Rate of Change in Pulse
3. Velocity of a Ball

Below are examples of differentiation using the power rule developed in the main section. The applications extend the work of the pulse/weight example and throwing a ball into the air.

Examples of Differentiation - Power Rule

1. Find the derivative of the polynomial

Solution: From the power rule, we simply multiply the coefficient by the power of x, then reduce the power of x by 1. This gives

Notice that the derivative of any constant is zero.

2. Find the derivative of the function

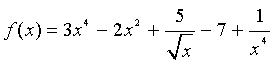
Solution: This problem is most easily worked by first changing all the terms in f(x) into terms that only include powers of x, then apply the power rule. Thus,

This is easily differentiated to give

 

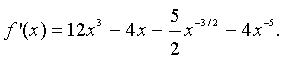
Example 2: Rate of Change in Pulse

In the lecture notes, we found that there was an allometric relationship between weight and the pulse of mammals given by the formula

Find the rate of change in the pulse with respect to the weight when an animal is 1 kg. Also, determine the rate of change in the pulse with respect to the weight when an animal is 81 kg. Which of the two calculated rates of change is larger in magnitude and what does this say about how pulse changes as weight increases?

Solution: From the lecture notes, we have that in general the derivative of P(w) is given by

It follows that P '(1) = -50 and P '(81) = -50(81)^-5/4 = -50(3)^-5 = -50/243 = -0.206. The pulse rate at w = 1 is larger in magnitude. Thus, the rate of change of the pulse rate at 1 kg is dropping much more quickly than the rate of change of the pulse rate at 81 kg. Thus, changes in pulse rate are much less between larger animals.

Example 3: Velocity of a Ball

A ball, thrown vertically from a platform without air resistance, satisfies the equation

Sketch a graph of the height of the ball, h(t), as a function of time, t. Find the maximum height of the ball and determine when the ball hits the ground. Give an expression for the velocity, v(t), as a function of time, t. Find the velocity at the times t = 0, t = 1, and t = 2. What is the velocity of the ball just before it hits the ground?

Solution: We begin by factoring, so h(t) = -16(t + 1)(t - 5). The height of the platform is clearly 80 ft, as h(0) = 80. From the factor, we see that the ball hits the ground at t = 5. The maximum height of the ball is at the vertex, which is halfway between the intercepts. Thus, the maximum occurs at t =2 with h(2) = 144 ft.

The velocity is given by the derivative of the height function, so

We see that v(0) = 64 ft/sec (the initial velocity), v(1) = 32 ft/sec, and v(2) = 0 ft/sec. As we expected, the velocity at the maximum is zero. The ball hits the ground with velocity v(5) = -96 ft/sec. Below is a graph of the height of the ball.