Math 121 - Calculus for Biology I
Spring Semester, 2004
Product Rule
San Diego State University -- This page last updated 03-Jan-04
|
|
Math 121 - Calculus for Biology I |
|
|---|---|---|
|
|
San Diego State University -- This page last updated 03-Jan-04 |
|
Many mathematical techniques are valuable for the study of cancer, including the mathematics of image processing, calculations of therapeutic doses, epidemiology of cancer in a population, and growth studies. This section begins with a model used to predict the growth of a tumor. This model introduces the product rule of differentiation to find when the tumor is growing most rapidly. The product rule is useful in other growth models and graphing.
Gompertz Model for Tumor Growth
Tumors can only grow as large as the nutrient supply available to the tumor cells. Tumor angiogenesis is the proliferation of blood vessels that penetrate into the tumor to supply nutrients and oxygen and to remove waste products. The center of the tumor largely consists of dead cells, called the necrotic center of the tumor. The tumor grows outward in roughly a spherical shell shape. If the tumor fails to produce signaling proteins for angiogenesis, then the tumor can only grow to a certain size with available nutrient supplies.
Simpson-Herren and Lloyd (1970) studied the growth of a number of tumors. One tumor they studied was the C3H Mouse Mammary tumor, which is stimulated by a provirus. By using tritiated thymidine, they measured the cell cycles for the mammary tumors in mice. From this, they were able to find the growth rate for these tumors. Below is a graph showing the population of tumor cells and the growth rate of the tumor at the various sizes of the tumor. (The graph includes the curve for the Gompertz model.)
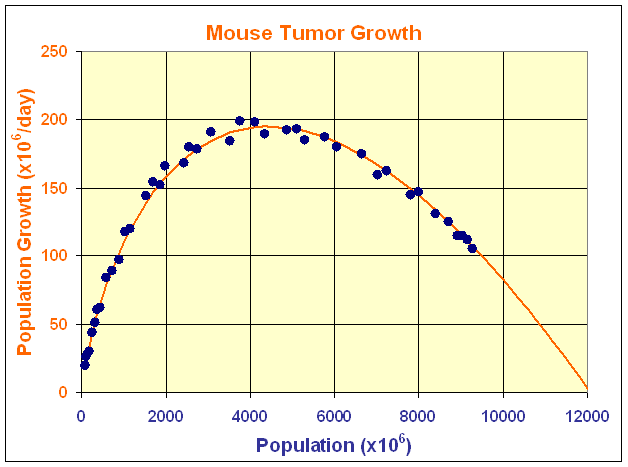
There have been a number of mathematical models that can closely match the growth of a tumor. Laird (1964) showed that tumor growth satisfies equations developed by Gompertz, provided the number of tumor cells is sufficiently large. The growth function is given by the equation
G(N) = N(b - a ln(N)),
where N are the number of tumor cells and a and b are constants that are matched to the data measuring the growth of a tumor. Note that this function is not defined for N = 0, so it is assumed that the tumor has a certain size before applying this model. For the data above, the best fit curve is given by
G(N) = N(0.4126 - 0.0439 ln(N)).
As with the logistic growth function, this function is zero when growth is zero or the growth of the tumor stops. When the growth of the tumor stops, the tumor cells are at equilibrium and the tumor is at its maximum size supportable with the available nutrient supply. We would also like to know when the tumor is growing most rapidly. This will occur when the derivative is zero.
The equilibrium is found when
G(N) = N(b - a ln(N)) = 0.
Since N > 0, this occurs when b - a ln(N) = 0. This is equivalent to
ln(N) = b/a
Ne = eb/a.
Thus, Ne = eb/a is the unique equilibrium and is similar to the carrying capacity seen for the logistic growth function. For the specific data given above, the
Ne = e0.4126/0.0439 = = e9.399 = 12,072,
which matches the P-intercept on the graph above.
Finding the derivative of G(N) presents a new problem in differentiation. We need to develop the product rule for differentiation to differentiate G(N).
Let f(x) and g(x) be differentiable functions. The product rule for finding the derivative of the product of these two functions is given by:
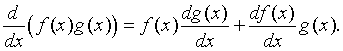
In words, this says that the derivative of the product of two functions is the first function times the derivative of the second function plus the second function times the derivative of the first function.
Example 1: We begin by verifying the product rule with a simple example. Consider f(x) = x5. We know that f '(x) = 5x4. Let f1(x) = x2 and f2(x) = x3, then f(x) = f1(x) f2(x). From the product rule we have
f '(x) = f1(x) f2'(x) + f1'(x) f2(x) = x2(3x2) + (2x)x3 = 5x4.
Maximum Growth for the Gompertz Tumor Growth Model
To find the maximum growth, we apply the Product Rule to the Gompertz Growth function
G(N) = N(b - a ln(N)),
giving
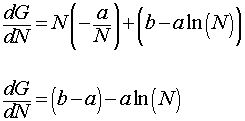
The maximum occurs when G '(N) = 0, which is when
a ln(Nmax) = b - a.
Nmax = e(b/a - 1).
If we apply this to the Gompertz model for the mouse mammary tumor, then we find that the maximum occurs at the population
Nmax = e(9.399 - 1) = 4,441 (x106).
This value is substituted into the Gompertz growth function and gives the maximum growth of mouse mammary tumor cells as
G(Nmax) = 4441(0.4126 - 0.0439 ln(4441)) = 195.0 (x106/day).
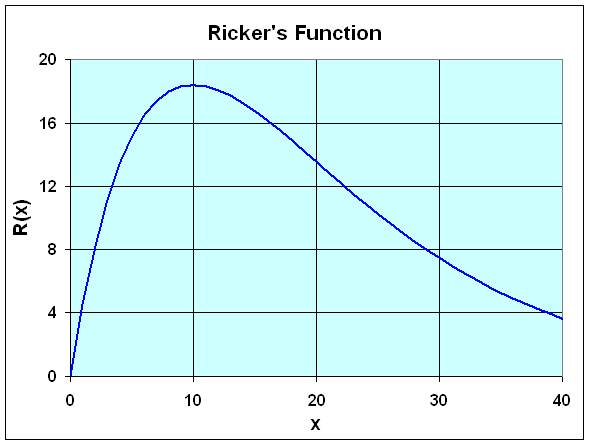
Example 2: Consider the Ricker's function R(x) = 5x e-0.1x. (We will see this function in later population studies.) Let us sketch a graph of this function, finding all extrema and points of inflection.
Solution: First we note that the only intercept is the origin, (0, 0). Next we use the product rule to differentiate this function.
Since the exponential function is never zero, R '(x) = 0 implies that the only critical point satisfies 1 - 0.1x = 0 or x = 10. Thus, there is a maximum at (10, 50 e-1) or (10, 18.4).
Next we take the second derivative or the derivative of R '(x). Again we use the product rule to obtain
The point of inflection is found by solving R ''(x) = 0, which is very similar to our equation for the critical point. Its not hard to see that the point of inflection occurs at x = 20. Thus, there is a point of inflection at (20, 100 e-2) or (20, 13.5).
[1] A. K. Laird (1964), Dynamics of tumor growth, Brit. J. Cancer 18, 490-502.
[2] L. Simpson-Herren and H. H. Lloyd (1970), Kinetic parameters and growth curves for experimental tumor systems, Cancer Chemother. Rep. Part I, 54, 143-174.