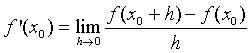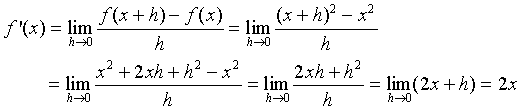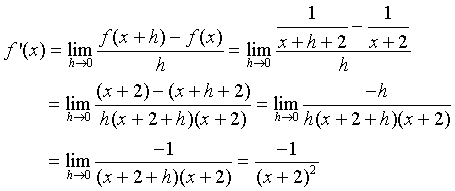1. Limits
2. Continuity
3. Derivative

• This is a theoretical section that studies the concepts of limits, continuity, and the derivative
• The definition of the derivative is presented
• This section sketches the formal mathematics needed for the derivative
• A complete understanding is beyond the scope of this course
• Earlier noted how the derivative is related to the slope of tangent line for a curve at a point

Limits

• Conceptually, the limit of a function f(x) at some point x₀ simply means that if your value of x is very close to the value x₀, then the function f(x) stays very close to some particular value.

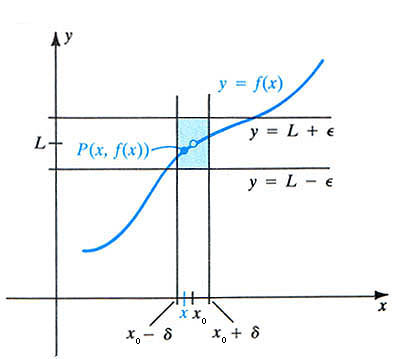
Definition: The limit of a function f(x) at some point x₀ exists and is equal to L if and only if every "small" interval about the limit L, say the interval (L - e, L + e), means you can find a "small" interval about x₀, say the interval (x₀ - d, x₀ + d), which has all values of f(x) existing in the former "small" interval about the limit L, except possibly at x₀ itself.

• This is a difficult concept to fully appreciate. However, you should be able to grasp the idea through several examples.

Examples:

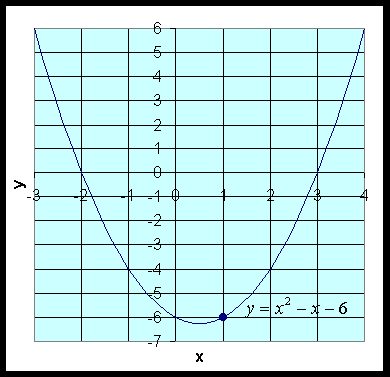
1. f(x) = x² - x - 6

• Find the limit as x approaches 1
• From either the graph or from the way you have always evaluated this quadratic function that as x approaches 1, f(x) approaches -6, since f(1) = -6.

Fact: Any polynomial, p(x), has as its limit at some x₀, the value of p(x₀).

2. The rational function

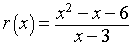
• Find the limit as x approaches 1
• If x is not 3, then this rational function reduces to r(x) = x + 2
• So as x approaches 1, this function simply goes to 3.

Fact: Any rational function, r(x) = p(x)/q(x), where p(x) and q(x) are polynomials with q(x₀) not zero, then the limit exists with the limit being r(x₀).

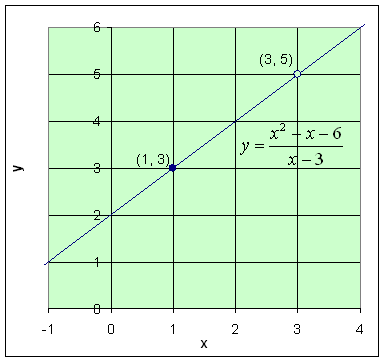
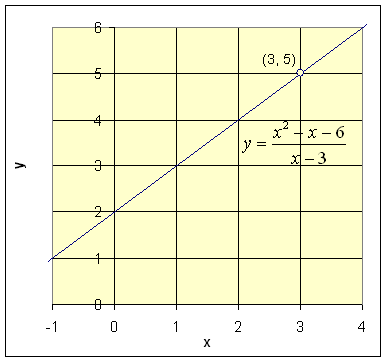
3. The rational function in Example 2.

• Find the limit as x approaches 3
• Though r(x) is not defined at x₀ = 3, arbitrarily "close" to 3, r(x) = x + 2
• So as x approaches 3, this function goes to 5
• Its limit exists though the function is not defined at x₀ = 3.

4. Consider the rational function f(x) = 1/x²

• Find the limit as x approaches 0, if it exists
• This function has a limit for any value of x₀ where the denominator is not zero
• However, at x₀ = 0, this function is undefined
• Thus, the graph has a vertical asymptote at x₀ = 0
• This means that no limit exists for f(x) at x₀ = 0

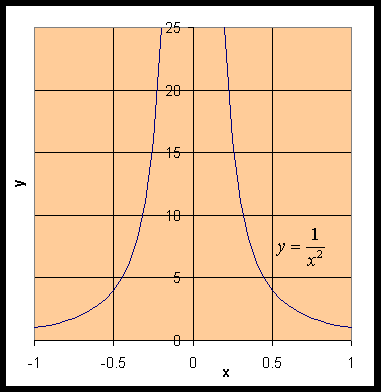
Fact: Whenever you have a vertical asymptote at some x₀, then the limit fails to exist at that point.

5. The rational function

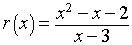
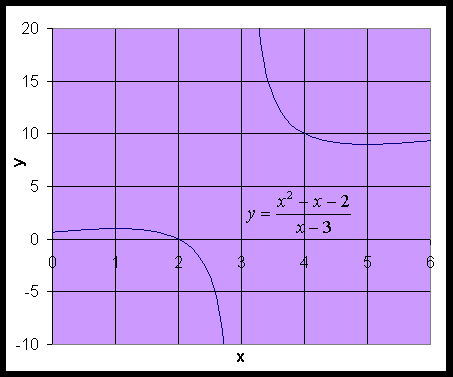
• Find the limit as x approaches 3, if it exists
• This function has a limit for any value of x₀ where the denominator is not zero
• However, at x₀ = 3, this function is undefined
• The function is not approaching zero in the numerator near x₀ = 3
• Thus, the graph would show a vertical asymptote at x₀ = 3
• This means that no limit exists for r(x) at x₀ = 3

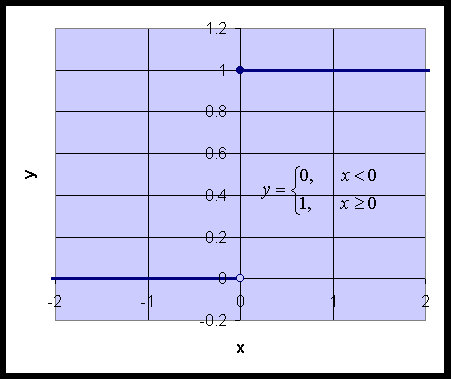
6. The Heaviside function is often used to specify when something is "on" or "off." The Heaviside function is defined as

 

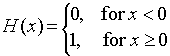
• This function clearly has the limit of 0 for any x < 0, and it has the limit of 1 for any x > 0
• Even though this function is defined to be 1 at x = 0, it does not have a limit at x₀ = 0
• If you take some "small" interval about the proposed limit of 1, say e = 0.1, then all values of x near 0 must have H(x) between 0.9 and 1.1
• But take any "small" negative x and H(x) = 0, which is not in the desired given interval
• Thus, no limit exists for H(x)

Perspective: Whenever a function is defined differently on different intervals in a manner similar to the Heaviside function above, you need to check the places where the function changes in definition to see if the function has a limit at these x values where the function changes. (It might also have asymptotes at other points where again you would check.)

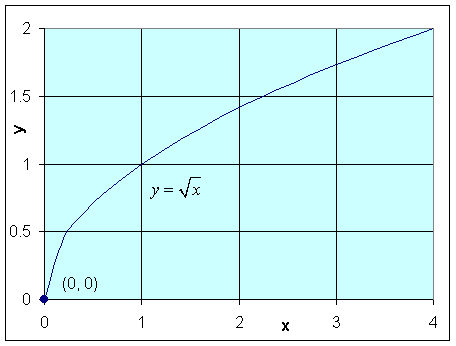
7. The fractional power function f(x) = x^1/2

• Find the limit as x approaches 0, if it exists
• This function is not defined for x < 0, so it cannot have a limit at x = 0, though it is said to have a right-handed limit

Summary of Limits: Most of the functions that you regularly examine have limits. Usually, the problems arise at points x₀ when there is a vertical asymptote, the function is defined differently on different intervals, or special cases like the square root function.

Continuity

• Closely connected to the concept of a limit is that of continuity
• Intuititvely, the idea of a continuous function is what you would expect
• If you can draw the function without lifting your pencil, then the function is continuous
• Most practical examples use functions that are continuous or at most have a few points of discontinuity

Definition: A function f(x) is continuous at a point x₀ if the limit exists at x₀ and is equal to f(x₀).

• The examples above should also help you appreciate this concept
  • In all of the cases except Example 3, the existence of a limit also corresponds to points of continuity
  • Example 3 is not continuous at x₀ = 3 though a limit exists here, as the function is not defined at 3
  • Examples 3 and 5 are discontinuous only at x₀ = 3
  • Examples 4, 6 and 7 are discontinuous only at x₀ = 0
  • At all other points in the domains of these examples are continuous.

Example Comparing Limits and Continuity

• An example is provided to show the differences between limits and continuity
• Below is a graph of a function, f(x), that is defined on the interval [-2, 2], except at x = 0, where there is a vertical asymptote

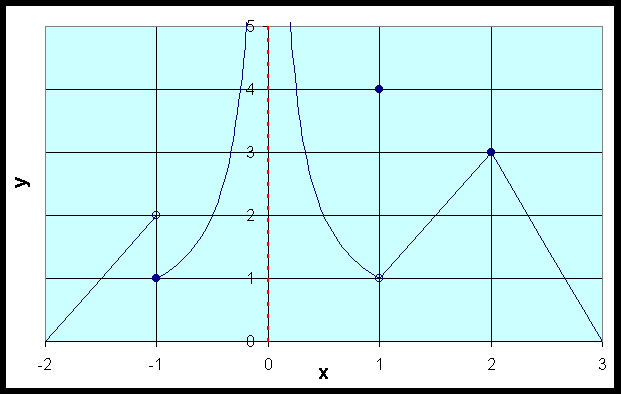
• The difficulties with this function occur at integer values
• At x = -1, the function has the value f(-1) = 1
  • It is clear that the function is not continuous nor does a limit exist at this point
• At x = 0, the function is not defined (not continuous nor has any limits) as there is a vertical asymptote
• At x = 1, the function has the value f(1) = 4
  • The function is not continuous at x = 1, but the limit does exist with

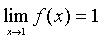
• At x = 2, the function is continuous with f(2) = 3, which also means that the limit exists
• At all non-integer values of x the function is continuous (hence its limit exists)

Derivative

• The primary reason for the discussion above is for the proper definition of the derivative
• In the previous sections, we noted that the derivative at a point on a curve is the slope of the tangent line at that point
• This motivation is what underlies the definition given below

Definition: The derivative of a function f(x) at a point x₀ is denoted by f '(x₀) and satisfies

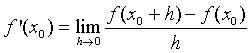
provided this limit exists.

Examples:

1. Let us use this definition to find the derivative of f(x) = x².

 

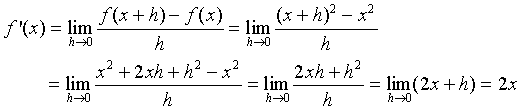
2. We repeat this computation to find the derivative of f(x) = 1/(x + 2) (for x not equal to -2).

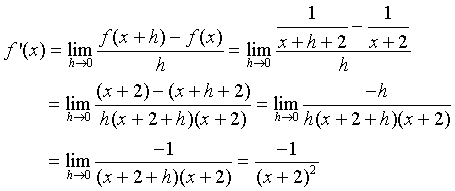
• Clearly, we do not want to use this formula every time we need to compute a derivative
• The next section gives much easier formulae for finding derivatives
• Another very easy way to find derivatives is using the Maple diff command
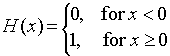