1. Rate of mRNA synthesis
2. Definition and Properties of Functions
   1. Definition of Function
   2. Addition and Multiplication of Functions
   3. Composition of Functions
3. Worked Examples
4. Quadratic Equations and Quadratic Functions
   1. Weak Acid Example
   2. Quadratic Equations
   3. Quadratic Functions
5. References

• Biological problems are rarely linear
• Begin with study of Escherichia coli
  • Linear model for mRNA synthesis
  • Quadratic function to find the least squares best estimate
• General study of functions - Mathematical definitions
• Review quadratic functions

Rate of mRNA synthesis

• DNA replication cycle in E. coli provides the genetic code for all of the proteins
• Used either directly or indirectly for all aspects of the growth, maintenance, and reproduction of the cell
• The synthesis of proteins follows the processes of transcription and translation

Transcription of a bacterial gene is a controlled sequence of steps, where the protein, RNA polymerase, reads the genetic code and produces a complementary messenger RNA (mRNA) template. This mRNA is a short-lived blueprint for the production of a specific protein that has some particular activity in the bacterial cell.

Translation of the mRNA in bacteria begins shortly after transcription starts, with ribosomes (consisting of ribosomal RNA and ribosomal proteins) reading the triplet codons on the mRNA. The ribosome sequentially assembles a series of amino acids (based on the specific codons read), which form a polypeptide. It is believed that the physical properties of the atoms in the polypeptide cause it to fold passively into a tertiary structure that either becomes an active protein or, when combined with other elements from the cell (such as another polypeptide or lipids), becomes an active protein or enzyme.

• The rate of growth of a bacterial cell depends on the rate at which it assembles all of its cellular components inside the cell
• The rate of production of different components inside the cell varies depending on the length of time it takes for a cell to double
• The table below shows the doublings/hr, denoted m, and the rate of mRNA synthesis/cell, denoted r_m.

• Instability of the mRNA implies its rate of production closely approximates the rate of growth of a cell
• The data lie almost on a straight line passing through the origin
• Linear mathematical model of the form

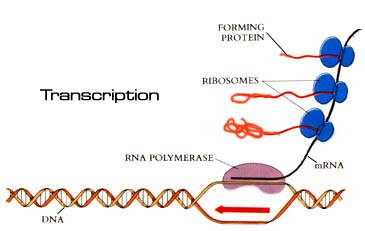
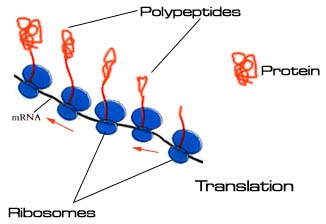
for some value of a, which is the slope of the linear model.

• The linear least squares best fit of this model to the data uses only the slope of the model, a
• The sum of the squares of the errors is computed from each of the error terms:
  1. e₁² = (4.3 - 0.6a)²
  2. e₂² = (9.1 - a)²
  3. e₃² = (13 - 1.5a)²
  4. e₄² = (19 - 2a)²
  5. e₅² = (23 - 2.5a)²

• Squared these terms and add them together to give

  J(a) = 13.86a² - 253.36a + 1160.3

• J(a) is a quadratic function representing the sum of the squares of the errors
• The best fit of the model is the smallest value of J(a)
• This is the vertex of this quadratic equation

• Below, an applet allows the manipulation of the slope, a, of the line to fit the data
• On the right is the value of the quadratic function, J(a)
• The best fit to the data occurs at the vertex of the parabola traced by J(a)
• The vertex of the parabola is (a, J(a)) = (9.14, 2.45)

Alternate link

Definitions and Properties of Functions

• Functions form the basis for most of this course
• A function is a relationship between one set of objects and another set of objects with only one possible association in the second set for each member of the first set
• mRNA example has two functions
  1. A set of possible cell doubling times, m, to which was found a particular average rate of mRNA synthesis, r_m. (This subdivides into two functional representations: 1. The experimental data, which represents a function with a finite set of points, or 2. The linear model, which creates a different function representing your theoretical expectations.)
  2. The sum of the squares of the errors between the data points and the model, J(a), forms another function, where the set of possible slopes, a, in the model, each produced a number, J(a), representing how far away the model was from the true data. (Claim that the best model is when this function is at its lowest point.)
• Calculus helps determine the lowest or minimum value of a function.

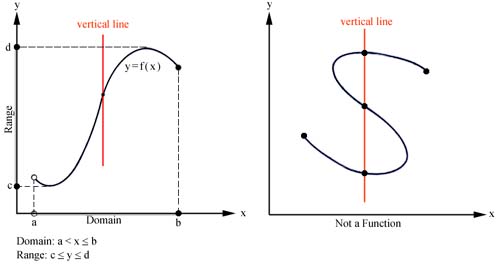
Function: A function of a variable x is a rule f that assigns to each value of x a unique number f(x). The variable x is the independent variable, and the set of values over which x may vary is called the domain of the function. The set of values f(x) over the domain gives the range of the function.

Often a function is described by a graph in the xy-coordinate system. By convention x is the domain of the function and y is the range of the function. The graph is defined by the set of points (x, f(x)) for all x in the domain.

The vertical line test states that a curve in the xy-plane is the graph of a function if and only if each vertical line touches the curve at no more than one point.

Addition and multiplication of functions are carried out symbolically by standard algebraic techniques.

Example 1: Let f(x) = x - 1 and g(x) = x² + 2x - 3. Determine f(x) + g(x) and f(x)g(x).

Solution: The addition of the two functions satisfies:

f(x) + g(x) = x - 1 + x² + 2x - 3 = x² + 3x - 4.

The product or multiplication of the two functions is given by:

f(x)g(x) = (x - 1)(x² + 2x - 3) = x³ + 2x² -3x - x² - 2x + 3 = x³ + x² - 5x + 3.

Example 2: Determine f(x) + g(x) for

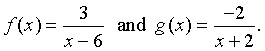
Solution: In this case, the addition of the two functions is simplified by finding a common denominator

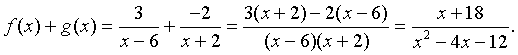
Composition of Functions is another important operation. Given functions f(x) and g(x), the composite f(g(x)) is formed by inserting g(x) wherever x appears in f(x).

Example 3: Let f(x) = 3x + 2 and g(x) = x² - 2x + 3. Determine f(g(x)) and g(f(x)).

Solution: The two composite functions are readily evaluated by substituting one of the functions in for x in the other function. We see that

f(g(x)) = 3( x² - 2x + 3) + 2 = 3x² - 6x + 11,

while

g(f(x)) = (3x + 2)² - 2(3x + 2) + 3 = 9x² + 6x + 3.

More Worked Examples are provided on a hyperlinked page.

Quadratic Equations and Quadratic Functions

• Review of quadratic equations and the graphing of quadratic functions (parabolas) from the prerequisite algebra course
• The weak acids provide a classic problem in Chemistry that uses of the quadratic equation.

Weak Acids

• Many of the organic acids found in biological applications are weak acids.
• Weak acid chemistry is important in preparing buffer solutions for laboratory cultures.

• Formic acid (HCOOH) is a relatively strong weak acid that ants use as a defense.
• The strength of this acid makes the ants very unpalatable to predators.
• The chemistry of dissociation is given by the following equation:

• Each acid has a distinct equilibrium constant K_a that depends on the properties of the acid and the temperature of the solution.
• For formic acid, K_a = 1.77×10^-4.
• Let [X] denote the concentration of a particular chemical species X.
• Formic acid is in equilibrium, when it satisfies the following equation:

• If formic acid is added to water, then [H⁺] = [HCOO^-].
• If x is the normality of the solution, then x = [HCOOH] + [HCOO^-].
• It follows that [HCOOH] = x - [H⁺], so

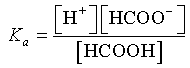
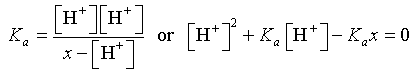
which is a quadratic equation in [H⁺] and is easily solved using the quadratic formula.

The solution is given by

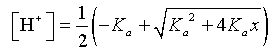
Only the positive solution is taken to make physical sense.

Example 4: Find the concentration of [H⁺] for a 0.1N solution of formic acid.

Solution: Since formic acid has K_a = 1.77×10^-4 and we have a 0.1N solution of formic acid, then we can substitute into the formual given above to yield:

Thus, the concentration of acid in the 0.1 N solution is [H⁺] = 4.12 ×10^-3, which gives a pH of 2.385. (Note that pH is defined to be -log₁₀ [H⁺].)

Review of Quadratic Equations

Quadratic equations: The general quadratic equation is given by the formula:

Two methods for solving quadratics:

1. Factoring the equation
2. The quadratic formula, which has the form

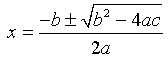
In the example above, the quadratic formula was needed because we didn't know either K_a or x.

Example 5 (Factoring): Consider the following quadratic equation:

Find the values of x that satisfy this equation.

Solution: The equation above is easily factored to give the solution.

Example 6 (Quadratic formula): Find the roots of the quadratic equation:

Solution: The quadratic formula gives

Quadratic Functions

• The general form of a quadratic function is

where a is a nonzero constant and b and c are arbitrary.

• The graph of this function

produces a parabola.

• For each value of x, there is only one value of y. However, for most values of y in the range of this function, there are two values of x. (A horizontal line intersects the graph in two places.)

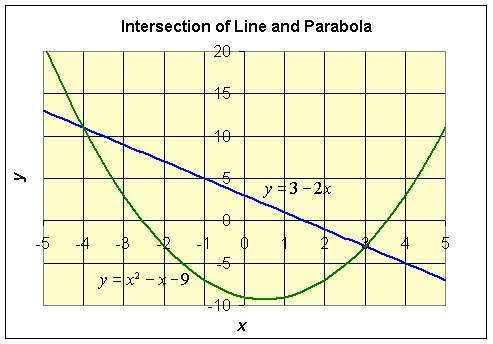
Example 5: Find the intersections of the line y = 3 - 2x and the quadratic function

Sketch a graph of these functions.

Solution:

• Find the points of intersection by setting the equations equal to each other.

• This equation is easily factored giving

so x = -4 or 3.

• The y values corresponding to x = -4 and 3 give the points of intersection as (-4, 11) and (3, -3).

More Worked Examples are provided on a hyperlinked page.

References:

[1] H. Bremer and P. P. Dennis, "Modulation of chemical composition and other parameters of the cell by growth rate," Escherichia coli and Salmonella typhimurium, ed. F. C. Neidhardt, American Society of Microbiology, Washington, D.C., 1987.