![]()
Math 121 - Calculus for Biology I
Spring Semester, 2008
San Diego State University -- This page last updated 28-Feb-08
|
|
Math 121 - Calculus for Biology I |
|
|---|---|---|
|
San Diego State University -- This page last updated 28-Feb-08 |
Below are a collection of problems that use the techniques developed in the Discrete Malthusian Growth section.
Example 1:
a. One species of insect grows according to the discrete Malthusian growth model
where n represents the number of weeks after some initial time and Hn is the population at the end of the nth week. Find the population at the end of the first three weeks, H1, H2, and H3. Also determine how long it takes for this population to double.
b. Another insect species starts with a smaller population, but grows more quickly. It satisfies the discrete Malthusian growth model
Find the doubling time of this population of insects and determine how long until the populations of the two species are equal.
Solution:
a. According to the model,
H1 = 1.06H0 = 1.06(50,000) = 53,000.
Thus, H2 = 1.06H1 = (1.06)2(50,000) = 56,180 and H3 = 1.06H2 = (1.06)3(50,000) = 59,551.
This model can be rewritten as
Hn = (1 + 0.06)nH0.
When the population doubles, 2H0 = (1 + 0.06)nH0. First divide each side by H0, then take the natural log of both sides and solve for n. The result is as follows:
n = ln(2)/ln(1.06) = 11.90
The result can be rounded up to the nearest integer to obtain n = 12. Thus, the population doubles after 12 weeks.
b. The population doubling time for the second species Gn can be found using the same method used in Part a of this example. Thus, we obtain
Notice that the doubling time is shorter for this species than for the species in Part a, as expected. This is due to the higher growth rate (1.08 > 1.06).
When the two populations are equal, we can say Gn+1 = Hn+1. Thus, we obtain
10,000(1.08)n = 50,000(1.06)n
(1.08)n = 5(1.06)n
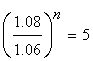
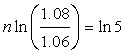
n = 86.10
So the two populations are approximately equal after 86 weeks.
A subject closely related to Malthusian growth is the process of compound interest. Start with an initial principal P0 and an annual interest rate of r, then the principal n years later is found by the same equation as given above for Malthusian growth. That is
Now suppose that the interest is compounded more frequently than annually. For example, if the interest was compounded quarterly, then each quarter would have an interest rate of r/4. Also, if n is the number of years that we want to compute, then the formula for finding Pn is given by
since each quarter has 1/4 the annual interest rate, but now we are computing the amount of interest 4 times (4n) as often, or four times each year.
The general formula for determining the amount of principal when the interest rate is r (annual), which is compounded k times a year for n years, given an initial amount of P0 satisfies:
Pn = (1 + r/k)knP0.
Example 2: Suppose you begin with $2,000 to invest. Bank A offers 6.25% interest compounded annually, while Bank B offers 6% interest compounded monthly. Which of these investments gives the better return?
Solution:
Using the model above for Bank A, we have k = 1, r = 0.0625, and P0 = $2,000. For Bank B, k = 12, r = 0.06, and P0 is also $2,000. After one year, the balances at Bank A and Bank B are, respectively
P1B = (1 + 0.06/12)12($2,000) = $2,123.36
So Bank A has a slightly better return.
Compound Interest Related to Population Studies
In population studies, one can use this concept to examine growth rates for a population growing according to the Malthusian growth model for differing periods of time. For example, our model above on the U. S. census had a growth rate of approximately 35% per decade in the early years. The question arises as to what the appropriate annual rate of growth would be.
Notice if we simply divide the 35% growth rate by 10 years the population predictions will be significantly different. Each 1 million people in a population using the growth rate of 35% results in 1,350,000 people at the end of a decade. However, the compounded interest formula with 3.5% per year would give
which is about 6% higher than the amount using the 35% per decade growth rate.
So what is the appropriate annual growth rate, and how do we find it? The given information is 35% growth in a decade. If we let r be the annual growth rate, then we need to solve the equation
This is easily solved by taking the 10th root of each side. So
Thus, the appropriate annual growth rate for the population of the U. S. near 1800 was about 3% per year.
Example 3: The population in the U. S. was 203.3 million in 1970 and 226.5 million in 1980. Assume that the population is growing according to the discrete Malthusian growth model and find the annual growth rate of the population during this period of time. Use this information to project the population in 1990. The actual census gives the population in 1990 to be 248.7 million, so what is the percent error between the actual population and the modeling prediction?
Solution:
The population growth rate per decade is calculated to obtain
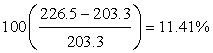
Thus, we need to solve the equation
Taking the 10th root of each side, we obtain
The discrete Malthusian model can then be used as follows, where P is in millions
For n = 20 years in 1990, we obtain a population of
With respect to the actual census value of 248.7 million, the percent error of this model is
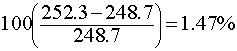
in the year 1990
Example 4: A population of arthropods is growing in a lake that begins to receive pesticide runoff from neighboring farm fields. The resulting pollution adversely affects the rate of growth of their population. Suppose that these arthropods multiply according to the dynamics of the nonautonomous Malthusian growth model given by
where n represents the number of weeks after some initial time, k(tn) = 0.1 - 0.02 n, and An is the population density at the end of the nth week. Find the population at the end of the first three weeks, A1, A2, and A3. Find the maximum population density of these arthropods and when this occurs. Also, determine when the lake becomes so polluted that the arthropod population dies out.
Solution: Unlike the discrete Malthusian growth model, the exact solution to this problem uses very complex mathematics. Still the model is very simple to simulate, and it is easy to analyze certain aspects of the problem such as when the growth levels off and when extinction occurs. Below is a table showing the population density of the arthropods for the first 10 weeks.
|
|
Arthropods |
|
0 |
200 |
|
1 |
220 |
|
2 |
238 |
|
3 |
252 |
|
4 |
262 |
|
5 |
267 |
|
6 |
267 |
|
7 |
262 |
|
8 |
251 |
|
9 |
236 |
|
10 |
217 |
The maximum population density occurs when the growth rate goes to zero, so k(tn) = 0, which happens when n = 5. The population goes to extinction when 1+ k(tn) = 0. This occurs at the end of 55 weeks.