|
|
Math 121 - Calculus for Biology I |
|
|---|---|---|
|
|
San Diego State University -- This page last updated 26-Oct-02 |
|
|
|
Math 121 - Calculus for Biology I |
|
|---|---|---|
|
|
San Diego State University -- This page last updated 26-Oct-02 |
|
Examples of Exponential and Logarithmic Functions
Example 1: Solve the equation
ex-2 = 3.
Solution:
Taking the natural logarithm of both sides gives
so
Example 2: Solve the equation
ln(2x + 1) = 4.
Solution:
Exponentiating both sides, we find
so
x = ( e4 - 1)/2.
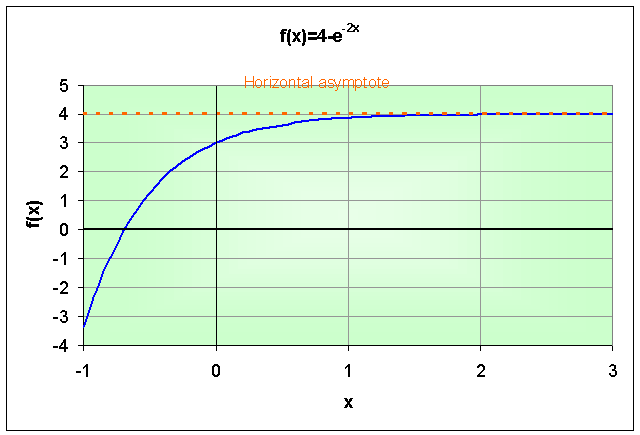
Example 3:Graph the equation
f(x) = 4 - e-2x.
Determine all intercepts and any horizontal asymptotes.
Solution:
When x = 0,
f(0) = 4 - e0 = 4 - 1 = 3.
Thus, the y-intercept is (0,3).
Solving 4 - e-2x = 0, gives
e-2x = 4 or e2x = 1/4.
Thus, 2x = ln(1/4) = ln(2-2) = -2ln(2) or x = -ln(2) = -0.6931.
Therefore, the x-intercept is (-0.693,0).
For large values of x, e-2x is very close to zero, so there is a horizontal asymptote for large positive x with f(x) tending toward 4.
The graph is shown below.
Example 4: Graph the equation
f(x) = ln(x + 2).
Determine all intercepts and any vertical asymptotes.
Solution:
The domain of f(x) is x > -2.
When x = 0,
f(0) = ln(2) = 0.6931.
Thus, the y-intercept is (0,0.693).
Solving ln(x + 2) = 0, gives
x + 2 = 1 or x = -1.
Thus, the x-intercept is (-1, 0).
There is a vertical asymptote at the edge of the domain, where x = -2.
The graph is shown below.

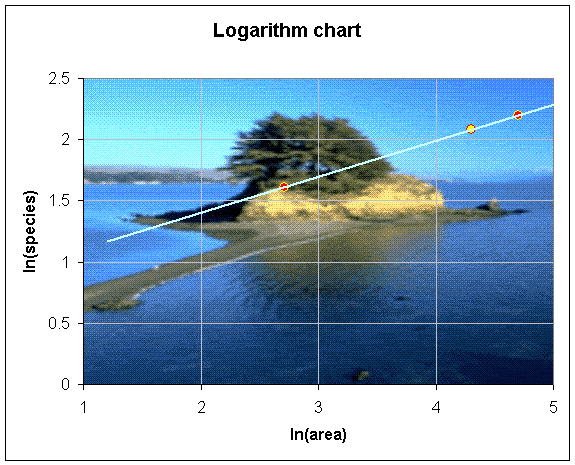
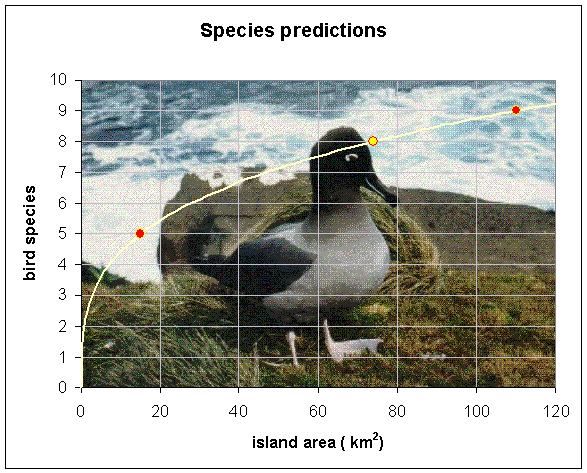
Example 5: There are three Pacific islands in a chain. Island A is 15 km2, Island B is 110 km2, and Island C is 74 km2. An extensive biological survey finds 5 species of birds on Island A and 9 species of birds on Island B.
a. Assume a power law relationship between the number of species (N ) on each of these islands and their area (A) of the form
N = kAx.
Use the data from Islands A and B to determine the constants k and x. Use this expression to predict the number of species on Island C.
b. How large of an island would be required to support 20 species of birds near this chain of islands?
Solution:
a. Taking the natural logarithm of both sides of the given power law relationship and then solving for slope x, we obtain
ln(N) = ln(k) + x ln(A)
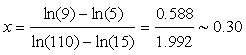
We can use this slope with either of the points (A, N) to find ln(k)
ln(5) = ln(k) + 0.30 ln(15)
ln(k) = ln(5) - 0.30 ln(15) = .797
k ~2.2
So the power law relationship is given by
N = 2.2 A0.30
We can now predict the number of species on Island C
N = 2.2(74)0.30 = 8
Thus, there should be 8 species on Island C.
A graph with the data, model, and prediction.
b. We can use this model to predict the size of an island necessary to support 20 species as follows:
20 = 2.2A0.30
Solving for A,
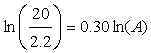
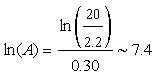
Exponentiating both sides, we find the island area A = 1636 km2.
A graph of the logarithms of the data and the straight line fit that the allometric model gives.