1. Cumulative AIDS cases
2. Allometric or Power Law Model
3. Finding Allometric Models
4. Log-Log Graphs
5. References
6. Problems

Cumulative AIDS cases

The advent of AIDS in modern society has had a significant impact on both personal behavior and public policy. The new protease inhibitors have significantly improved the quality of life for those who are HIV positive; however, this has come at a substantial cost to society. The new drugs are extremely expensive, are difficult to take because of the complex scheduling requirements to be effective, and have many strong side effects (besides not always working for a particular person or strain of the HIV virus). In turn, there are a number of people who are now avoiding safe sex practices as they no longer fear the "Death Sentence" that used to be associated with an HIV infection.

There is an important need for our society to know the extent of this disease from both an economic and sociological perspective. In order to make informed public policy, we need to know what is the expected case load in the upcoming years. However, it is clearly an extremely complex modeling problem. Below is a table of cumulative cases of AIDS between 1981 and 1992 [1].

A quick glance at the data will clearly show that it is not linear, so a linear model is not appropriate.

Allometric or Power Law Model

The technique that we'll develop in this section is known as the Power Law of Modeling. It is also referred to as Allometric Modeling. This method is used regularly in modeling complex biological phenomena where the actual mechanisms underlying the model behavior are too complex to describe in detail, but there is a need to be able to make some predictions. This modeling technique assumes a relationship between two sets of data, x and y, that satisfy a power law of the form

where A and r are parameters that are chosen to best fit the data. Note that this model assumes that when x = 0, then y = 0. As always, you should be aware of the limitations of this type of modeling. This method provides its best predictive capabilities when examining a situation that lies between the given data points. For example, if the number of species of herptofauna on Carribean islands is determined for a collection of islands with varying areas, then this model would give a reasonable estimate for the expected number of species on another Carribean island with an area that lies between the collected data. It would not be appropriate for extending to a large continent as the area is significantly beyond the range of the collected data. It wouldn't even be appropriate for another island such as Iceland, which lies in a different type of climate and has a different geography.

For the data above, an allometric model that would be appropriate is to let x be time in years since 1980 and y be the cumulative AIDS cases. As we will show later, the best fit power law for this model is given by

and is shown in the graph below.

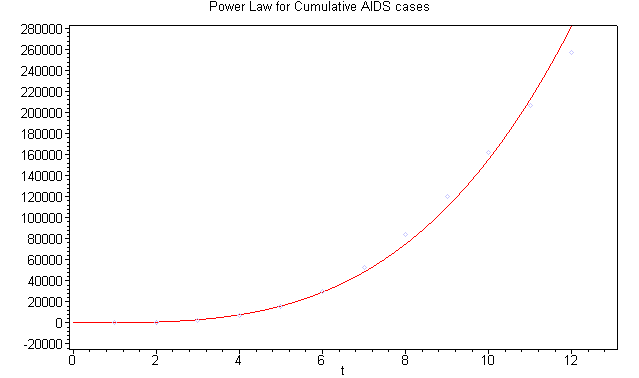
The graph shows that the power law provides a reasonable fit to the data. Unfortunately, the fit is weakest at the end where we'd like to use the model to predict the cumulative AIDS cases for the next year. The model predicts 366,990 cases in 1993, which is clearly too high from the given data. However, the analysis does give some indication of the rate of growth for this disease, which provides a first approximation for improved models and could be applied to expected spread of another disease with similar infectivity as HIV. This modeling technique is still valuable for analysis of many other data sets and occasionally can provide insight into the underlying biology of the problem. We will see more examples of this in the computer labs.

Below we will show the method for determining the parameters A and r in the model. First, we need to review the properties of exponents and logarithms.

Finding Allometric Models

We return to the Allometric model developed above, where two sets of data, x and y are assumed to satisfy a power law of the form

We want to choose the parameters A and r that best fit the data. The next step is to take the logarithm of both sides, then use the properties of logarithms to simplify the equation.

From this formula, we see that if we take the logarithm of the data, ln(x) and ln(y) and graph it we should see a straight line. That is, if we take X = ln(x), Y = ln(y), and a = ln(A), then the above equation can be written Y = a + rX , which is a line with a slope of r and a Y-intercept of ln(A).

We return to the example at the beginning of this section. Below is a table that includes both the data and the logarithms of the data.

Below shows a graph of the logs of the data (year-1980 and cumulative AIDS cases) along with the best straight line fit.

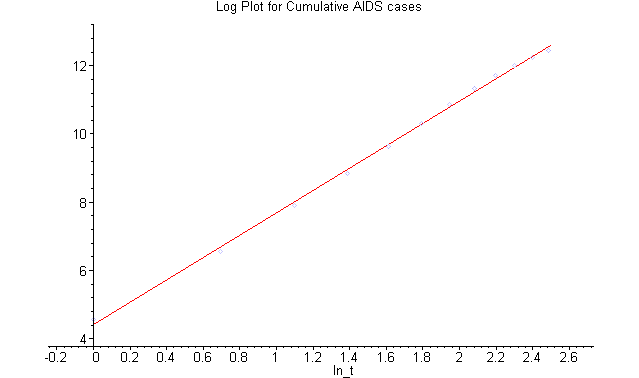
The plot above shows that when the logarithms of the data for the cumulative AIDS cases are plotted against the logarithms of the time since 1980, then these logarithmic data lie fairly close to a straight line. The least squares best fit of the straight line to the logarithms of the data give a slope of r = 3.274 and intercept of a = ln(A) = 4.415, which gives A = 82.70. Whenever this is the case, then an allometric or power law model makes a reasonable description of the data.

Log-Log Graphs

There exist graphing routines that readily create what is known as a log-log plot. This allows the user to simply graph the data directly onto a graph with logarithmic scales on the axes to see if the data falls on a straight line suggesting an allometric or power law model. Below we show a plot of the original data on cumulative AIDS cases against the date - 1980 on a graph with logarithmic scaled axes.

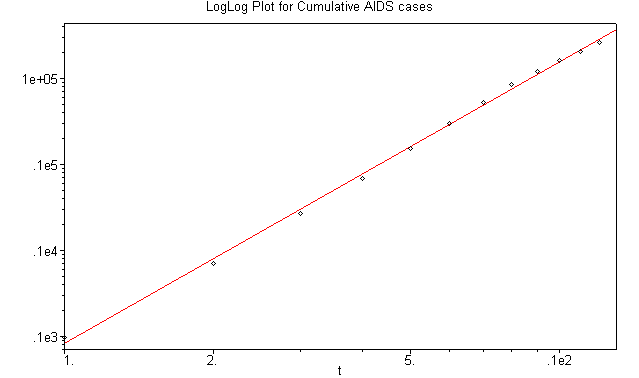
Example: Consider the relationship between weight and pulse. We know that smaller animals have a higher pulse than larger animals. Let us assume that this relationship satisfies an allometric model. Later in Lab we will perform a more detailed study of this phenomenon to check on the validity of using the allometric model (or power law).

We are given that a 17 g (or .017 kg) mouse has a pulse of 500 beats/min. Assume a 68 kg human has a pulse of 65. Let us use these data to form an allometric model and predict the pulse for a 1.34 kg rabbit. The power law gives

Next we take logarithms to obtain:

As noted above, this is a straight line in ln(P) and ln(w) with slope of k and intercept of ln(A). From the data,

Animal	Weight (kg)	ln(w)	Pulse (beats/min)	ln(P)
Mouse	0.017	-4.075	500	6.215
Human	68	4.220	65	4.174

The slope k is given by:

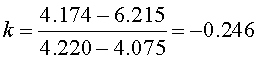
We can use this slope with one of the points to find ln(A) as follows:

Thus,

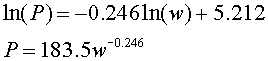
If we use the first equation with a 1.34 kg rabbit, then it gives P = 171.

Kepler's Third Law

This example relates to Kepler's Third Law. We will use the power law to determine the period of revolution about or distance from the sun for all planets given information about some of the planets. Let d be the mean distance (x10 ⁶ km) from the sun and p be the period of revolution in days about the sun. Here are data on four of the planets:

Planet	Distance d	ln(d)	Period p	ln(p)
Mercury	57.9	4.059	87.96	4.477
Earth	149.6	5.008	365.25	5.901
Mars	227.9	5.429	687.0	6.532
Jupiter	778.3	6.657	4337	8.375

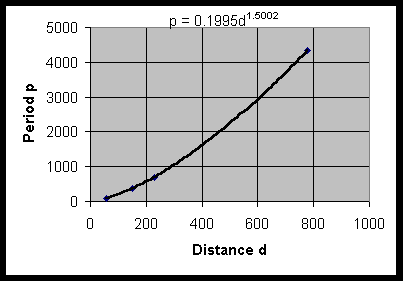
The power law expression relating the period of revolution (p) to the distance from the sun (d) is given by

where k and a are constants to be determined. We use the power law under Excel's trendline to best fit the data above. The graph below gives the best power law fit, showing k = 0.1995 and a = 1.5002. The power law clearly fits the data very well.

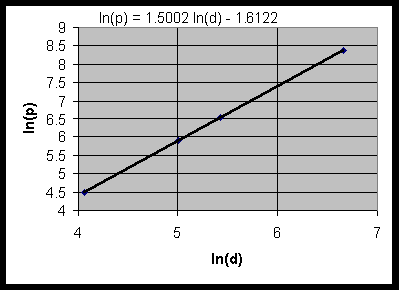
We saw that a straight line fits the logarithms of data that satisfy the power law, giving ln(p) = ln(k) + a ln(d) from the formula above. In the table above, take the logarithm of the Distance (ln(d)) and the logarithm of the Period (ln(p)). Here we'll use Excel's scatter plot and linear fit under trendline to see how this fits the data. The coefficient a agrees with the power a above, and exp(-1.6122) = 0.1994, which is almost the coefficient k found above. Again this straight line agrees extremely well with the data.

So now we use this power law to test the model against the other planets. Below is a table showing the calculated distance or period given either the distance or period of the planet along with the error from data taken from the Jet Propulsion Laboratory website (http://pds.jpl.nasa.gov/planets/welcome.htm)

Planet	Distance d	Period p	% Error
Venus	108.2	224.7	0
Saturn	1426	10,760	0.07
Uranus	2871	30739	0.19
Neptune	4497	60264	0.12
Pluto	5909	90,780	0.08

(The bold numbers are the calculated numbers, while the other number is the one given.)

References:

[1] E. K. Yeargers, R. W. Shonkwiler, and J. V. Herod, 1996, An Introduction to the Mathematics of Biology: with Computer Algebra Models, Birkhäser, Boston.

Problems:

1. Research has shown that the average number of mammalian species N on an island satisfies the equation

N = kA^1/3

where A is the area (in km²) of the island and k = 2.

a.Find the expected number of mammals on islands with 125 and 8000 km².

b. If you discovered an island had 32 different species of mammals, then, based on the formula above, approximately how large is the island?

c. Sketch a graph of the number of mammalian species on an island vs. the area of the island. Plot the points found in Parts a and b.

2. The Crew Classic rowing event on Mission Bay is held each year in spring. It can be shown that the times, t, of a particular race satisfy a power law with respect to the number of men, n, in the boat,

i.e. t = kn^a

You are given that the winning time for the eight man crew was exactly 6 min., while the winning time for the four man crew was 6min 28.8 sec (Remember to convert the seconds to decimal minutes.)

a.With the information given above find the value for k and a.

b. Use your answer from part a to determine likely winning times for the pairs (2 oarsmen) and singles (1 oarsman).

3. Data suggest that the lifetime of erythrocytes (red blood cells) for mammals satisfy an allometric model. The average lifetime for erythrocytes in a 70 kg man is 120 days. The average lifetime for erythrocytes in a 1.5 kg rabbit is 65 days. Use these data to find an allometric model for the lifetime of erythrocytes as a function of weight, i.e.,

Find the constants k and a. Use this model to determine the average lifetime for erythrocytes in a 20 kg dog. Also, determine the weight of an animal whose erythrocytes live for 100 days.

 4. In Gulliver's Travels, the Lilliputians decided to feed Gulliver 1728 times as much food as a Lilliputian ate. They reasoned that, since Gulliver was 12 times their height, his volume was 12³ = 1728 times the volume of a Lilliputian and so he required 1728 times the amount of food one of them ate. Why was their reasoning wrong? What is the correct answer?

5. Currently there is a debate on the importance of preserving large tracts of land to maintain biodiversity. Many of the arguments for setting aside large tracts are based on studies of biodiversity on islands. In this problem you apply the power rule to determine the number of species of herpetofauna (amphibians and reptiles) as a function of island area for the given Caribbean islands. You are given the following data [1]: