Math 121 - Calculus for Biology I Fall Semester, 2003 Linear - Worked Examples
	© 1999, All Rights Reserved, SDSU & Joseph M. Mahaffy San Diego State University -- This page last updated 12-Aug-02

 Linear - Worked Examples

Outline of Worked Examples:

1. Basic Examples
2. Graphing Lines
3. Intersection of Lines
4. Measurement Conversions
5. Word Problems

This section provides a number of worked examples that should help you work with and better understand straight lines. Straight lines are covered in standard algebra courses, so this should be review material. The problems below cover the basic concepts for finding equations of line, graphing lines, determining the points of intersection of two lines, conditions for two lines to be parallel or perpendicular, and several word problems that occur from biological models and measurement conversions.

Basic Examples

Example 1: Find the equation of a line with a slope of 2, passing through the point (3, -2). What is the y-intercept?

Solution: From the point slope form we obtain the equation:

This reduces to the equation

so the y-intercept is -8.

Example 2: Find the equation of a line passing through the points (-2, 1) and (3, -2).

Solution: The slope is given by

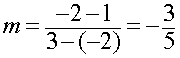
Thus, the point slope equation of the line is given by: y - y₀ = m(x - x₀)

 

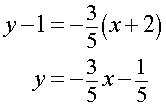
Note that using either point, (-2, 1) or (3, -2), will yield the same linear equation.

Parallel and Perpendicular Lines

Consider two lines given by the equations:

The two lines are parallel if the slopes are equal, so

and the y-intercepts are different. (If b₁ = b₂, then the lines are the same.) The two lines are perpendicular if the slopes are negative reciprocals of each other, that is

Example 3: Find the equation of the line perpendicular to the line 5x + 3y = 6, passing through the point (-2,1). Sketch a graph of both lines.

Solution: Converting this line (Line #1) to the slope intercept form, we obtain the equation:

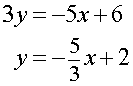
The slope of the perpendicular line is given by the negative reciprocal of that given above:

The point slope equation of the line (Line #2) is given by

Graphing Lines

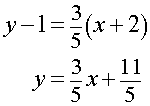
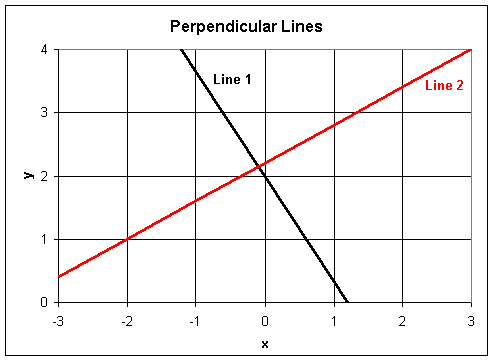
sourcecode for plotexample1c.java

Intersection of Lines

Example 4: Find the intersection of the line parallel to the line y = 2x passing through (1,-3) and the line given by the formula 3x + 2y = 5.

Solution: The first line is parallel to y = 2x, so has a slope m = 2. This line is found using the point slope equation:

The two lines intersect when both equations are satisfied simultaneously. The first line gives

This can be substituted into formula for the second line giving

or

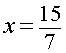
 Substituting the x value into the first line equation gives

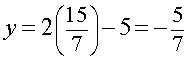
 Thus, the point of intersection is given by

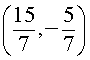
You can use the applet below to enter different values for m and b of two lines to find the point of intersection Use the Refresh button after you have put in the values for slope and intercept for the two lines

 source code for crosspoint.java

Measurement Conversions

Example 5: Find the weight of a 175 pound man in kilograms.

Solution: Since 1 kg = 2.2046 lb,

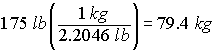
Example 6: Suppose a ball is thrown at a speed of 95 miles per hour. Find the speed of this ball in meters per second.

Solution: Since 1 mile = 1609.3 m and since there are 3600 sec in 1 hour,

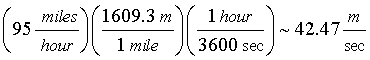
Use the conversion javascript to check your answers.

Word Problems

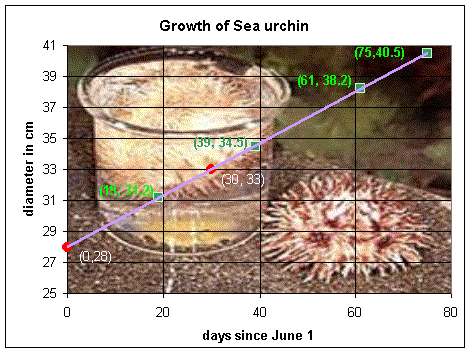
Example 7: The growth curve in the lecture notes shows that over a short period of time, using a straight line to estimate growth is quite reasonable. Suppose that a population of white sea urchins (Lytechinus pictus) has a mean diameter of 28 mm at the beginning of June (June 1) and 33 mm at the beginning of July (July 1). Estimate the mean diameter for the population of Lytechinus pictus on June 20, July 10, August 1, and August 15. Which estimates do you trust more and why?

Solution: Let the first day of June be defined as t = 0. Since there are thirty days in June, we can assume two data points, (0, 28), and (30, 33), where t corresponds to the number of days, and d corresponds to the mean diameter in mm. Assuming that there is a linear relationship between time, t, and diameter, d, we can find the equation of the line that passes through these two points. Calculating the slope:

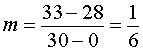
Using the point slope equation we obtain

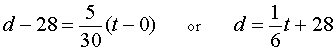
Note that b, the d-intercept, is essentially the initial diameter measurement. The slope m must then be the growth rate.

Using the above linear relationship, we can assume that the dates June 20, July 10, August 1, and August 15 correspond to the points (19, 31.2), (39, 34.5), (61, 38.2), and (75, 40.5), respectively. The estimate for June 20 is probably the most accurate because it falls between the two measurements actually taken. Also, recall that growth estimates are more accurate over shorter time intervals.

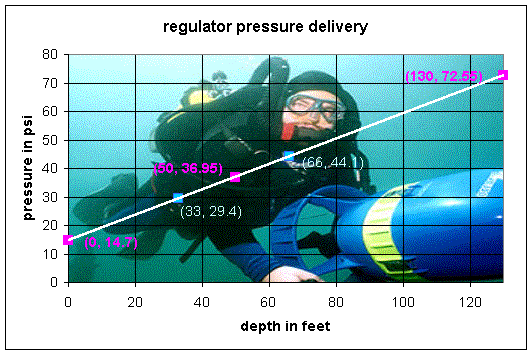
Example 8: The pressure of air delivered by the regulator to a Scuba diver varies linearly with the depth of the water. When the diver is at 33 ft, the regulator delivers 29.4 psi (pounds/square inch), while at 66 ft, the regulator delivers 44.1 psi. Find the pressure of air delivered at the surface (0 ft), at 50 ft, and at 130 ft (the maximum depth for recreational diving).

Solution: From the measurements taken, we can assume the two data points (33, 29.4), and (66, 44.1), where d corresponds to the depth in feet, and p corresponds to the regulator pressure in psi. Calculating the slope:

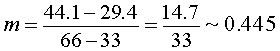
The equation of the line is then:

Therefore, using the linear relationship, we find that at the surface (d = 0), the air pressure is 14.7 psi. This calculation can be represented as a point, (0, 14.7). For depths of d = 50 ft and 130 ft, we obtain the points (50, 36.95), and (130, 72.55), respectively.