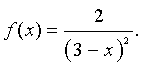
Lab J1 Solution (3 Versions)
This problem investigates the concept of a derivative from the geometric perspective of limiting secant lines going to a tangent line. It also allows you to explore the rules of differentiation using Maple.
Version 1:
a. Consider the function
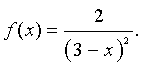
We want to investigate the derivative of f(x) at x = 2 by observing secant lines that pass through the points (2, f(2)) and (2 + h, f(2 + h)) for different values of h. The slope of the secant line is given by

and this line always passes through the point (2, f(2)). Find the equations of the 4 secant lines (in slope-intercept form) using h = 0.5, 0.2, 0.1, and 0.05. Use Excel to graph f(x) and the 4 secant lines for x in the interval [1, 2.95]. Limit the range, so that y is in the interval [-10, 20].
b. Find the general formula for the slope of the secant line through x = 2 and x = 2 + h. The slope of the tangent line is found by taking the slope of the secant line and letting h tend toward zero. This becomes the derivative of f(x) at x = 2. Find the derivative of f(x), f '(x), at x = 2. Find the equation of the tangent line at x = 2, then use Maple graph f(x) and the tangent line for x in the interval [0,3]. (Use the same limits on the range as in Part a.)
c. Differentiate the following functions using
Maple. You are just about to learn a collection of differentiation rules, so
you should be looking for patterns to help you in the future as we learn more
about derivatives.
|
i. f(x) = x2 + 3x -5
|
ii. f(x) = ( x2 + 3x -5)4
|
|
iii. f(x) =
e-3x
|
iv.f(x) =
ln(x+4)
|
Solution Version 1:
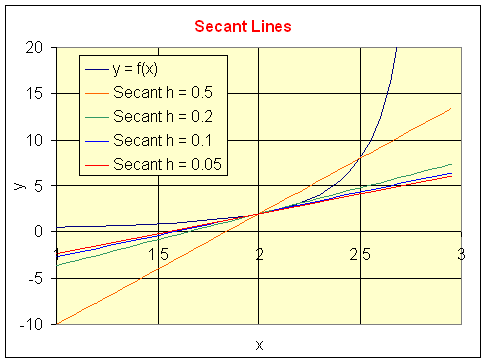
a. The equations of the secant
lines for f(x) at x = 2 are as follows:
1. When h = 0.5, then y = 12 x
- 22.
2. When h = 0.2, then y = 5.625 x
- 9.25.
3. When h = 0.1, then y = 4.691 x
- 7.383.
4. When h = 0.05, then y = 4.321 x
- 6.643.
The graph of these secant lines along with the function f(x)
are shown below.
b. With the help of Maple we find the slope of the general secant line through x = 2 and x = 2 + h of f(x), and it is given by:
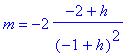
The limit as h approaches 0 in the above expression for the slope, m, gives m = 4, so the derivative of f(x) at x = 2 is f '(2) = 4. The equation of the tangent line at x = 2 is given by y = 4x - 6. The graph of the f(x) and its tangent line at x = 2 is shown below
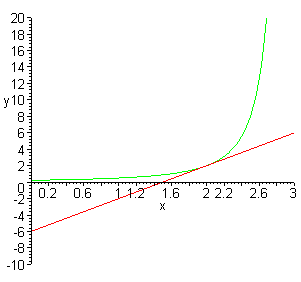
c. The derivatives for the expressions above are
(i) f '(x) = 2x - 3, which just uses the standard power rule learned in class.
(ii) f '(x) = 4(x2 + 3x -5)3(2x - 3), which show the exponent of the quantity in parentheses multiplying the quantity in parentheses with the power lower by one (like in the power rule), then multiplied by the derivative of the quantity inside the parentheses like in Part (i). This will be the chain rule developed later.
(iii) f '(x) = -3e-3x, which shows the derivative of the exponent of e multiplying the original function. This is the chain rule for the exponential function.
(iv) f '(x) = 1/(x + 4), which shows the derivative of the natural logarithm is one over the quantity of the which the logarithm is acting. (The chain rule will show the numerator is the derivative of this quantity, which is 1 in this case.)
Version 2:
a. Consider the function
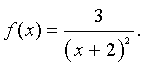
We want to investigate the derivative of f(x) at x = 2 by observing secant lines that pass through the points (2, f(2)) and (2 + h, f(2 + h)) for different values of h. The slope of the secant line is given by

and this line always passes through the point (2, f(2)). Find the equations of the 4 secant lines (in slope-intercept form) using h = 0.5, 0.2, 0.1, and 0.05. Use Excel to graph f(x) and the 4 secant lines for x in the interval [1, 2.95]. Limit the range, so that y is in the interval [-10, 20].
b. Find the general formula for the slope of the secant line through x = 2 and x = 2 + h. The slope of the tangent line is found by taking the slope of the secant line and letting h tend toward zero. This becomes the derivative of f(x) at x = 2. Find the derivative of f(x), f '(x), at x = 2. Find the equation of the tangent line at x = 2, then use Maple graph f(x) and the tangent line for x in the interval [0,3]. (Use the same limits on the range as in Part a.)
c. Differentiate
the following functions using Maple. You are just about to learn a collection
of differentiation rules, so you should be looking for patterns to help you
in the future as we learn more about derivatives.
|
i. f(x) = x2 - 5x + 4
|
ii. f(x) = ( x2 - 5x +
4)5
|
|
iii. f(x) =
e-2x
|
iv.
f(x) = ln(x+5)
|
Solution Version 2:
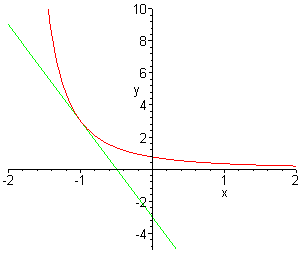
a. The equations of the secant
lines for f(x) at x = -1 are as follows:
1. When h = -0.5, then y = -18 x
- 15.
2. When h = -0.2, then y = -8.4375 x
- 5.4375.
3. When h = -0.1, then y = -7.037 x
- 4.037.
4. When h = -0.05, then y = -6.482 x
- 3.482.
The graph of these secant lines along with the function f(x)
are shown below.
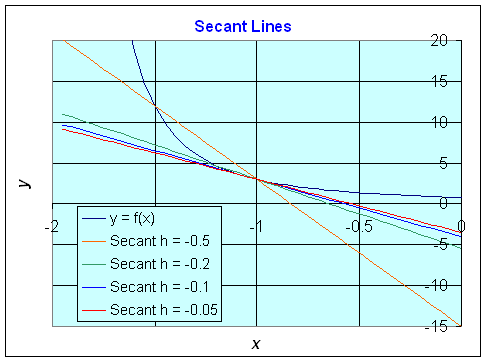
b. With the help of Maple we find the slope of the general secant line through x = -1 and x = -1 + h of f(x), and it is given by:
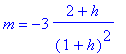
The limit as h approaches 0 in the above expression for the slope, m, gives m = -6, so the derivative of f(x) at x = -1 is f '(-1) = -6. The equation of the tangent line at x = -1 is given by y = -6x - 3. The graph of the f(x) and its tangent line at x = -1 is shown below
c. The derivatives for the expressions above are
(i) f '(x) = 2x - 5, which just uses the standard power rule learned in class.
(ii) f '(x) = 5(x2 - 5x + 4)4(2x - 5), which show the exponent of the quantity in parentheses multiplying the quantity in parentheses with the power lower by one (like in the power rule), then multiplied by the derivative of the quantity inside the parentheses like in Part (i). This will be the chain rule developed later.
(iii) f '(x) = -2e-2x, which shows the derivative of the exponent of e multiplying the original function. This is the chain rule for the exponential function.
(iv) f '(x) = 1/(x + 5), which shows the derivative of the natural logarithm is one over the quantity of the which the logarithm is acting. (The chain rule will show the numerator is the derivative of this quantity, which is 1 in this case.)
Version 3:
a. Consider the function
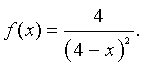
We want to investigate the derivative of f(x) at x = 3 by observing secant lines that pass through the points (3, f(3)) and (3 + h, f(3 + h)) for different values of h. The slope of the secant line is given by

and this line always passes through the point (3, f(3)). Find the equations of the 4 secant lines (in slope-intercept form) using h = 0.5, 0.2, 0.1, and 0.05. Use Excel to graph f(x) and the 4 secant lines for x in the interval [2, 3.95]. Limit the range, so that y is in the interval [-10, 30].
b. Find the general formula for the slope of the secant line through x = 3 and x = 3 + h. The slope of the tangent line is found by taking the slope of the secant line and letting h tend toward zero. This becomes the derivative of f(x) at x = 3. Find the derivative of f(x), f '(x), at x = 3. Find the equation of the tangent line at x = 3, then use Maple graph f(x) and the tangent line for x in the interval [0,4]. (Use the same limits on the range as in Part a.)
c. Differentiate the following functions using Maple. You are just about to learn a collection of differentiation rules, so you should be looking for patterns to help you in the future as we learn more about derivatives.
|
i. f(x) = x2 + 6x -7
|
ii. f(x) = ( x2 + 6x -7)6
|
|
iii. f(x) =
e4x
|
iv.f(x) =
ln(x-2)
|
Solution Version 3:
a. The equations of the secant
lines for f(x) at x = 3 are as follows:
1. When h = 0.5, then y = 24 x
- 68.
2. When h = 0.2, then y = 11.25 x
- 29.75.
3. When h = 0.1, then y = 9.383 x
- 24.15.
4. When h = 0.05, then y = 8.643 x
- 21.93.
The graph of these secant lines along with the function f(x)
are shown below.
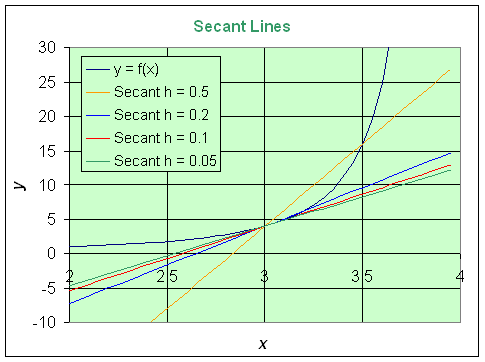
b. With the help of Maple we find the slope of the general secant line through x = 3 and x = 3 + h of f(x), and it is given by:
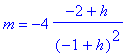
The limit as h approaches 0 in the above expression for the slope, m, gives m = 8, so the derivative of f(x) at x = 3 is f '(3) = 8. The equation of the tangent line at x = 3 is given by y = 8x - 20. The graph of the f(x) and its tangent line at x = 3 is shown below
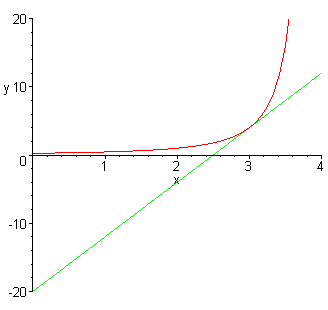
c. The derivatives for the expressions above are
(i) f '(x) = 2x + 6, which just uses the standard power rule learned in class.
(ii) f '(x) = 6(x2 + 6x -7)5(2x + 6), which show the exponent of the quantity in parentheses multiplying the quantity in parentheses with the power lower by one (like in the power rule), then multiplied by the derivative of the quantity inside the parentheses like in Part (i). This will be the chain rule developed later.
(iii) f '(x) = 4e4x, which shows the derivative of the exponent of e multiplying the original function. This is the chain rule for the exponential function.
(iv) f '(x) = 1/(x - 2), which shows the derivative of the natural logarithm is one over the quantity of the which the logarithm is acting. (The chain rule will show the numerator is the derivative of this quantity, which is 1 in this case.)