| Joseph M. Mahaffy |
 |
| Math 124: Calculus for the Life Sciences | Fall 2016 |
Computer Lab Help Extra
This page is designed to provide helpful information about the special laboratory questions. This is a collection of Computer Lab problems that you can work for extra credit. The problems draw from a collection of computer labs from the old Math 121 and 122 courses, which were not used this semester. You should ignore any part that asks you create something for a lab report, as these are to be done entirely in WeBWorK. Obviously, you will need to do many of the preliminary computer computations, which would lead to the graphs needed in these problems. However, you only work the WeBWorK problems. These problems will be due just before finals week begins. Each problem is worth 20 bonus points, which is added directly to your cumulative Lab score. You are allowed 15 attempts on each problem.
There are 5 problems selected from a range of areas. The first problem explores fitting plankton blooms in the Salton Sea. This problem fits a 4th order polynomial through the logarithm of some data, then you explore the extrema using techniques of Calculus. The second problem considers a discrete model for the spread of influenza. This SIR model is popular in epidemiology, and you will learn the importance of different treatment regimes. The third problem explores the fitting of 4 trigonometric functions to data for some tides in San Diego. Again techniques from Calculus, using Maple helps find high and low tides. The fourth problem considers the dangers of CO in a room. This problem uses both analytic and numerical methods to find dangerous levels of this gas. The last problem studies the classical Lotka-Volterra predator prey model. You extend your Euler techniques to this two-dimensional model. The special instructions below are taken directly from the help pages from before, so some of the instructions pertain to the formal lab report, which you can ignore.
Problem 1: This problem is similar though a little more difficult than the Lab on the O2 consumption of kissing bugs or the one above on the monthly rhythms of body temperature for females. You start this problem by simply graphing the data and applying the log scale option to the vertical axis. Recall that to change the graph to having a Logarithmic scale, you can go to the Main menu and select Insert, then choose the Layout tab, under which you select Axes. From here you select the Primary Vertical Axis and choose More Primary Vertical Axis Options. This opens a box of Axis Options, where you can check the box for Logarithmic scale. It should be noted that this long progress can be simplified by going directly to the graph. You move the cursor until a box appears that says Vertical (Value) Axis, then you Right Click and the box of options to Format Axis appears, where you simply check the box Logarithmic scale. It probably looks best if you plot the data as points connected by straight lines, which is the fourth choice of the XY-scatter plot graphs.
In Part b, you take the log of the data and plot it. You simply apply Excel's Trendline find the best fit to the data with a 4th order polynomial. (Do NOT forget to change the Excel Trendline equation to scientific notation and obtain 5-6 significant figures by choosing 4-5 decimal places!) For Part c, you will be able to differentiate this polynomial either with Maple or by hand. Since the derivative is a cubic equation, you will probably need Maple to find when the derivative of this polynomial is zero. This is another application with real data, where you find maxima and minima of the data using polynomial fits (though a polynomial is not likely to be the best choice in this case as populations fluctuate annually). For the most part, this problem is very much like the "kissing bug" problem with a bit more data and a higher order polynomial.
Problem 2: This question expands the single population modeling concept as illustrated in earlier labs to a system of discrete dynamical equations. Data are provided from a flu season tracked by the Center for Disease Control (CDC). The Susceptible-Infected-Recovered (SIR) model is used, and the simulation is assumed to be over a closed population that doesn't grow. Thus, the model is assumed to examine a well-mixed population with a constant size, which is given. This easily allows you to eliminate one of the variables in the SIR model and reduce our modeling effort to the study of only the infected (In) and susceptible (Sn) individuals in the sample population. The data only tracks the infected individuals, so we only fit our data to this class.
Begin by copying the data from the CDC into Columns A and B on an Excel Spreadsheet. Create named parameters, b, g, and N on the spreadsheet (say in Columns G and H) to use in the model with the initial values given in the Lab problem. In Columns C and D we insert our model., starting with the initial populations of susceptible (S0) and infected (I0) individuals. In the cells below the initial populations, you insert the equations given in the Lab problem using the named parameters. In Column E, you find the square error between the CDC data on infected individuals and the numbers given by the model. As we have done before, you sum the square error between the model and the data using Excel's Solver changing the parameters b and g. Note that you are only fitting the population of infected individuals to the data, but you use the information about the susceptible individuals to determine the total number of people getting the flu over the season.
The remainder of the problem has you simulate the model with changes in S0, b, or g, to reflect treatment plans of vaccination, education/isolation, or antiviral medicine. You simply change the appropriate parameter, then simulate the model as you did in the first part of the problem. You will report quantitative information that you gather and discuss something about these different strategies and their efficacy.
Problem 3: This problem asks you to repeat some of the calculations required to produce the graphs that appear in the derivative of the trigonometric functions section on tides. Much of the most difficult work has already been done for you and is provided by a downloadable Excel worksheet. This sheet contains a cover page with instructions to read about the Tide problem and one sheet for each of the 12 months in 2009. These sheets summarize all the high and low tides for each month gathered from the NOAA website on tide tables.
You begin by finding the appropriate month for your particular lab. The particular worksheet has the time in hours from the beginning of the month, the hours converted to days, and the height in feet of all the high and low tides. To the right you'll find a table of parameter values. You will begin by naming all the parameters in the usual way (Insert - Name - Create). For this problem you will keep the force periods Pi (labeled p1t, p2t, p3t, and p4t) the same. The initial values are provided for the parameters Ai and fi. A0 represent the average height of the tides over the entire month; however, a reasonable approximation for the initial value of A0 is 3. The next step is to enter the formula given to you in the problem, using these parameters, in Column D and pull it down to the end of the month. For the t-values use the values in Column A. In Column E, you compute the square error, and sum this at the bottom of the column.
As we have done before, we use Excel's Solver to minimize the sum of square errors. When you are in Solver for Excel 2010, you need to uncheck the box labeled: Make Unconstrained Variables Non-negative. In this problem you allow solver to change the Variable Parameters in Column L. You should implement Excel's Solver twice to guarantee convergence of such a large set of parameters.
Important: The next step is to convert the parameters of amplitude, Ai, and principle phase shift, fi, to a unique set. If your value of Ai is negative, then you need to shift your phase by half a period, remembering that the specific periods are set by each force with period, Pi. Also, you need to adjust all phases, fi, so that you select 0 < fi < Pi. This may require that you add or subtract an integer multiple of the period. It is recommended that after you make these adjustments that you apply Excel's Solver again twice. There should be no change in the sum of square errors and the magnitudes of the amplitudes should be unchanged.
Create a graph for the week requested by first plotting the data for that week. In this case, use the values in Column B on the x-axis. Do not forget to account for the fact that the first of the month goes from 0-24 hours, so a particular date, say June 8, uses the times between 7 and 8. For the model of the tides, you create one column like Column A, another like Column B, and another like Column D with the model depending on Column A. Start with the appropriate time for your particular week (if it starts on June 8, then start with t = 24*7 = 168) and add 0.5 hours for each time step until you reach the end of the week (which is June 15 for our example, so t = 24*14 = 336, which is 337 data points, not the usual 50 data points). Add this smooth curve over the data points from the NOAA data to get your graph of the week.
For your graph of a day, you do the same process as you did for the graph of a week, but you use time steps of only 0.25 hours. You include the data also in this graph along with appropriate labeling.
To find the minima and maxima, you are going to use Maple. You enter the function in Maple from the numbers on your Excel spreadsheet. Use the information on the spreadsheet or the graph to narrow the range of search for the key values (in hours) of the highest and lowest tides (or any other high or low tide), then proceed as you have always done to differentiate your function for the height of the tides and set the derivative equal to zero (diff and fsolve commands). Because of the difference in times between the tides you can use a 2-4 hour spread of times around your estimate of a high or low tide to allow Maple's fsolve to find the precise timing of the model relative extrema. These times can be compared to the ones provided in Column A. The remainder of the questions should follow readily from the answers provided above.
Problem 4: This lab asks you to use the Improved Euler's method, which is a numerical method that is significantly better than the Euler's method. (You can also go to the notes on Numerical Differential Equations.) Below is information for using this technique:
The numerical techniques given by Euler's Method and Improved Euler's Method are used to approximate solutions to differential equations using a simple discrete algorithm. For each method you will be given a differential equation of the form:
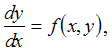
a step size given by h and an initial condition y(0) = y0. Given the fact that both numerical methods are discrete formula much like the discrete dynamical models from earlier this semester, it is easy to work with Euler's and Improved Euler's method in Excel.
We will begin by constructing a column for xn, a column
for yn and then
finally a column for f(xn,yn).
In the first row of our Excel sheet we want to input the
initial x = x0
and y = y0
values. In the f(xn,yn)
column we want to calculate the value of the differential
equation at x0
and y0.
Example: If
we had the problem:
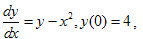
then we would fill in the first row of our Excel sheet as follows:
| x(n) | y(n) | f(x(n), y(n)) |
| 0 | 4 | = B2 - A2^2 |
Euler's Method
We are now ready to set up the rest of the discrete model for Euler's Method. Geometrically, Euler's method starts at the initial point , y0, then it uses the direction of the derivative to step a distance, h, and project the next guess at where the solution should be. It proceeds in a similar manner at each step moving a distance forward h in the x direction and using the derivative at the new position to move in a straight line direction to the next y value. Thus, in the xn column we want to produce x values the go up by our given step size h. (In the following, you can either create a named variable h, or insert your value of h. The former gives you a more general Euler's method to continue for varying the stepsize.) So in the cell below the initial x value we type in the formula '=A2+h'. We have now created the x1 term. Euler's Method is given by the equation
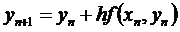
So in the cell below the initial y values we
type in the formula: '=B2+h*C2'.
Remember that the B column in this example represents our
y
values and the C column represents the value of our
differential equation. In the final column for f(xn,yn)
(the derivative or direction of the solution at (xn,yn)),
we want to once again calculate the value of the
differential equation for xn and yn so we use
the same formula we used in cell C2. We are now
ready to simulate Euler's Formula for as many steps as we
would like. We simply highlight all three cells (A2,
B2, and C2 in our example) and click and drag down until
we've reached the final xn
value.
| A | B | C | |
| 1 | x(n) | y(n) | f(x(n), y(n)) |
| 2 | 0 | 4 | = B2 - A2^2 |
| 3 | =A2 + h | =B2 + h*C2 | = B3 - A3^2 |
| : | : | : | : |
Improved Euler's Method
The Improved Euler's Method uses an intermediate step to improve the accuracy of the approximation (significantly). In this case, instead of fitting a straight line in the direction of the solution, it uses a mathematical trick to fit the best quadratic in the direction of the solution. Computationally, this means that we need to do one more function evaluation to get a much better numerical solution. This is accomplished in Excel by adding two more columns: one that has the Euler solution ye and another column that gives the improved update to the derivative using the updated time and Euler's solution. The first three columns of this method are constructed in a similar way as the normal Euler's formula. In the fourth column we input the normal Euler's model, i.e., '=B2+h*C2'. Notice that instead of putting this formula in the cell just below the last yn value we are now putting it in its own column. In the fifth column we insert the improved calculation for the derivative given by f(xn+h, ye). The new value for y in the second column below this row uses an average of the Euler approximation of the derivative and the updated Improved Euler approximation of the derivative. The new updating function to approximate the solution of the differential equation using the Improved Euler's Method in the cell below the yn term is given by the formula:
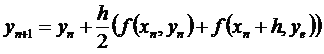
This formula uses the same idea as Euler's Formula, except instead of simply moving a step in the direction of the derivative, a correction is made while moving that step to account for nonlinear changes in the function f. In Excel the code in the cell B3 (just below the initial y value) would be '=B2+(h/2)*(C2+(D2-(A2+h)^2)). Notice that the last piece of the formula (D2-(A2+h)^2) is simply f(xn+h, ye). The rest of the code is the same and we can then click and drag the row to produce results to any xn we would like:
| A | B | C | D | E | |
| 1 | x(n) | y(n) | f(x(n), y(n)) | ye | f(x(n)+h, ye) |
| 2 | 0 | 4 | = B2 - A2^2 | = B2 + h C2 | = D2 - (A2+h)^2 |
| 3 | =A2 + h | =B2 + (h/2)*(C2 + E2) | = B3 - A3^2 | = B3 + h C3 | = D3 - (A3+h)^2 |
| : | : | : | : | : | : |
Its important to
note that the subscript when the formula has the two
subscripts n+1
and n, such
as yn =yn + hf(xn,yn),
that they designate which value to use. In this
case n
represents the previous value, so when determining the
value of y1
then n+1 = 1
and n = 0,
so y1
=y0
+ hf(x0,y0).
Thus, we obtain the new values for the updating function
from the row above the new row.
This specific problem is very much like the lake pollution problems that you have studied in class. The set up of the differential equation model follows techniques from the notes on Linear Differential Equations. You may also want to consult the discussion of the lake pollution problem at the beginning of the numerical section for differential equations. The techniques for numerically solving this problem are shown above.
Problem 5: This question uses Excel's Solver like you have done several times this semester. This is a slightly more complicated application. The data is provided in your problem, and an Excel sheet is provided to aid your analysis. Data from your problem is entered in Columns B and C. You enter the appropriate guesses for the parameters in Cells J1:J6. Name your variables, then simulate the model with Euler's method in Columns L. M, and N.
In Columns D and E, you place the values from the cells generated in the Euler simulation. Be sure to take only the values from the cells with the same corresponding day. In Columns F and G, you insert the values for the square errors between Columns B and D and Columns C and E. Sum all these squares errors, then have Excel's Solver find the minimum with respect to the parameters in Column J. From here the techniques are similar to the ones you've done before.