1. Predator-Prey
2. Lotka-Volterra model
3. Equilibrium Analysis
4. Linear Analysis
5. Periodic Solutions
6. Integrating about the Periodic Orbits
7. Fitting the Parameters to the Model
8. Model of Fishing
9. Equilibria of the Fishing Model
10. Worked Examples
11. References

The previous section developed techniques for the qualitative analysis of nonlinear differential equations, where the differential equation contained a single unknown variable. The techniques allowed the reader to understand the behavior of mathematical models without actually solving the differential equations. This section looks at a predator-prey model where two species are involved. Thus, the differential equations describing the population dynamics must have two unknown variables, creating a system of differential equations. This system of differential equations cannot be solved exactly, so either numerical or qualitative methods need to be employed. One particularly interesting feature of this system is that the equilibrium analysis can give valuable ecological information, showing the use of pesticides is fundamentally a bad idea.

In this section, we develop the mathematical models for two species that are intertwined in a predator-prey or host-parasite relationship. As we have done before, the differential equations will be analyzed to find equilibria, linearize about the equilibria for stability analysis, show existence of periodic solutions, and perform some parameter identification to match the model to data. These techniques allow the reader to examine a wide range of models that have been developed in biology and other fields.

Predator-Prey

Our study begins with a classical example shown in many ecological textbooks, the population dynamics of a simple predator-prey system. Most mammalian predators rely on a variety of prey, which complicates mathematical modeling; however, a few predators have become highly specialized and seek almost exclusively a single prey species. An example of this simplified predator-prey interaction is seen in Canadian northern forests, where the populations of the lynx and the snowshoe hare are intertwined in a life and death struggle.

One reason that this particular system has been so extensively studied is that the Hudson Bay company kept careful records of all furs from the early 1800s into the 1900s. It is often assumed that the furs are representative of the populations in the wild because of the trapping intensity and trapping techniques, so these data can be used to represent the relative populations of the lynx and hares in the wild. The records for the furs collected by the Hudson Bay company showed distinct oscillations (approximately 12 year periods), suggesting that these species caused almost periodic fluctuations of each other's populations. Below is a graph of some of the fur data from the records of the Hudson Bay company.

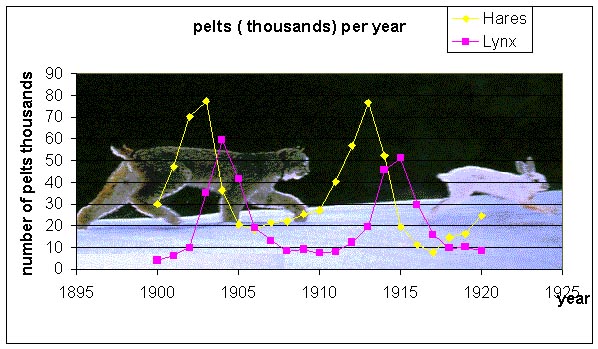
We would like to create a mathematical model that explains these population fluctuations. Ecologists have predicted that in a simple predator-prey system that a rise in prey population is followed (with a lag) by a rise in the predator population. When the predator population is sufficiently high, then the prey population begins dropping. After the prey population falls, then the predator population falls, which allows the prey population to recover and completes one cycle of this interaction. Thus, we see that qualitatively oscillations occur. Can a mathematical model predict this? What causes cycles to slow or speed up? What affects the amplitude of the oscillation or do you expect to see the oscillations damp to a stable equilibrium? The models tend to ignore factors like climate and other complicating factors. How significant are these?

The Predator-Prey Model (Lotka-Volterra)

The mathematical predator-prey model and its cyclical nature was published in 1920 by Alfred Lotka, an American biologist and actuary, and developed throughout the 1920s, as an extension of Lotka's work in autocatalysis in chemical reactions. Lotka is regarded as the originator of many useful theories of stable populations, and his publications have been accepted as the basis for much subsequent work, including the Logistic model studied previously. Subsequent to these extensive publications, Vito Volterra in 1925 proposed the same model as an explanation of data from some fish studies of his son-in-law Humberto D'Ancona on the fishing industry in Italy (see below). Several of the two species predator-prey and competition models are called Lotka-Volterra Models, to distinguish them from other Lotka models in different fields of interest. Their models were natural extensions of the Verhulst or logistic model that we studied in earlier sections. This work is presented in most basic ecology textbooks and has many references on the web. One good study is shown in the work of M. Beals, L. Gross, and S. Harrell in their web modules from the University of Tennessee. Below we present the basic assumptions needed to create the classical Lotka-Volterra predator-prey model for the dynamics of the populations of a predator and its prey species.

Let H(t) be the population of snowshoe hares and L(t) be the population of lynx. As we have done before, we want to develop a mathematical model based on the growth rates for the populations. That is, the rate of change in a population is equal to the net increase (births) into the population minus the net decrease (deaths) of the population. We begin by applying this to the population of snowshoe hares. The rate of change of the hare population is dH/dt. The primary growth in the hare population is Malthusian, so this says that the population grows in proportion to its own population or a₁H(t). We will make the simplifying assumption that the primary loss of hares is due to predation by lynx. Predation is often modeled by assuming random contact between the species in proportion to their populations with a fixed percentage of those contacts resulting in death of the prey species. Mathematically, this is given by a negative term, -a₂H(t)L(t). Clearly, if there are other major predators or if the lynx population is low such that starvation due to overcrowding dominates the death rate, then alternative death terms would be more appropriate. Combining these terms, we obtain the growth model for the hare population:

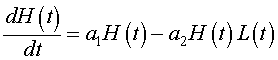
Next we examine the population dynamics of the lynx. The rate of change of the lynx population is dL/dt. The primary growth for the lynx population depends on sufficient food for raising lynx kittens, which implies an adequate source of nutrients from predation on hares. Thus, the growth of the lynx population is similar to the death rate for the hare population with a different constant of proportionality. Mathematically, it follows that the growth of the lynx population can be written, b₂H(t)L(t). The loss of lynx is presumed to be a type of reverse Malthusian growth. That is, in the absence of hares, the lynx population declines in proportion to their own population, which mathematically is given by the negative modeling term, -b₁L(t). Clearly, if the lynx diet used other animals or crowding factors from other predators and lynx were taken into account, then these terms would have to be significantly modified. The growth model for the lynx population combines these terms above to give the following:

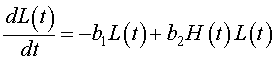
Clearly, the growth equations above are caricatures of the true complicated dynamics of these two animals. The model ignores the role of climate variation and the interactions of other species, including human disturbance. Other significant factors that are ignored in this modeling effort are the ages of the animals and the spatial distribution. However, we would like to see if this basic model can give a qualitatively similar picture to the dynamics that are observed in the Hudson Bay company furs that are graphed above. The Lotka-Volterra model is given by the system composed of the two differential equations written above. Note that these differential equations are intertwined into a system of differential equations with each growth model depending on the unknown variable (population) of the other.

Equilibrium Analysis

As in previous analyses of dynamical systems, the first step to a qualitative analysis is finding the equilibria of the model. Equilibrium solutions are ones that do not change in time, so the derivatives are equal to zero. Thus, for the predator prey model above, we set

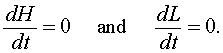
This results in a system of nonlinear algebraic equations to solve. If we let H_e and L_e be the equilibrium solutions for the snowshoe hare and lynx populations respectively, then the system of algebraic equations that we need to solve is given by

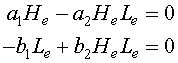
In general, the solution of a system of nonlinear equations can be very difficult, but this case is relatively simple to solve using standard tools from algebra. These two equations can be factored, which aids in finding the solution. The first equation can be written

which implies that either H_e = 0 or a₁ - a₂L_e = 0. Thus, we have possible equilibria at

Similarly, the second equation can be factored to give

which implies that either L_e = 0 or -b₁ + b₂H_e = 0. Thus, we have possible equilibria at

The simultaneous solution of these two equations shows that when H_e = 0, then L_e = 0, which gives rise to the trivial solution (extinction of both species)

The other equilibrium is given by

Unfortunately, the equilibria do not help explain the oscillatory behavior of the data reflected in the lynx and snowshoe hare data. We need information about the stability of these equilibria and further numerical and qualitative analysis techniques before we can demonstrate that this is an appropriate model. We perform a linear analysis and integrate about the equilibria, then return to the original example of Vito Volterra to show how even the equilibrium analysis of this simple model can explain some important ideas in population dynamics of a predator prey system.

Linear Analysis

As we showed in our previous work, a system of differential equations is linearized about its equilibria by finding the Jacobian of the vector function of the nonlinear system of differential equations. For the predator-prey model given above, the Jacobian matrix is given by

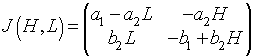
When this is evaluated about the equilibrium (H_e, L_e) = (0, 0), the Jacobian matrix is

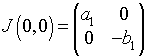
This has the eigenvalues and associated eigenvectors,

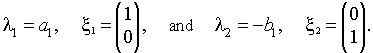
This shows that the equilibrium (0, 0) is a saddle node with solutions exponentially growing along the H-axis and decaying along the L-axis. The linear solution has the form

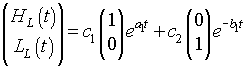
When this is evaluated about the equilibrium (H_e, L_e) = (b₁/b₂, a₁/a₂), the Jacobian matrix is

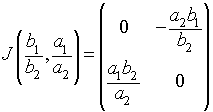
This has the purely imaginary eigenvalues,

This shows that the equilibrium (b₁/b₂, a₁/a₂) is a center, which suggests that the solution cycles around as we suspected for the predator-prey model. The linear solution can be shown to satisfy

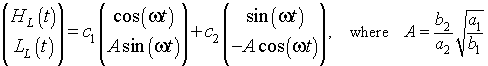
This produces a structurally unstable model. The model is structurally unstable because small perturbations from the nonlinear terms could result in the solution either spiraling toward or away from the equilibirum.

Periodic Solutions

This model can be shown to have limit cycles for all positive initial conditions. The technique uses a simple integration following separation of variables of the differential equation found by dividing the two equations, i.e.,

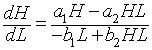
The solution of this equation has the implicit solution

We need to demonstrate that this implicit solution has periodic solutions. Define the two sides of the implicit solution by

For the equation F_H(H), we see that there is a vertical asymptote at H = 0. Differentiating this function gives

This has a minimum at the equilibrium H_e = b₁/b₂, then increases monotonically toward infinity. A similar argument shows that F_L(L) has a maximum at L_e = a₁/a₂, while the function begins with F_L(0) = 0, then following the maximum asymptotically approaches 0. Graphs of these functions are shown below using the best model fit for the lynx-hare data.

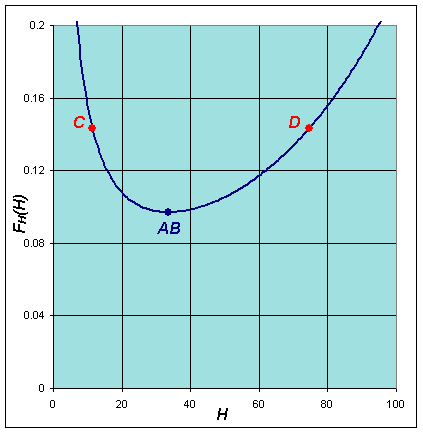
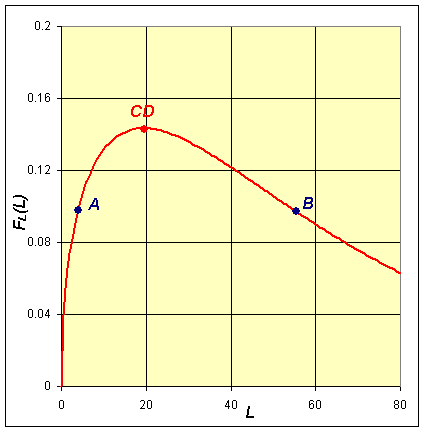
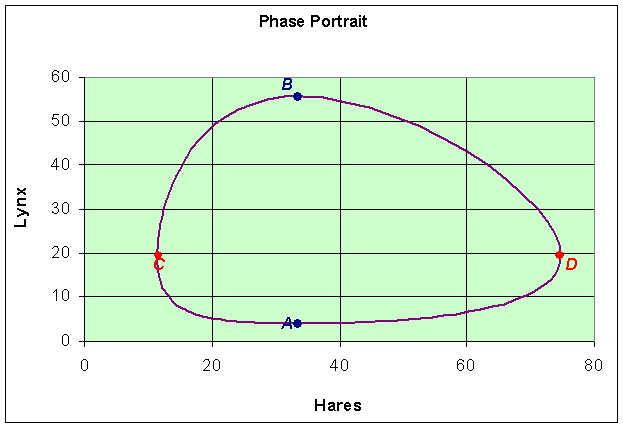
The implicit solution shows that these functions are equal (with F_L(L) shifting depending on the integration constant). Based on the analysis and the graphs, then they can be equal only on the range between the minimum of F_H(H) and the maximum of F_L(L). When F_H(H) is at the minimum, then F_L(L) has two distinct possible values. These two values correspond to the high and low values of the lynx population in the periodic orbit. (See the points marked A and B below and on the graphs above.) As we consider larger values of F_H(H), there are two values of H corresponding to each value of F_H(H), and each of these two values of H are paired with two values of L until we reach the maximum of F_L(L). At the maximum of F_L(L), L_e = a₁/a₂ and F_H(H) has two distinct possible values, which correspond to the high and low values of the hare population in the periodic orbit. (See the points marked C and D below and on the graphs above.) It follows that there must be a periodic orbit.

Integrating about the Periodic Orbits

With the knowledge that the orbits are periodic, we can ask about the average value of the solution. Suppose that a particular orbit has a period of T. The average population of hares for one period is given by the integral

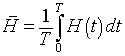
and the lynx average satisfies

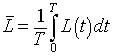
Consider the differential equation for the hare population. If we divide by H(t), then integrate around one period we have the following:

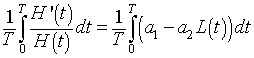
Fitting the Parameters to the Model

As we did in the competition models before, we would like to find the least squares best fit to the data from the Hudson Bay company on the pelts of the lynx and hares. Below we present the table of data.

To perform the least squares best fit to the data using the predator-prey model, we need good estimates of the parameters. The parameters that are varied for this model are the initial conditions, H(0) and L(0), and all of the growth and death rate constants, a₁, a₂, b₁, and b₂. The initial choices for the initial conditions come directly from the data, so we take

H(0) = 30 and L(0) = 4.

To find the rate constants, we use a number of the relations derived above. Recall that the integral about one period of the model gives the values of the equilibria. So if we average the data between two maxima or minima, then we should obtain a reasonable estimate of the equilibria for these data. Averaging the data between 1903 and 1913 (omitting the last year to not bias the maximum) for the hares and the data from 1904 to 1915 (again omitting 1915), we have the following equilibrium estimates

H_e = b₁/b₂ = 34.6 and L_e = a₁/a₂ = 22.1.

The data indicate that the period of the solution should be around 12 years so from the eigenvalues of the equilibrium, we can get an estimate of the frequency

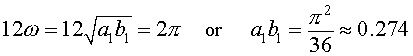
Note that this value is likely to be a little low because the period of oscillation generally increases as you move away from the equilibrium. This estimate is near the equilibrium, so using the higher value of the period, 12, generated a distance away from the equilibrium indicates that the product a₁b₁ is too low. From the model, we would expect that when the predator population is very low, then the prey population is undergoing Malthusian growth, so provides some estimate of the growth parameter a₁. From the graph of the data, we see a low in lynx around 1910. At this time we see the hare population growing rapidly. If we use the population of 27.1 in 1910 and 40.3 in 1911, then assuming a Malthusian growth model of the form

we obtain the estimate

a₁ =ln(40.3/27.1) = 0.397.

This estimate is clearly a little low because of the effects of predation that are ignored. Similarly, we examine the data for low populations of hares to find the exponential decline of the lynx population. We see that the steepest decline of the of the lynx population occurs between 1905 and 1906 with populations of 41.7 and 19, respectively. If we consider a decaying solution of the form

then the data gives the following estimate

b₁ = ln(41.7/19) = 0.786.

Because of the growth term, the estimate above is should be low. Note that these estimates are reasonably consistent.

Combining the information above, we obtain the following initial estimates for the parameters

a₁ = 0.4, a₂ = 0.018, b₁ = 0.8, and b₂ = 0.023.

With these estimates on the parameters, we can use MatLab to find the least squares best fit of the model to the data. The MatLab code is given below as a single function.

with the sum of squares error being

J = 593.28.

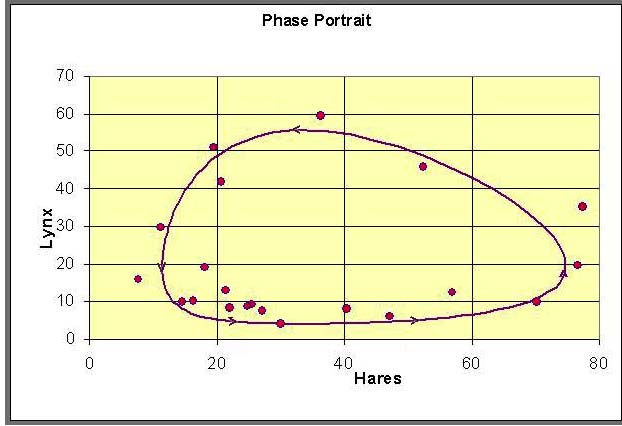
We can graph the data and the model using these parameters and obtain the following graph of the populations of lynx and hares as functions of the year:

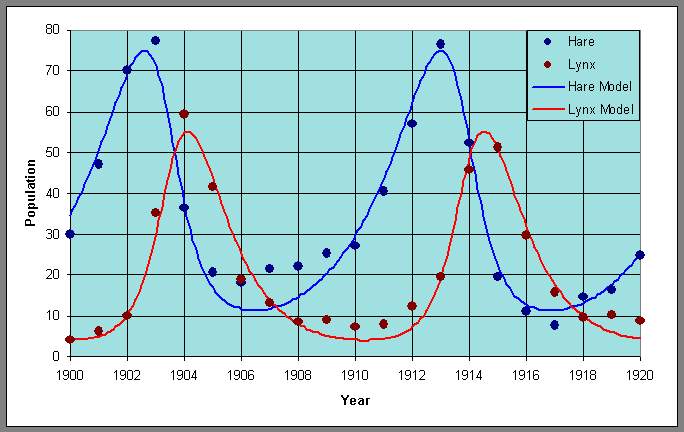
Similarly, we can plot the data with the periodic orbit to obtain a phase portrait.

Model of Fishing

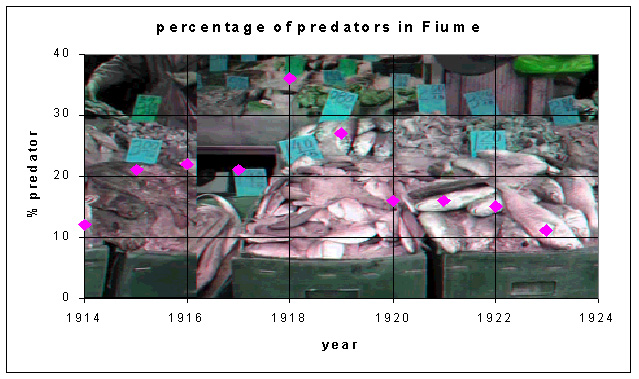
Humberto D'Ancona was an Italian biologist who, in 1924, completed a statistical study of fish populations in the Adriadic Sea. He observed that, during the time of reduced fishing in World War I, his populations showed an increasing percentage of predator fish, especially sharks and skates (or a decrease of prey fish). This increase in population of the predator fish declined after the war. Vito Volterra, his father-in-law, was an Italian mathematician who had recently retired, and D'Ancona asked Volterra if there was a mathematical model which could explain this observed relative change in the populations of fish species. Within a couple of months, Volterra produced a series of mathematical models for the interaction of two or more species. Below is a table showing his data with a graph.Why should World War I affect the relative frequency of fish in Italian ports?

Percentages of predators in the Fiume fish catch

1914	1915	1916	1917	1918	1919	1920	1921	1922	1923
12	21	22	21	36	27	16	16	15	11

 

D'Ancona asked his father-in-law Vito Volterra, a famous Italian mathematician, if there was a mathematical model that could explain the increase in predator fish during the World War I period. Within a couple of months, Volterra produced a series of models for the interaction of two or more species.

The data above do not show oscillations, but there is clearly a rise and fall of the percent of sharks and skates in the fish catch due to effects of the war. A slight modification of the predator prey model developed above and an equilibrium analysis can be used to explain the observed data. Volterra reasoned that the change in the relative frequency must be related to the changes in the fishing practices during the war. In particular, because of the dangers of fishing during wartime and because of the loss of fishermen who were required to fight in the war, there was a significant decline in the amount of fishing during the war. This needs to be included in the mathematical model for the interaction between the predatory fish and their prey fish.

Let F(t) be the food fish or prey fish and S(t) be the shark and skate population (less desirable catch in those times). The Lotka-Volterra predator-prey model, which includes fishing can be written:

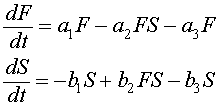
The terms with the coefficients a₁, a₂, b₁, and b₂ are the same as were developed for the predator-prey model for the lynx and hares above. There is another significant predator to both of these populations, human fishermen. The fishermen trolled for these fish primarily with nets that indiscriminately extracted both food fish and the predatory fish (though possibly at different rates). To model the effects of fishing, we add the terms a₃F and b₃S, where a₃ and b₃ reflect the intensity of fishing. These terms are appropriate as an approximation, since the fishing nets will sweep out a percentage of all fish in their paths that is proportional to the populations of fish in the region that is being fished.

Since the data that D'Ancona collected represent annual percentages of fish in the markets, one can assume that the populations of fish during that time are approximately in equilibrium. It can be shown (mathematically) that the average population about a cycle of the Lotka-Volterra model is its equilibrium value. Thus, if the fishing populations are cycling less than annually, the annual catch should reflect the equilibrium population. So this model is assuming a more rapid dynamics of the fish population than the lynx and hares above. If F_e and S_e represent the equilibrium populations of the food fish and sharks/skates populations respectively, then these equilibria are found by solving

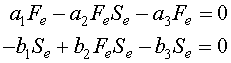
As before, these equations are factored to make solving them easy. The first equation is written

which implies that either F_e = 0 or a₁ - a₂S_e - a₃ = 0. Thus, the equilibria have either

F_e = 0 or .

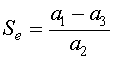Similarly, the second equation is factored to form the equation

which implies that either S_e = 0 or -b₁ + b₂F_e - b₃ = 0. Thus, we have possible equilibria at

S_e = 0 or .

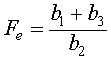Thus, as before, one of the equilibria is the trivial solution with neither species existing,

The other equilibrium satisfies

.

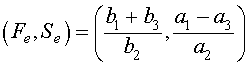which agrees with the equilibrium of the lynx-hare model above. This equilibrium value is fixed and independent of human interaction. It is determined solely by the ecological interactions of the fish and their predators, the sharks and skates. The human fishing activity is reflected in the parameters a₃ and b₃, which are both positive. As the level of fishing increases, these parameters increase. From the analysis above, we saw that the nonzero equilibrium is given by

The equilibrium value of the food fish, F_e, clearly increases as b₃ increases. In one respect, this makes sense because one would expect the food fish to benefit from the harvesting by humans of their natural predators in the Adriadic Sea. However, the model shows that human interference (at least when not too extreme) by harvesting the food fish, which is reflected in the constant a₃, does not appear in the formula for F_e, and so has no effect on the food fish equilibrium. This result is not so intuitive!

Similarly, the equilibrium value of the sharks and skates, S_e, clearly decreases as a₃ increases. This makes sense because the fisherman are in direct competition with the sharks and skates for this food source. However, again the model shows that human interference (at least when not too extreme) by harvesting the sharks and skates, which is reflected in the constant b₃, has no effect on the shark and skate equilibrium. Once again, this result is not so intuitive!

The data of D'Ancona agrees qualitatively with our equilibrium analysis. During World War I, the fishing fleets would be less likely to go out. This implies that the level of fishing decreases, so a₃ and b₃ decrease. Thus, the equilibrium value for the food fish decreases, while the equilibrium for the sharks and skates increases.The result appearing in the market data would be an increase in the percentage of shark and skates available, which is shown in the data. Because of this decrease in the level of fishing, the overall amount of fish products in the market would decrease, which is not shown in the data. There is insufficient data to obtain more than this gross qualitative overview of the effect of human fishing on the population dynamics. Detailed studies would be required to obtain more quantitative results and fit the six parameters in this system of differential equations.

References

[1] Lotka, A. J. 1920. Analytical note on certain rhythmic relations in organic systems, Proc. Natl. Acad. Sci. 6, 410-415.

[2] Lotka, A. J. 1925. Elements of Physical Biology. Baltimore: Williams & Wilkins Co.

[3] Volterra, V. 1926. Variazioni e fluttuazioni del numero d'individui in specie animali conviventi. Mem. R. Accad. Naz. dei Lincei. Ser. VI, vol. 2.