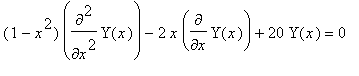
Runge-Kutta Procedure

We begin with a procedure from the text, which creates the classical Runge-Kutta method for solving a system of ordinary differential equations. This procedure uses both a for statement, which has the form

for i from start by change to finish

and a do statement, which has the form

do

statement

od:

The procedure contains several local variables, which are defined only inside the program.

> RKS := proc(f,x,y,h,N)

> local k1,k2,k3,k4,n;

> for n from 0 to N do

> k1 := h*f(x[n], y[n]);

> k2 := h*f(x[n]+h/2,y[n]+k1/2);

> k3 := h*f(x[n]+h/2,y[n]+k2/2);

> k4 := h*f(x[n]+h,y[n]+k3);

> y[n+1] := y[n] + (k1 + 2*k2 + 2*k3 + k4)/6;

> x[n+1] := x[n] + h:

> od:

> end:

Suppose we want to use this procedure to solve Legendre's equation

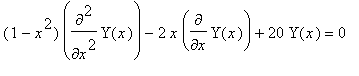
for 5 steps with h = 0.2, then compare the answer to the exact answer at t = 1.

> f := (x,y) -> [y[2], (2*x*y[2]-20*y[1])/(1-x^2)];

Suppose we start with the initial conditions y (0) = 1, y '(0) = 0.

> x[0] := 0; y[0] := [1, 0];

We implement the Runge-Kutta solver for 9 steps with stepsize 0.1. Note that the program goes to N +1. (This equation is singular at x = 1.)

> RKS(f, x, y, 0.1, 8);

> seq([x[k],y[k]], k = 0..9);
XY := [seq([x[k],y[k][1]], k = 0..9)]:

We would like to compare this answer to the solution of this differential equation, so next we use dsolve to find the actual solution.

> de := (1-x^2)*diff(Y(x),x,x)-2*x*diff(Y(x),x)+20*Y(x)=0;

> dsolve({de, Y(0)=1, D(Y)(0)=0}, Y(x));

> Y := unapply(rhs(%),x);

We can readily compare the actual solution to the numerical value computed above at t = 0.5 and 0.9.

> [Y(0.5),y[5][1]];abs((Y(0.5)-y[5][1])/Y(0.5));

> [Y(0.9),y[9][1]];abs((Y(0.9)-y[9][1])/Y(0.9));

Below we visualize the actual solution and the numerical solution.

> with(plots):

Warning, the name changecoords has been redefined

> P1 := plot([XY]): P2 := plot(Y(x), x = 0..0.9, color = BLUE):

> display({P1,P2});