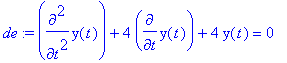
Solving Differential Equations

Maple uses a number techniques for solving differential equations, including exact methods, series techniques, and numerical solutions. First we find the general solution of a differential equation.

> de1 := diff(y(t),t$2) + 4*diff(y(t),t) + 4*y(t) = 0;

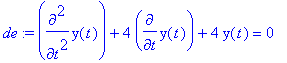
> dsolve(de1, y(t));

Next we solve and initial value problem.

> de2 := diff(y(t),t$2) + 4*diff(y(t),t) + 5*y(t) = 15*t^3;

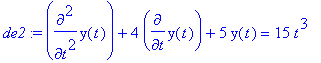
> dsolve({de2, y(0) = 5, D(y)(0) = -2}, y(t));

The equation below is Bessel's equation of second order, which has well known solutions known as Bessel's functions. We use Maple to show the series solution of this equation.

> de3 := t^2*diff(y(t),t$2) + t*diff(y(t),t) + (t^2-4)*y(t) = 0;

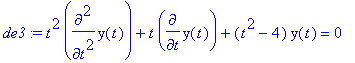
> dsolve(de3, y(t));

> dsolve(de3, y(t), series);

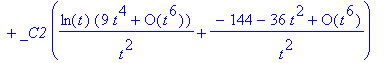
We can increase the number of terms generated by the series solution.

> Order := 12:

> dsolve(de3, y(t), series);

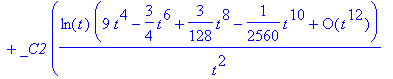
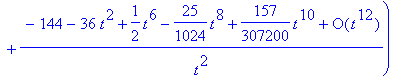
Maple can solve some systems of differential equations.

> sys := {diff(x(t),t) = 2*x(t) - y(t) - 2*z(t), diff(y(t),t) = x(t) + 2*y(t), diff(z(t),t) = 2*x(t) - z(t)};

> dsolve(sys, {x(t),y(t),z(t)});

Many differential equations cannot be solved exactly, but there are numerical methods to solve differential equations. The default method for Maple is the Runge-Kutta Fehlberg 45 method. We use the Lotka-Volterra model to demonstrate the numerical solver.

> LVx := diff(x(t),t) = x(t)*(1-y(t));
LVy := diff(y(t),t) = 0.3*y(t)*(x(t)-1);

> ff := dsolve({LVx, LVy, x(0)=0.2, y(0)=1},
{x(t),y(t)}, type=numeric, output=listprocedure);

> fx := subs(ff,x(t)): fy := subs(ff,y(t)):

Next we use numerical solution to generate a series of points, which are then graphed.

> LVsoln := [seq([fx(0.1*n),fy(0.1*n)], n = 0..200)]:

> plot(LVsoln, title=`Lotka-Volterra Model`, labels=[`prey`,`predator`], color=blue, thickness=2);