Introduction
The planetary motions are essentially described by ellipses although they may be slightly perturbed by the motion of the other "heavenly bodies". First, consider only the interaction between the sun's gravitational field and any given planet (or asteroid): we use a spherical coordinate system about the sun with coordinates:
![]()
We examine only the motion of r vs. theta and for the non-relativistic case, the equation of motion (for the Kepler orbits) is given by:
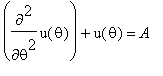
Where A is an expression in e , a , m , and mu - the reduced mass of the planet.
We take this opportunity to define precisely the meaning of these symbols and others used in this worksheet:
Symbol , Units, and Meaning
---------------------------------------------------------------------------------------
Gravitational constant. G=6.672*10^(-11) Newton-meters^2/Kg^2
Mass of the Sun. M = 1.99*10^30 Kg
orbit Eccentricity of Mercury e = 0.2056
semi-major axis of ellipse traced by Mercury's orbit a = 0.3871 A.U
Astronomical Unit for distance. A.U.=1.495*10^11 meters
speed of light. c =2.997925*10^8 meters/second
Period of Mercury's orbit. T = 0.2408 years
---------------------------------------------------------------------------------------
Now we see A is
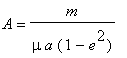
The reduced mass mu is defined as
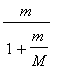
Since the mass of the sun is much larger than the planets m/mu is approximately 1. So A is approximately
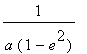
The solution to this equation is well known.
![]()
and this constant called e defines the eccentricity of the orbit. The above is determined when at theta = 0, u is at a maximum and r is a minimum. This corresponds to perihelion.
This is an oscillary solution with natural angular frequency of 1 and every 2 Pi rotation of the planet around the Sun returns u (and r) to its perihelion value.
However if we include the effects of other bodies, this causes perturbations in such a way that u(theta) does NOT quite return to it's initial value and thus the perihelion is displaced and the major axis of the ellipse starts moving at each revolution. In other words, the orbits starts precessing.
These effects are very small. The perihelion of Mercury, which shows the largest effect, was observed to move only about 574 sec of arc per century. Detailed calculations of the influence of the other planets on the motion of Mercury predict that the precession rate of the perihelion should be about 531 sec of arc per century.
This left a discrepancy of 43 sec which could not be accounted for! (using standard Newtonian mechanics).
>