Linear Analysis about Equilibria

One can determine a great deal about the behavior of a differential equation by examining the local behavior near an equilibrium. Let us find the Taylor series expansion near the equilibrium where both x and y are nonzero.

> coeq:=xyeq[4];

> cox := rhs(coeq[2]); coy := rhs(coeq[1]);

> taylor(f1(x,coy),x=cox);

> taylor(f1(cox,y),y=coy);

We want to compare the above computation with the one derived by computing the Jacobian matrix and evaluating at the equilibria. In addition, we find the eigenvalues and eigenvectors at all 4 equilibria.

> with(linalg):

Warning, the name adjoint has been redefined

Warning, the protected names norm and trace have been redefined and unprotected

> A := vector([f1(X,Y),f2(X,Y)]);

> J := jacobian(A, [X,Y]);

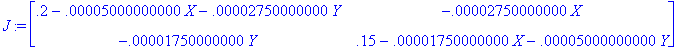
Analyze the differential equation near (0, 0).

> X := 0: Y := 0: J0 := J(0,0);

> eigenvects(J0);

This gives an unstable node , since both eigenvalues are positive.

Next analyze the coexistence equilibrium.

> X := cox: Y := coy: J0 := J(cox,coy);

> eigenvects(J0);

This gives a stable node , since both eigenvalues are negative.

> Plot2 := DEplot([dex,dey],[x(t),y(t)], t=0..70, x=6030..6120, y=1700..1800,[[x(0)=6030,y(0)=1700], [x(0)=6030,y(0)=1800], [x(0)=6120,y(0)=1700], [x(0)=6120,y(0)=1800]], arrows=MEDIUM, title=`Competition Model`, linecolor=t/50, color=CYAN):
Plot2;

The plot above shows the local behavior near the coexistence equilibrium.

Below is the equilibrium, where only species X exists.

> X := 8000: Y := 0: J0 := J(8000,0);

> eigenvects(J0);

This gives a saddle node , since the eigenvalues consists of a positive and negative eigenvalue.

Finally, we examine the Y species only equilibrium.

> X := 0: Y := 6000: J0 := J(0,6000);

> eigenvects(J0);

This gives a saddle node , since the eigenvalues consists of a positive and negative eigenvalue.

> Plot3 := DEplot([dex,dey],[x(t),y(t)], t=0..100, x=-100..100, y=5900..6100,[[x(0)=-10,y(0)=5900], [x(0)=-10,y(0)=6100], [x(0)=10,y(0)=5900], [x(0)=10,y(0)=6100]], arrows=MEDIUM, title=`Competition Model`, linecolor=t/50, color=CYAN):
Plot3;