The Linear Algebra Package

Maple 6 has two packages for doing linear algebra-- LinearAlgebra, which is new, and linalg.

The new package improves on the older linalg package in many ways. We'll look at some of the features of the new package. A fundamental difference is that Vectors and Matrices are stored as rtables rather than tables. This means that accessing

First, defining a Vector or Matrix can be done in very many ways (note the capital letter means Maple will use Linear Algebra not linalg). We'll just look at a couple.

Specifying just the dimension gives you an object with all 0's,.

> Vector(2);

You can also specify the entries in several ways:

> A:= Vector(1..3, 5); A[2];

> f:= (j) -> x^(j-1); Vector(3,f);

> g:= k -> k*(k-1); Vector(3,g);

There is an option to specify a row Vector. The example also shows two other things 1) you can just spell out the entries, you don't have to say the dimensions, 2) your entries can be numbers, variables, and functions.

> C := Vector[row]([3,x^2,g]);

The default for a random Vector is integer entries between -99 and 99. You can also specify a random number generator. There are other options too: e.g. specify the density, specify the shape.

> RanVec := LinearAlgebra[RandomVector];

> B := RanVec(3);

> rn := rand(1..10^6);

> RanVec(10, generator = rn, density = .5);

Arithmetic operations are easy to write. Recall our Vectors A, B..

> A; B; A+5*B;

Matrtix multiplications is also easy (and the LinearAlgebra package is not required).

> C; A.C;

If you want to apply a function to each term use the map command.

> map(exp, A);

For Matrices the same techniques apply.

Additional constructors for matrices are Identity Matrix, ScalarMatrix, DiagonalMatrix,

BandMatrix and many others.

> M := LinearAlgebra[DiagonalMatrix]([5,3,4]);

>

Multiplication of a Matrix and Vector and Matrix inversion are easy:

> M.A; M^(-1);

Let's get the whole package now.

> with(LinearAlgebra);

You can specify the entries of a Matrix as follows:

> N := <<2,3,4>|<1,2,3>|<5,0,7>>;

Just to prove there is a difference between matrix and Matrix.

> type(M,matrix); type(M,Matrix);

Now, to solve a system.

>

> LinearSolve(N,A);

New Matrices from old:

> P := <N,N>; Q := <N|N>;

Solving the following linear system gives a three dimensional space.

> LinearSolve(Q,A);

> Q.<1,0,0,4,-5,0>; Q.<0,1,0,5,-6,0>; Q.<0,0,1,5,-5,-1>;

Eigenvectors gives you a vector with the Eigenvalues, followed by a matrix with the corresponding Eigenvectors.

> H := evalf(Eigenvectors(N));

> H[1];

To select the Eigenvector, select the second element of the list H then select the first column.

> K := H[2];

> K[1..3,1];

> h:=CharacteristicPolynomial(N,x);

> solve(h,x);

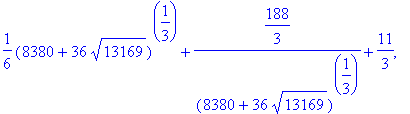
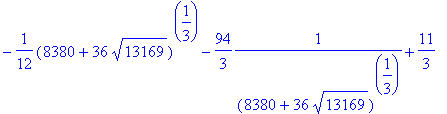
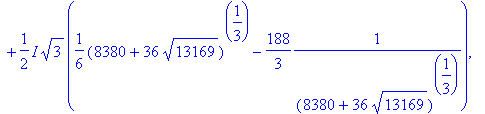
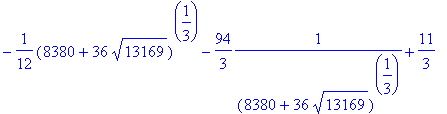
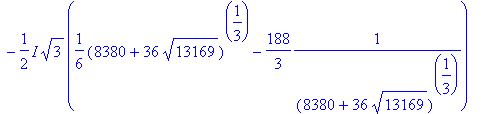
> plots[matrixplot](P);